10.3: Test of Independence

41

Test of Independence

jkesler

[latexpage]

Tests of independence involve using a contingency table of observed (data) values.

The test statistic for a test of independence is similar to that of a goodness-of-fit test:

$$\sum_{(i,j)} \frac{(O-E)^2}{E}$$

where:

• O = observed values
• E = expected values
• i = the number of rows in the table
• j = the number of columns in the table

There are $i\cdot j$ terms of the form $\frac{(O-E)^2}{E}$, and these resulting values are sometimes called the residuals.

A test of independence determines whether two factors are independent or not. You first encountered the term independence in Probability Topics. As a review, consider the following example.

Note

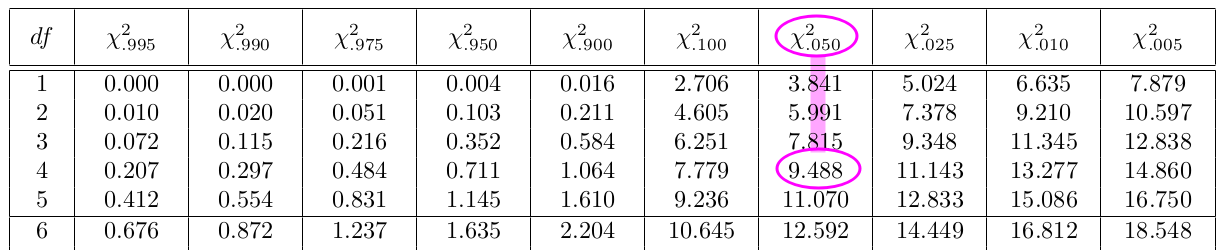
The expected value for each cell needs to be at least five in order for you to use this test.

Example 10.5

Suppose A = a speeding violation in the last year and B = a cell phone user while driving. If A and B are independent then P(A AND B) = P(A)P(B). A AND B is the event that a driver received a speeding violation last year and also used a cell phone while driving. Suppose, in a study of drivers who received speeding violations in the last year, and who used cell phone while driving, that 755 people were surveyed. Out of the 755, 70 had a speeding violation and 685 did not; 305 used cell phones while driving and 450 did not.

Let y = expected number of drivers who used a cell phone while driving and received speeding violations.

If A and B are independent, then P(A AND B) = P(A)P(B). By substitution,

$\frac{y}{755} = \left( \frac{70}{755} \right) \left( \frac{305}{755} \right)$

Solve for $y$: $y=\frac{(70)(305)}{755}=28.3$

About 28 people from the sample are expected to use cell phones while driving and to receive speeding violations.

In a test of independence, we state the null and alternative hypotheses in words. Since the contingency table consists of two factors, the null hypothesis states that the factors are independent and the alternative hypothesis states that they are not independent (dependent). If we do a test of independence using the example, then the null hypothesis is:

H₀: Being a cell phone user while driving and receiving a speeding violation are independent events.

If the null hypothesis were true, we would expect about 28 people to use cell phones while driving and to receive a speeding violation.

The test of independence is always right-tailed because of the calculation of the test statistic. If the expected and observed values are not close together, then the test statistic is very large and way out in the right tail of the chi-square curve, as it is in a goodness-of-fit.

The number of degrees of freedom for the test of independence is:

df = (number of columns – 1)(number of rows – 1)

The following formula calculates the expected number (E):

$$E=\frac{(\text{row total})(\text{column total})}{\text{total number surveyed}}$$

Try It 10.5

A sample of 300 students is taken. Of the students surveyed, 50 were music students, while 250 were not. Ninety-seven were on the honor roll, while 203 were not. If we assume being a music student and being on the honor roll are independent events, what is the expected number of music students who are also on the honor roll?

Example 10.6

In a volunteer group, adults 21 and older volunteer from one to nine hours each week to spend time with a disabled senior citizen. The program recruits among community college students, four-year college students, and nonstudents. In Table 10.15 is a sample of the adult volunteers and the number of hours they volunteer per week.

Type of Volunteer	1–3 Hours	4–6 Hours	7–9 Hours	Row Total
Community College Students	111	96	48	255
Four-Year College Students	96	133	61	290
Nonstudents	91	150	53	294
Column Total	298	379	162	839

Table 10.15Number of Hours Worked Per Week by Volunteer Type (Observed) The table contains observed (O) values (data).

Is the number of hours volunteered independent of the type of volunteer?

Solution 10.6

The observed table and the question at the end of the problem, “Is the number of hours volunteered independent of the type of volunteer?” tell you this is a test of independence. The two factors are number of hours volunteered and type of volunteer. This test is always right-tailed.

H₀: The number of hours volunteered is independent of the type of volunteer.

H₁: The number of hours volunteered is dependent on the type of volunteer.

Calculate E, the Expected Values

The expected results are in Table 10.16. Each entry in the table is calculated using the formula

$$E=\frac{(\text{row total})(\text{column total})}{\text{total number surveyed}}$$

The table contains expected (E) values (data).

Type of Volunteer	1-3 Hours	4-6 Hours	7-9 Hours
Community College Students	90.57	115.19	49.24
Four-Year College Students	103.00	131.00	56.00
Nonstudents	104.42	132.81	56.77

Table 10.16Number of Hours Worked Per Week by Volunteer Type (Expected)

For example, the calculation for the expected frequency for the top left cell is

$$E=\frac{(\text{row total})(\text{column total})}{\text{total number surveyed}}=\frac{(255)(298)}{839}=90.57$$

Create the $O-E$ table:

To create this table, simply subtract the values in each cell of the Expected table from the values in each cell of the original Observed table.

The table contains observed (O) – expected (E) values.

Type of Volunteer	1-3 Hours	4-6 Hours	7-9 Hours
Community College Students	20.43	-19.19	-1.24
Four-Year College Students	-7	2	5
Nonstudents	-13.42	17.19	-3.77

Table 10.16aObserved minus Expected Number of Hours Worked Per Week by Volunteer Type

Create the $\frac{(O-E)^2}{E}$ table:

To create this table, square the values in each cell in the above $O-E$ table, and then divide each cell by the corresponding expected value in the $E$ expected value table.

The table contains the residuals $\frac{(O-E)^2}{E}$

Type of Volunteer	1-3 Hours	4-6 Hours	7-9 Hours
Community College Students	4.608	3.197	0.031
Four-Year College Students	0.476	0.031	0.446
Nonstudents	1.725	2.225	0.25

Table 10.16bResiduals of Number of Hours Worked Per Week by Volunteer Type

 

Calculate the test statistic:

Add all values together in the the above table $\frac{(O-E)^2}{E}$

χ² = 12.99

Distribution for the test:

$\chi_4^2$

df = (3 columns – 1)(3 rows – 1) = (2)(2) = 4

Graph:

Figure 10.7

Probability statement:

We can use the CHISQ.DIST.RT as follows:

=CHISQ.DIST.RT(12.99,4)

This gives us p-value=P(χ² > 12.99) = 0.0113

Compare α and the p-value: Since no α is given, assume α = 0.05. p-value = 0.0113. α > p-value.

Make a decision: Since α > p-value, reject H₀. This means that the factors are not independent.

Conclusion: At a 5% level of significance, from the data, there is sufficient evidence to conclude that the number of hours volunteered and the type of volunteer are dependent on one another.

For the example in Table 10.15, if there had been another type of volunteer, teenagers, what would the degrees of freedom be

Critical Value Method

If we were asked to calculate the critical value (instead of a p-value), we could use the significance level 0.05, the degrees of freedom 4, and the Google Sheets function CHISQ.INV.RT

=CHISQ.INV.RT(0.05,4)

We find the critical value to be 9.488; comparing this to our test statistic 12.99, we reject H₀ since our test statistic is larger. Note that this is (and should always be) the same conclusion as using the p-value.

Using the Chi Square Distribution Table

p-value Method

To use the Chi2 Distribution Table to find a p-value range, look in the degrees of freedom row, 4 in this example. Find which two numbers “sandwich” your test statistic, 12.99.

Our test statistic is between 11.143 and 13.277, so following those two columns up, we see our p-value is between 0.01 and 0.025

0.01 < p-value < 0.025

With this range, we can say for certain our p-value is less than the significance level 0.05, so we reject H₀

 

Critical Value Method

To use the Chi2 Distribution Table to find a critical value, find the 0.05 entry in the top row, go down to the df row 4. We get 9.488 as the critical value. Our test statistic 12.99 is larger, so we reject H₀.

 

Try It 10.6

The Bureau of Labor Statistics gathers data about employment in the United States. A sample is taken to calculate the number of U.S. citizens working in one of several industry sectors over time. Table 10.17 shows the results:

Industry Sector	2000	2010	2020	Total
Nonagriculture wage and salary	13,243	13,044	15,018	41,305
Goods-producing, excluding agriculture	2,457	1,771	1,950	6,178
Services-providing	10,786	11,273	13,068	35,127
Agriculture, forestry, fishing, and hunting	240	214	201	655
Nonagriculture self-employed and unpaid family worker	931	894	972	2,797
Secondary wage and salary jobs in agriculture and private household industries	14	11	11	36
Secondary jobs as a self-employed or unpaid family worker	196	144	152	492
Total	27,867	27,351	31,372	86,590

Table 10.17

We want to know if the change in the number of jobs is independent of the change in years. State the null and alternative hypotheses and the degrees of freedom.

Example 10.7

De Anza College is interested in the relationship between anxiety level and the need to succeed in school. A random sample of 400 students took a test that measured anxiety level and need to succeed in school. Table 10.18 shows the results. De Anza College wants to know if anxiety level and need to succeed in school are independent events.

Need to Succeed in School	High Anxiety	Med-high Anxiety	Medium Anxiety	Med-low Anxiety	Low Anxiety	Row Total
High Need	35	42	53	15	10	155
Medium Need	18	48	63	33	31	193
Low Need	4	5	11	15	17	52
Column Total	57	95	127	63	58	400

Table 10.18Need to Succeed in School vs. Anxiety Level

1. How many high anxiety level students are expected to have a high need to succeed in school?
2. If the two variables are independent, how many students do you expect to have a low need to succeed in school and a med-low level of anxiety?
3. $E=\frac{(\text{row total})(\text{column total})}{\text{total number surveyed}}=$______
4. The expected number of students who have a med-low anxiety level and a low need to succeed in school is about ________.

Solution 10.7

1. The column total for a high anxiety level is 57. The row total for high need to succeed in school is 155. The sample size or total surveyed is 400.$E=\frac{(\text{row total})(\text{column total})}{\text{total number surveyed}}=\frac{155.57}{400}=22.09$The expected number of students who have a high anxiety level and a high need to succeed in school is about 22.

2. The column total for a med-low anxiety level is 63. The row total for a low need to succeed in school is 52. The sample size or total surveyed is 400.

3. $E=\frac{(\text{row total})(\text{column total})}{\text{total number surveyed}}=8.19$

4. 8

Try It 10.7

Refer back to the information in Try It. How many service providing jobs are there expected to be in 2020? How many nonagriculture wage and salary jobs are there expected to be in 2020?