5.3: Probability Computations for General Normal Random Variables
- Page ID
- 526
- To learn how to compute probabilities related to any normal random variable.
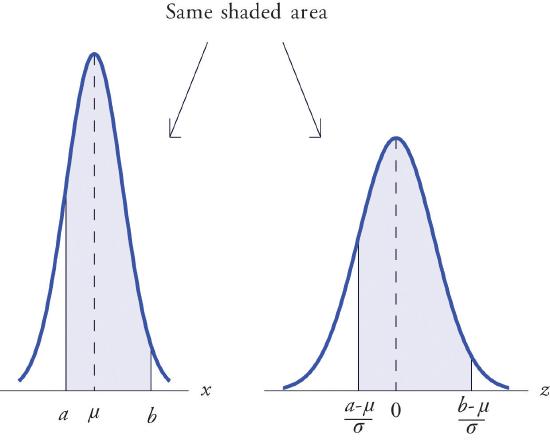
If \(X\) is any normally distributed normal random variable then Figure \(\PageIndex{1}\) can also be used to compute a probability of the form \(P(a<X<b)\) by means of the following equality.
If \(X\) is a normally distributed random variable with mean \(\mu\) and standard deviation \(\sigma\), then \[P(a<X<b)=P\left ( \frac{a-\mu }{\sigma }<Z<\frac{b-\mu }{\sigma } \right ) \nonumber \] where \(Z\) denotes a standard normal random variable. \(a\) can be any decimal number or \(-\infty\); \(b\) can be any decimal number or \(\infty\).


The new endpoints \(\frac{(a-\mu )}{\sigma }\) and \(\frac{(b-\mu )}{\sigma }\) are the \(z\)-scores of \(a\) and \(b\) as defined in Chapter 2.
Figure \(\PageIndex{2}\) illustrates the meaning of the equality geometrically: the two shaded regions, one under the density curve for \(X\) and the other under the density curve for \(Z\), have the same area. Instead of drawing both bell curves, though, we will always draw a single generic bell-shaped curve with both an \(x\)-axis and a \(z\)-axis below it.
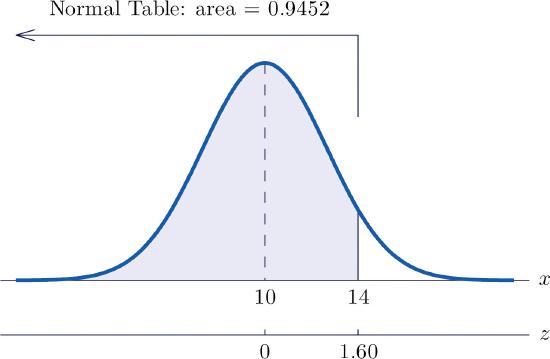
Let \(X\) be a normal random variable with mean \(\mu =10\) and standard deviation \(\sigma =2.5\). Compute the following probabilities.
- \(P(X<14)\).
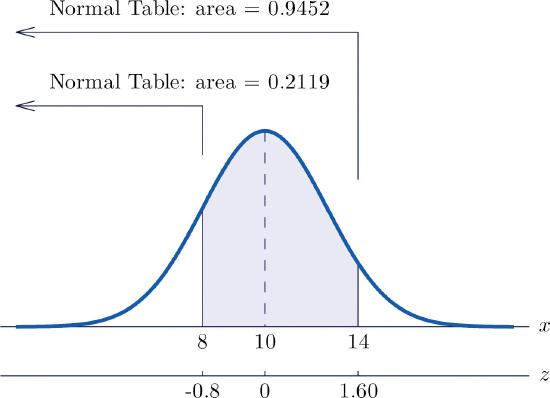
- \(P(8<X<14)\).
Solution
- See Figure \(\PageIndex{3}\) "Probability Computation for a General Normal Random Variable". \[\begin{align*} P(X<14) &= P\left ( Z<\frac{14-\mu }{\sigma } \right )\\ &= P\left ( Z<\frac{14-10}{2.5} \right )\\ &= P(Z<1.60)\\ &= 0.9452 \end{align*} \nonumber \]
- See Figure \(\PageIndex{4}\) "Probability Computation for a General Normal Random Variable". \[\begin{align*} P(8<X<14) &= P\left ( \frac{8-10}{2.5}<Z<\frac{14-10}{2.5} \right )\\ &= P\left ( -0.80<Z<1.60 \right )\\ &= 0.9452-0.2119\\ &= 0.7333 \end{align*} \nonumber \]
The lifetimes of the tread of a certain automobile tire are normally distributed with mean \(37,500\) miles and standard deviation \(4,500\) miles. Find the probability that the tread life of a randomly selected tire will be between \(30,000\) and \(40,000\) miles.
Solution
Let \(X\) denote the tread life of a randomly selected tire. To make the numbers easier to work with we will choose thousands of miles as the units. Thus \(\mu =37.5,\; \sigma =4.5\), and the problem is to compute \(P(30<X<40)\). Figure \(\PageIndex{5}\) "Probability Computation for Tire Tread Wear" illustrates the following computation:
\[\begin{align*} P(30<X<40) &= P\left ( \frac{30-\mu }{\sigma }<Z<\frac{40-\mu }{\sigma } \right )\\ &= P\left ( \frac{30-37.5}{4.5}<Z<\frac{40-37.5}{4.5} \right )\\ &= P\left ( -1.67<Z<0.56\right )\\ &= 0.7123-0.0475\\ &= 0.6648 \end{align*} \nonumber \]
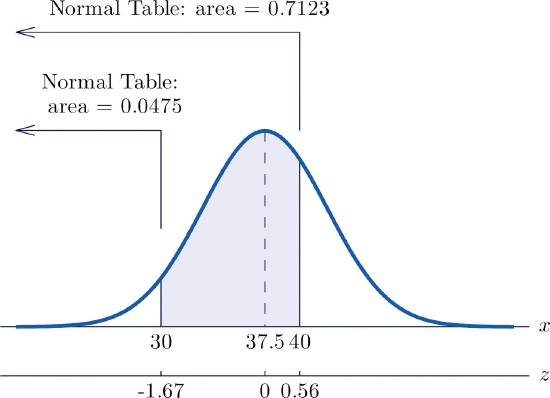
Note that the two \(z\)-scores were rounded to two decimal places in order to use Figure \(\PageIndex{1}\) "Cumulative Normal Probability".
Scores on a standardized college entrance examination (CEE) are normally distributed with mean \(510\) and standard deviation \(60\). A selective university considers for admission only applicants with CEE scores over \(650\). Find percentage of all individuals who took the CEE who meet the university's CEE requirement for consideration for admission.
Solution
Let \(X\) denote the score made on the CEE by a randomly selected individual. Then \(X\) is normally distributed with mean \(510\) and standard deviation \(60\). The probability that \(X\) lie in a particular interval is the same as the proportion of all exam scores that lie in that interval. Thus the solution to the problem is \(P(X>650)\), expressed as a percentage. Figure \(\PageIndex{6}\) "Probability Computation for Exam Scores" illustrates the following computation:
\[\begin{align*} P(X>650) &= P\left ( Z>\frac{650-\mu }{\sigma } \right )\\ &= P\left ( Z>\frac{650-510}{60} \right )\\ &= P(Z>2.33)\\ &= 1-0.9901\\ &= 0.0099 \end{align*} \nonumber \]
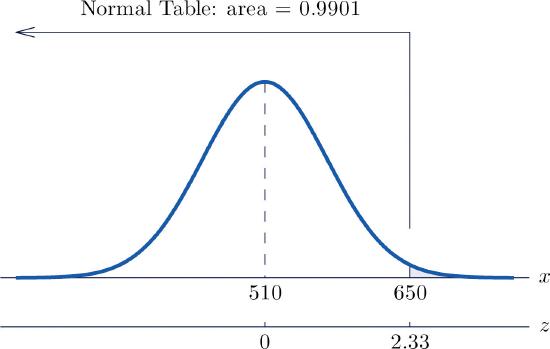
The proportion of all CEE scores that exceed \(650\) is \(0.0099\), hence \(0.99\%\) or about \(1\%\) do.
key takeaway
- Probabilities for a general normal random variable are computed using Figure \(\PageIndex{1}\) after converting \(x\)-values to \(z\)-scores.


