10.E: Estimation (Exercises)
- Page ID
- 2636
You may want to use the Analysis Lab and various calculators for some of these exercises.
Calculators:
- Inverse t Distribution: Finds t for a confidence interval.
- t Distribution: Computes areas of the t distribution.
- Fisher's r to z': Computes transformations in both directions.
- Inverse Normal Distribution: Use for confidence intervals.
General Questions
Q1
When would the mean grade in a class on a final exam be considered a statistic? When would it be considered a parameter? (relevant section)
Q2
Define bias in terms of expected value. (relevant section)
Q3
Is it possible for a statistic to be unbiased yet very imprecise? How about being very accurate but biased? (relevant section)
Q4
Why is a \(99\%\) confidence interval wider than a \(95\%\) confidence interval? (relevant section & relevant section)
Q5
When you construct a \(95\%\) confidence interval, what are you \(95\%\) confident about? (relevant section)
Q6
What is the difference in the computation of a confidence interval between cases in which you know the population standard deviation and cases in which you have to estimate it? (relevant section & relevant section)
Q7
Assume a researcher found that the correlation between a test he or she developed and job performance was \(0.55\) in a study of \(28\) employees. If correlations under \(0.35\) are considered unacceptable, would you have any reservations about using this test to screen job applicants? (relevant section)
Q8
What is the effect of sample size on the width of a confidence interval? (relevant section & relevant section)
Q9
How does the \(t\) distribution compare with the normal distribution? How does this difference affect the size of confidence intervals constructed using \(z\) relative to those constructed using \(t\)? Does sample size make a difference? (relevant section)
Q10
The effectiveness of a blood-pressure drug is being investigated. How might an experimenter demonstrate that, on average, the reduction in systolic blood pressure is \(20\) or more? (relevant section & relevant section)
Q11
A population is known to be normally distributed with a standard deviation of \(2.8\).
- Compute the \(95\%\) confidence interval on the mean based on the following sample of nine: \(8, 9, 10, 13, 14, 16, 17, 20, 21\).
- Now compute the \(99\%\) confidence interval using the same data. (relevant section)
Q12
A person claims to be able to predict the outcome of flipping a coin. This person is correct \(16/25\) times. Compute the \(95\%\) confidence interval on the proportion of times this person can predict coin flips correctly. What conclusion can you draw about this test of his ability to predict the future? (relevant section)
Q13
What does it mean that the variance (computed by dividing by \(N\)) is a biased statistic? (relevant section)
Q14
A confidence interval for the population mean computed from an \(N\) of \(16\) ranges from \(12\) to \(28\). A new sample of \(36\) observations is going to be taken. You can't know in advance exactly what the confidence interval will be because it depends on the random sample. Even so, you should have some idea of what it will be. Give your best estimation. (relevant section)
Q15
You take a sample of \(22\) from a population of test scores, and the mean of your sample is \(60\).
- You know the standard deviation of the population is \(10\). What is the \(99\%\) confidence interval on the population mean.
- Now assume that you do not know the population standard deviation, but the standard deviation in your sample is \(10\). What is the \(99\%\) confidence interval on the mean now? (relevant section)
Q16
You read about a survey in a newspaper and find that \(70\%\) of the \(250\) people sampled prefer Candidate \(A\). You are surprised by this survey because you thought that more like \(50\%\) of the population preferred this candidate. Based on this sample, is \(50\%\) a possible population proportion? Compute the \(95\%\) confidence interval to be sure. (relevant section)
Q17
Heights for teenage boys and girls were calculated. The mean height for the sample of \(12\) boys was \(174\) cm and the variance was \(62\). For the sample of \(12\) girls, the mean was \(166\) cm and the variance was \(65\).
- What is the \(95\%\) confidence interval on the difference between population means?
- What is the \(99\%\) confidence interval on the difference between population means?
- Do you think the mean difference in the population could be about \(5\)? Why or why not? (relevant section)
Q18
You were interested in how long the average psychology major at your college studies per night, so you asked \(10\) psychology majors to tell you the amount they study. They told you the following times: \(2, 1.5, 3, 2, 3.5, 1, 0.5, 3, 2, 4\).
- Find the \(95\%\) confidence interval on the population mean.
- Find the \(90\%\) confidence interval on the population mean. (relevant section)
Q19
True/false: As the sample size gets larger, the probability that the confidence interval will contain the population mean gets higher. (relevant section & relevant section)
Q20
True/false: You have a sample of \(9\) men and a sample of \(8\) women. The degrees of freedom for the \(t\) value in your confidence interval on the difference between means is \(16\). (relevant section & relevant section)
Q21
True/false: Greek letters are used for statistics as opposed to parameters. (relevant section)
Q22
True/false: In order to construct a confidence interval on the difference between means, you need to assume that the populations have the same variance and are both normally distributed. (relevant section)
Q23
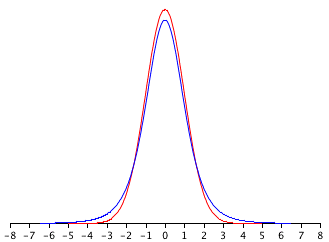
True/false: The red distribution represents the \(t\) distribution and the blue distribution represents the normal distribution. (relevant section)
Questions from Case Studies
The following questions are from the Angry Moods (AM) case study.
Q24
(AM#6c) Is there a difference in how much males and females use aggressive behavior to improve an angry mood? For the "Anger-Out" scores, compute a \(99\%\) confidence interval on the difference between gender means. (relevant section)
Q25
(AM#10) Calculate the \(95\%\) confidence interval for the difference between the mean Anger-In score for the athletes and non-athletes. What can you conclude? (relevant section)
Q26
Find the \(95\%\) confidence interval on the population correlation between the Anger-Out and Control-Out scores. (relevant section)
The following questions are from the Flatulence (F) case study.
Q27
(F#8) Compare men and women on the variable "perday." Compute the \(95\%\) confidence interval on the difference between means. (relevant section)
Q28
(F#10) What is the \(95\%\) confidence interval of the mean time people wait before farting in front of a romantic partner. (relevant section)
The following questions use data from the Animal Research (AR) case study.
Q29
(AR#3) What percentage of the women studied in this sample strongly agreed (gave a rating of \(7\)) that using animals for research is wrong?
Q30
Use the proportion you computed in #29. Compute the \(95\%\) confidence interval on the population proportion of women who strongly agree that animal research is wrong. (relevant section)
Q31
Compute a \(95\%\) confidence interval on the difference between the gender means with respect to their beliefs that animal research is wrong. (relevant section)
The following question is from the ADHD Treatment (AT) case study.
Q32
(AT#8) What is the correlation between the participants' correct number of responses after taking the placebo and their correct number of responses after taking \(0.60\) mg/kg of MPH? Compute the \(95\%\) confidence interval on the population correlation. (relevant section)
The following question is from the Weapons and Aggression (WA) case study.
Q33
(WA#4) Recall that the hypothesis is that a person can name an aggressive word more quickly if it is preceded by a weapon word prime than if it is preceded by a neutral word prime. The first step in testing this hypothesis is to compute the difference between
- the naming time of aggressive words when preceded by a neutral word prime and
- the naming time of aggressive words when preceded by a weapon word prime separately for each of the \(32\) participants. That is, compute an \(- aw\) for each participant.
- Would the hypothesis of this study be supported if the difference were positive or if it were negative?
- What is the mean of this difference score? (relevant section)
- What is the standard deviation of this difference score? (relevant section)
- What is the 95% confidence interval of the mean difference score? (relevant section)
- What does the confidence interval computed in (d) say about the hypothesis.
The following question is from the Diet and Health (WA) case study.
Q34
Compute a \(95\%\) confidence interval on the proportion of people who are healthy on the AHA diet.
| Cancers | Deaths | Nonfatal illness | Healthy | Total | |
| AHA |
The following questions are from (reproduced with permission)  Visit the site
Visit the site
Q35
Suppose that you take a random sample of \(10,000\) Americans and find that \(1,111\) are left-handed. You perform a test of significance to assess whether the sample data provide evidence that more than \(10\%\) of all Americans are left-handed, and you calculate a test statistic of \(3.70\) and a \(p\)-value of \(0.0001\). Furthermore, you calculate a \(99\%\) confidence interval for the proportion of left-handers in America to be \((0.103,0.119)\). Consider the following statements: The sample provides strong evidence that more than \(10\%\) of all Americans are left-handed. The sample provides evidence that the proportion of left-handers in America is much larger than \(10\%\). Which of these two statements is the more appropriate conclusion to draw? Explain your answer based on the results of the significance test and confidence interval.
Q36
A student wanted to study the ages of couples applying for marriage licenses in his county. He studied a sample of \(94\) marriage licenses and found that in \(67\) cases the husband was older than the wife. Do the sample data provide strong evidence that the husband is usually older than the wife among couples applying for marriage licenses in that county? Explain briefly and justify your answer.
Q37
Imagine that there are \(100\) different researchers each studying the sleeping habits of college freshmen. Each researcher takes a random sample of size \(50\) from the same population of freshmen. Each researcher is trying to estimate the mean hours of sleep that freshmen get at night, and each one constructs a \(95\%\) confidence interval for the mean. Approximately how many of these \(100\) confidence intervals will NOT capture the true mean?
- None
- \(1\) or \(2\)
- \(3\) to \(7\)
- about half
- \(95\) to \(100\)
- other
Selected Answers
S11
- \((12.39, 16.05)\)
S12
\((0.43, 0.85)\)
S15
- \((53.96, 66.04)\)
S17
- \((1.25, 14.75)\)
S18
- \((1.45, 3.05)\)
S26
\((-0.713, -0.414)\)
S27
\((-0.98, 3.09)\)
S29
\(41\%\)
S33
- \(7.16\)


