10.7: Confidence Interval for Mean
- Page ID
- 2627
Learning Objectives
- Use the inverse normal distribution calculator to find the value of \(z\) to use for a confidence interval
- Compute a confidence interval on the mean when \(\sigma\) is known
- Determine whether to use a \(t\) distribution or a normal distribution
- Compute a confidence interval on the mean when \(\sigma\) is estimated
When you compute a confidence interval on the mean, you compute the mean of a sample in order to estimate the mean of the population. Clearly, if you already knew the population mean, there would be no need for a confidence interval. However, to explain how confidence intervals are constructed, we are going to work backwards and begin by assuming characteristics of the population. Then we will show how sample data can be used to construct a confidence interval.
Assume that the weights of \(10\)-year-old children are normally distributed with a mean of \(90\) and a standard deviation of \(36\). What is the sampling distribution of the mean for a sample size of \(9\)? Recall from the section on the sampling distribution of the mean that the mean of the sampling distribution is \(\mu\) and the standard error of the mean is
\[\sigma _M=\frac{\sigma }{\sqrt{N}}\]
For the present example, the sampling distribution of the mean has a mean of \(90\) and a standard deviation of \(36/3 = 12\). Note that the standard deviation of a sampling distribution is its standard error. Figure \(\PageIndex{1}\) shows this distribution. The shaded area represents the middle \(95\%\) of the distribution and stretches from \(66.48\) to \(113.52\). These limits were computed by adding and subtracting \(1.96\) standard deviations to/from the mean of \(90\) as follows:
\[90 - (1.96)(12) = 66.48\]
\[ 90 + (1.96)(12) = 113.52\]
The value of \(1.96\) is based on the fact that \(95\%\) of the area of a normal distribution is within \(1.96\) standard deviations of the mean; \(12\) is the standard error of the mean.
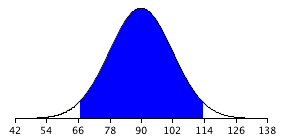
Figure \(\PageIndex{1}\) shows that \(95\%\) of the means are no more than \(23.52\) units (\(1.96\) standard deviations) from the mean of \(90\). Now consider the probability that a sample mean computed in a random sample is within \(23.52\) units of the population mean of \(90\). Since \(95\%\) of the distribution is within \(23.52\) of \(90\), the probability that the mean from any given sample will be within \(23.52\) of \(90\) is \(0.95\). This means that if we repeatedly compute the mean (\(M\)) from a sample, and create an interval ranging from \(M - 23.52\) to \(M + 23.52\), this interval will contain the population mean \(95\%\) of the time. In general, you compute the \(95\%\) confidence interval for the mean with the following formula:
\[\text{Lower limit} = M - Z_{0.95}\sigma _M\]
\[\text{Upper limit} = M + Z_{0.95}\sigma _M\]
where \(Z_{0.95}\) is the number of standard deviations extending from the mean of a normal distribution required to contain \(0.95\) of the area and \(\sigma _M\) is the standard error of the mean.
If you look closely at this formula for a confidence interval, you will notice that you need to know the standard deviation (\(\sigma\)) in order to estimate the mean. This may sound unrealistic, and it is. However, computing a confidence interval when \(\sigma\) is known is easier than when \(\sigma\) has to be estimated, and serves a pedagogical purpose. Later in this section we will show how to compute a confidence interval for the mean when \(\sigma\) has to be estimated.
Suppose the following five numbers were sampled from a normal distribution with a standard deviation of \(2.5: 2, 3, 5, 6,\; and\; 9\). To compute the \(95\%\) confidence interval, start by computing the mean and standard error:
\[M = \frac{2 + 3 + 5 + 6 + 9}{5} = 5\]
\[\sigma _M=\frac{2.5}{\sqrt{5}}=1.118\]
\(Z_{0.95}\) can be found using the normal distribution calculator and specifying that the shaded area is \(0.95\) and indicating that you want the area to be between the cutoff points. As shown in Figure \(\PageIndex{2}\), the value is \(1.96\). If you had wanted to compute the \(99\%\) confidence interval, you would have set the shaded area to \(0.99\) and the result would have been \(2.58\).
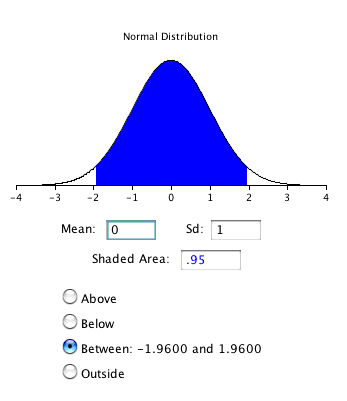
The confidence interval can then be computed as follows:
\[\text{Lower limit} = 5 - (1.96)(1.118)= 2.81\]
\[\text{Upper limit} = 5 + (1.96)(1.118)= 7.19\]
You should use the \(t\) distribution rather than the normal distribution when the variance is not known and has to be estimated from sample data. When the sample size is large, say \(100\) or above, the t distribution is very similar to the standard normal distribution. However, with smaller sample sizes, the \(t\) distribution is leptokurtic, which means it has relatively more scores in its tails than does the normal distribution. As a result, you have to extend farther from the mean to contain a given proportion of the area. Recall that with a normal distribution, \(95\%\) of the distribution is within \(1.96\) standard deviations of the mean. Using the \(t\) distribution, if you have a sample size of only \(5\), \(95\%\) of the area is within \(2.78\) standard deviations of the mean. Therefore, the standard error of the mean would be multiplied by \(2.78\) rather than \(1.96\).
The values of \(t\) to be used in a confidence interval can be looked up in a table of the \(t\) distribution. A small version of such a table is shown in Table \(\PageIndex{1}\). The first column, \(df\), stands for degrees of freedom, and for confidence intervals on the mean, \(df\) is equal to \(N - 1\), where \(N\) is the sample size.
| df | 0.95 | 0.99 |
|---|---|---|
| 2 | 4.303 | 9.925 |
| 3 | 3.182 | 5.841 |
| 4 | 2.776 | 4.604 |
| 5 | 2.571 | 4.032 |
| 8 | 2.306 | 3.355 |
| 10 | 2.228 | 3.169 |
| 20 | 2.086 | 2.845 |
| 50 | 2.009 | 2.678 |
| 100 | 1.984 | 2.626 |
You can also use the "inverse t distribution" calculator to find the \(t\) values to use in confidence intervals. You will learn more about the \(t\) distribution in the next section.
Assume that the following five numbers are sampled from a normal distribution: \(2, 3, 5, 6,\; and\; 9\) and that the standard deviation is not known. The first steps are to compute the sample mean and variance:
\[M=5\; \text{and}\; S^2=7.5\]
The next step is to estimate the standard error of the mean. If we knew the population variance, we could use the following formula:
\[\sigma _M=\frac{\sigma }{\sqrt{N}}\]
Instead we compute an estimate of the standard error (\(s_M\)):
\[s _M=\frac{s}{\sqrt{N}}=1.225\]
The next step is to find the value of \(t\). As you can see from Table \(\PageIndex{1}\), the value for the \(95\%\) interval for \(df = N - 1 = 4\) is \(2.776\). The confidence interval is then computed just as it is when \(\sigma _M\). The only differences are that \(s_M\) and t rather than \(\sigma _M\) and \(Z\) are used.
\[\text{Lower limit} = 5 - (2.776)(1.225) = 1.60\]
\[\text{Upper limit} = 5 + (2.776)(1.225) = 8.40\]
More generally, the formula for the \(95\%\) confidence interval on the mean is:
\[\text{Lower limit} = M - (t_{CL})(s_M)\]
\[\text{Upper limit} = M + (t_{CL})(s_M)\]
where \(M\) is the sample mean, \(t_{CL}\) is the \(t\) for the confidence level desired (\(0.95\) in the above example), and \(s_M\) is the estimated standard error of the mean.
We will finish with an analysis of the Stroop Data. Specifically, we will compute a confidence interval on the mean difference score. Recall that \(47\) subjects named the color of ink that words were written in. The names conflicted so that, for example, they would name the ink color of the word "blue" written in red ink. The correct response is to say "red" and ignore the fact that the word is "blue." In a second condition, subjects named the ink color of colored rectangles.
| Naming Colored Rectangle | Interference | Difference |
|---|---|---|
| 17 | 38 | 21 |
| 15 | 58 | 43 |
| 18 | 35 | 17 |
| 20 | 39 | 19 |
| 18 | 33 | 15 |
| 20 | 32 | 12 |
| 20 | 45 | 25 |
| 19 | 52 | 33 |
| 17 | 31 | 14 |
| 21 | 29 | 8 |
Table \(\PageIndex{2}\) shows the time difference between the interference and color-naming conditions for \(10\) of the \(47\) subjects. The mean time difference for all \(47\) subjects is \(16.362\) seconds and the standard deviation is \(7.470\) seconds. The standard error of the mean is \(1.090\). A \(t\) table shows the critical value of \(t\) for \(47 - 1 = 46\) degrees of freedom is \(2.013\) (for a \(95\%\) confidence interval). Therefore the confidence interval is computed as follows:
\[\text{Lower limit} = 16.362 - (2.013)(1.090) = 14.17\]
\[\text{Upper limit} = 16.362 - (2.013)(1.090) = 18.56\]
Therefore, the interference effect (difference) for the whole population is likely to be between \(14.17\) and \(18.56\) seconds.


