50: Under Construction
- Page ID
- 8644
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)It is always tempting to describe the sample with just one number “to rule them all”. Or only few numbers... This idea is behind central moments, two (or sometimes four) numbers which represent the center or central tendency of sample and its scale (variation, variability, instability, dispersion: there are many synonyms).
Third and fourth central moments are not frequently used, they represent asymmetry (shift, skewness) and sharpness (“tailedness”, kurtosis), respectively.
Median is the best
Mean is a parametric method whereas median depends less on the shape of distribution. Consequently, median is more stable, more robust. Let us go back to our seven hypothetical employees. Here are their salaries (thousands per year):
Code \(\PageIndex{1}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21)
Dramatic differences in salaries could be explained by fact that Alex is the custodian whereas Kathryn is the owner of company.
Code \(\PageIndex{2}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21) mean(salary) median(salary)
We can see that mean does not reflect typical wages very well—it is influenced by higher Kathryn’s salary. Median does a better job because it is calculated in a way radically different from mean. Median is a value that cuts off a half of ordered sample. To illustrate the point, let us make another vector, similar to our salary:
Code \(\PageIndex{3}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21) sort(salary1 <- c(salary, 22)) median(salary1)
Vector salary1 contains an even number of values, eight, so its median lies in the middle, between two central values (21 and 22).
There is also a way to make mean more robust to outliers, trimmed mean which is calculated after removal of marginal values:
Code \(\PageIndex{4}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21) mean(salary, trim=0.2)
This trimmed mean is calculated after 10% of data was taken from each end and it is significantly closer to the median.
There is another measure of central tendency aside from median and mean. It is mode, the most frequent value in the sample. It is rarely used, and mostly applied to nominal data. Here is an example (we took the variable sex from the last chapter):
Code \(\PageIndex{5}\) (Python):
sex <- c("male", "female", "male", "male", "female", "male", "male")
t.sex <- table(sex)
mode <- names(t.sex[which.max(t.sex)])
mode
Here the most common value is male\(^{[1]}\).
Often we face the task of calculating mean (or median) for the data frames. There are at least three different ways:
Code \(\PageIndex{6}\) (Python):
attach(trees) mean(Girth) mean(Height) detach(trees)
The first way uses attach() and adds columns from the table to the list of “visible” variables. Now we can address these variables using their names only, omitting the name of the data frame. If you choose to use this command, do not forget to detach() the table. Otherwise, there is a risk of loosing track of what is and is not attached. It is particularly problematic if variable names repeat across different data frames. Note that any changes made to variables will be forgotten after you detach().
The second way uses with()) which is similar to attaching, only here attachment happens within the function body:
Code \(\PageIndex{7}\) (Python):
with(trees, mean(Volume)) # Second way
The third way uses the fact that a data frame is just a list of columns. It uses grouping functions from apply() family\(^{[2]}\), for example, sapply() (“apply and simplify”):
Code \(\PageIndex{8}\) (Python):
sapply(trees, mean)
What if you must supply an argument to the function which is inside sapply()? For example, missing data will return NA without proper argument. In many cases this is possible to specify directly:
Code \(\PageIndex{9}\) (Python):
trees.n <- trees trees.n[2, 1] <- NA sapply(trees.n, mean) sapply(trees.n, mean, na.rm=TRUE)
In more complicated cases, you might want to define anonymous function (see below).
Quartiles and quantiles
Quartiles are useful in describing sample variability. Quartiles are values cutting the sample at points of 0%, 25%, 50%, 75% and 100% of the total distribution\(^{[3]}\). Median is nothing else then the third quartile (50%). The first and the fifth quartiles are minimum and maximum of the sample.
The concept of quartiles may be expanded to obtain cut-off points at any desired interval. Such measures are called quantiles (from quantum, an increment), with many special cases, e.g. percentiles for percentages. Quantiles are used also to check the normality (see later). This will calculate quartiles:
Code \(\PageIndex{10}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21) quantile(salary, c(0, 0.25, 0.5, 0.75, 1))
Another way to calculate them:
Code \(\PageIndex{11}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21) fivenum(salary)
(These two functions sometimes output slightly different results, but this is insignificant for the research. To know more, use help. Boxplots (see below) use fivenum().)
The third and most commonly used way is to run summary():
Code \(\PageIndex{12}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21) summary(salary)
summary() function is generic so it returns different results for different object types (e.g., for data frames, for measurement data and nominal data):
Code \(\PageIndex{13}\) (Python):
summary(PlantGrowth)
In addition, summary() shows the number of missing data values:
Code \(\PageIndex{14}\) (Python):
hh <- c(8, 10, NA, NA, 8, NA, 8) summary(hh)
Command summary() is also very useful at the first stage of analysis, for example, when we check the quality of data. It shows missing values and returns minimum and maximum:
Code \(\PageIndex{15}\) (Python):
err <- read.table("data/errors.txt", h=TRUE, sep=" ")
str(err)
summary(err)
We read the data file into a table and check its structure with str(). We see that variable AGE (which must be the number) has unexpectedly turned into a factor. Output of the summary() explains why: one of age measures was mistyped as a letter a. Moreover, one of the names is empty—apparently, it should have contained NA. Finally, the minimum height is 16.1 cm! This is quite impossible even for the newborns. Most likely, the decimal point was misplaced.
Variation
Most common parametric measures of variation are variance and standard deviation:
Code \(\PageIndex{16}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21) var(salary); sqrt(var(salary)); sd(salary)
(As you see, standard deviation is simply the square root of variance; in fact, this function was absent from S language.)
Useful non-parametric variation measures are IQR and MAD:
Code \(\PageIndex{17}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21) IQR(salary); mad(salary)
The first measure, inter-quartile range (IQR), the distance between the second and the fourth quartiles. Second robust measurement of the dispersion is median absolute deviation, which is based on the median of absolute differences between each value and sample median.
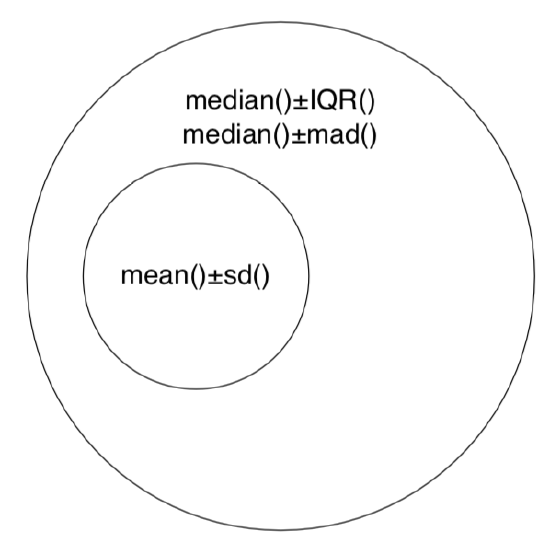
To report central value and variability together, one of frequent approaches is to use “center ± variation”. Sometimes, they do mean ± standard deviation (which mistakenly called “SEM”, ambiguous term which must be avoided), but this is not robust. Non-parametric, robust methods are always preferable, therefore “median ± IQR” or “median ± MAD” will do the best:
Code \(\PageIndex{18}\) (Python):
with(trees, paste(median(Height), IQR(Height), sep="±")) paste(median(trees$Height), mad(trees$Height), sep="±")
To report variation only, there are more ways. For example, one can use the interval where 95% of sample lays:
Code \(\PageIndex{19}\) (Python):
paste(quantile(trees$Height, c(0.025, 0.975)), collapse="-")
Note that this is not a confidence interval because quantiles and all other descriptive statistics are about sample, not about population! However, bootstrap (described in Appendix) might help to use 95% quantiles to estimate confidence interval.
... or 95% range together with a median:
Code \(\PageIndex{20}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21) paste(quantile(trees$Girth, c(0.025, 0.5, 0.975)), collapse="-")
... or scatter of “whiskers” from the boxplot:
Code \(\PageIndex{21}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21) paste(boxplot.stats(trees$Height)$stats[c(1, 5)], collapse="-")
Related with scale measures are maximum and minimum. They are easy to obtain with range() or separate min() and max() functions. Taking alone, they are not so useful because of possible outliers, but together with other measures they might be included in the report:
Code \(\PageIndex{22}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21)
HS <- fivenum(trees$Height)
paste("(", HS[1], ")", HS[2], "-", HS[4], "(", HS[5], ")", sep="")
(Here boxplot hinges were used for the main interval.)
The figure (Figure \(\PageIndex{1}\)) summarizes most important ways to report central tendency and variation with the same Euler diagram which was used to show relation between parametric and nonparametric approaches (Figure 3.1.2).
To compare the variability of characters (especially measured in different units) one may use a dimensionless coefficient of variation. It has a straightforward calculation: standard deviation divided by mean and multiplied by 100%. Here are variation coefficients for trees characteristics from a built-in dataset (trees):
Code \(\PageIndex{23}\) (Python):
salary <- c(21, 19, 27, 11, 102, 25, 21) 100*sapply(trees, sd)/colMeans(trees)
(To make things simpler, we used colMeans() which calculated means for each column. It comes from a family of similar commands with self-explanatory names: rowMeans(), colSums() and rowSums().)


