14.8: Alternatives to Pearson's Correlation
- Page ID
- 22155
The Pearson correlation coefficient is useful for a lot of things, but it does have shortcomings. One issue in particular stands out: what it actually measures is the strength of the linear relationship between two variables. In other words, what it gives you is a measure of the extent to which the data all tend to fall on a single, perfectly straight line. Often, this is a pretty good approximation to what we mean when we say “relationship”, and so the Pearson correlation is a good thing to calculation. Sometimes, it isn’t. In this section, Dr. Navarro and Dr. MO will be reviewing the correlational analysis you could use if you're a linear relationship isn't quite what you are looking for.
Spearman’s Rank Correlations
One very common situation where the Pearson correlation isn’t quite the right thing to use arises when an increase in one variable X really is reflected in an increase in another variable Y, but the nature of the relationship is more than linear (a straight line). An example of this might be the relationship between effort and reward when studying for an exam. If you put in zero effort (x-axis) into learning a subject, then you should expect a grade of 0% (y-axis). However, a little bit of effort will cause a massive improvement: just turning up to lectures means that you learn a fair bit, and if you just turn up to classes, and scribble a few things down so your grade might rise to 35%, all without a lot of effort. However, you just don’t get the same effect at the other end of the scale. As everyone knows, it takes a lot more effort to get a grade of 90% than it takes to get a grade of 55%. What this means is that, if I’ve got data looking at study effort and grades, there’s a pretty good chance that Pearson correlations will be misleading.
To illustrate, consider the data in Table \(\PageIndex{1}\), plotted in Figure \(\PageIndex{1}\), showing the relationship between hours worked and grade received for 10 students taking some class.
| Student | Hours Worked | Percentage Grade |
|---|---|---|
| A | 2 | 13 |
| B | 76 | 91 |
| C | 40 | 79 |
| D | 6 | 14 |
| E | 16 | 21 |
| F | 28 | 74 |
| G | 27 | 47 |
| H | 59 | 85 |
| I | 46 | 84 |
| J | 68 | 88 |
The curious thing about this highly fictitious data set is that increasing your effort always increases your grade. This produces a strong Pearson correlation of r=.91; the dashed line through the middle shows this linear relationship between the two variables. However, the interesting thing to note here is that there’s actually a perfect monotonic relationship between the two variables: in this example at least, increasing the hours worked always increases the grade received, as illustrated by the solid line.
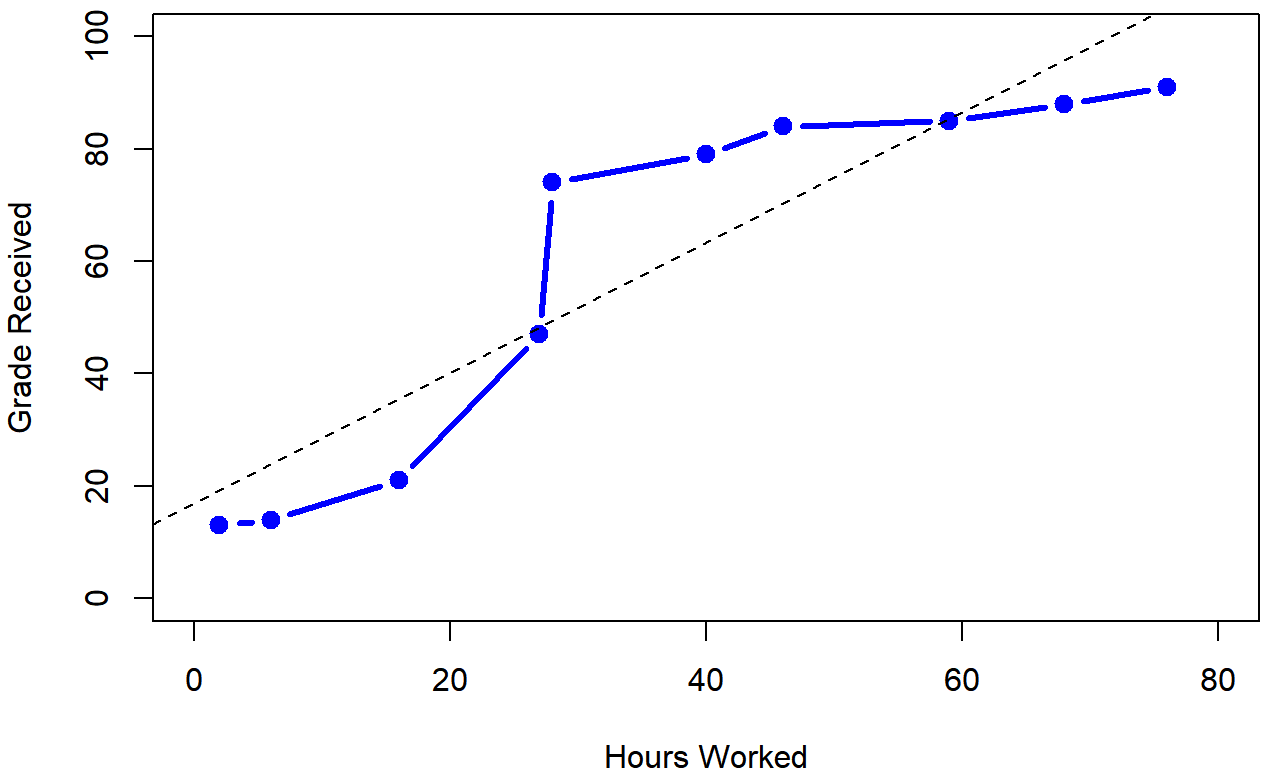
If we run a standard Pearson correlation, it shows a strong relationship between hours worked and grade received (r(8) = 0.91, p < .05), but this doesn’t actually capture the observation that increasing hours worked always increases the grade. There’s a sense here in which we want to be able to say that the correlation is perfect but for a somewhat different notion of what a “relationship” is. What we’re looking for is something that captures the fact that there is a perfect ordinal relationship here. That is, if Student A works more hours than Student B, then we can guarantee that Student A will get the better grade than Student b. That’s not what a correlation of r=.91 says at all; Pearson's r says that there's strong, positive linear relationship; as one variable goes up, the other variable goes up. It doesn't say anything about how much each variable goes up.
How should we address this? Actually, it’s really easy: if we’re looking for ordinal relationships, all we have to do is treat the data as if it were ordinal scale! So, instead of measuring effort in terms of “hours worked”, lets rank all 10 of our students in order of hours worked. That is, the student who did the least work out of anyone (2 hours) so they get the lowest rank (rank = 1). The student who was the next most distracted, putting in only 6 hours of work in over the whole semester get the next lowest rank (rank = 2). Notice that Dr. Navarro is using “rank =1” to mean “low rank”. Sometimes in everyday language we talk about “rank = 1” to mean “top rank” rather than “bottom rank”. So be careful: you can rank “from smallest value to largest value” (i.e., small equals rank 1) or you can rank “from largest value to smallest value” (i.e., large equals rank 1). In this case, I’m ranking from smallest to largest, because that’s the default way that some statistical programs run things. But in real life, it’s really easy to forget which way you set things up, so you have to put a bit of effort into remembering!
Okay, so let’s have a look at our students when we rank them from worst to best in terms of effort and reward:
| Student | Hours Worked | Rank of Hours Worked | Percentage Grade | Rank of Percentage Grade |
|---|---|---|---|---|
| A | 2 | 1 | 13 | 1 |
| D | 6 | 2 | 14 | 2 |
| E | 16 | 3 | 21 | 3 |
| G | 27 | 4 | 47 | 4 |
| F | 28 | 5 | 74 | 5 |
| C | 40 | 6 | 79 | 6 |
| I | 46 | 7 | 84 | 7 |
| H | 59 | 8 | 85 | 8 |
| J | 68 | 9 | 88 | 9 |
| B | 76 | 10 | 91 | 10 |
Hm. The rankings are identical. The student who put in the most effort got the best grade, the student with the least effort got the worst grade, etc. If we run a Pearson's correlation on the rankings, we get a perfect relationship: r(8) = 1.00, p<.05. What we’ve just re-invented is Spearman’s rank order correlation, usually denoted ρ or rho to distinguish it from the Pearson r. If we analyzed this data, we'd get a Spearman correlation of rho=1. We aren't going to get into the formulas for this one; if you have ranked or ordinal data, but you can find the formulas online or use statistical software.
For this data set, which analysis should you run? With such a small data set, it’s an open question as to which version better describes the actual relationship involved. Is it linear? Is it ordinal? We're not sure, but we can tell that increasing effort will never decrease your grade.
Phi Correlation (or Chi-Square)
As we’ve seen, Pearson's or Spearman's correlations workspretty well, and handles many of the situations that you might be interested in. One thing that many beginners find frustrating, however, is the fact that it’s not built to handle non-numeric variables. From a statistical perspective, this is perfectly sensible: Pearson and Spearman correlations are only designed to work for numeric variables
What should we do?!
As always, the answer depends on what kind of data you have. As we we’ve seen just in this chapter, if your data are purely qualitative (ratio or interval scales of measurement), then Pearson’s is perfect. If your data happens to be rankings or ordinal scale of measurement, then Spearman’s is the way to go. And if your data is purely qualitative, then Chi-Square is the way to go (which we’ll cover in depth in a few chapters).
But there’s one more cool variation of data that we haven’t talked about until now, and that’s called binary or dichotomous.
Look up “binary” or “dichotomous” to see what they mean.
The root of both words (bi- or di-) mean “two” but the Phi (sounds like “fee,” rhymes with “reality”) correlation actually uses two variables that only have two levels. You might be thinking, “That sounds like a 2x2 factorial design!” but the difference is that a 2x2 factorial design has two IVs, each with two levels, but also has a DV (the outcome variable that you measure and want to improve). The Phi correlation has one of the two variables as the DV and the DV only has two options, and one of the two variables in the IV and that IV only has two levels. Let’s see some example variables:
- Pass or Fail
- Pregnant or Not pregnant
- Urban or rural
- Yes or No
- On or Off
- Conservative or Progressive
How does this work into IVs and DVs?
- Does tutor (tutored or not-tutored) affect passing (pass or fail)?
- Does caffeine (coffee or no-coffee) affect energy (sleepy or not-sleepy)?
- Does exercise (exercise or no-exercise) affect weight loss (lose 10+ pounds or do not lose 10+ pounds)?
Again, we are not going to get into the formula for this one, but it is a unique statistical analysis that is designed for very specific variables. So when you have two binary variables, the Phi correlation is exactly what you should be using!
Curvilinear Relationships
We have one more situation in which Pearson’s correlation isn’t quite right, and that’s when we expect a non-linear relationship. We’ve seen this in scatter plots that are U-shaped or reverse-U shaped (the section of the graphing chapter on scatterplots, the section of this chapter on correlation versus causation in graphs, and the section in this chapter on strength, direction, and linearity) . In that section on correlation versus causation in graphs, we talked about how plants die if they don’t have enough water but also if they have too much water. There is not a linear relationship between water and plant growth, it is a curvilinear relationship. There are specific statistical analyses that look for specific curvilinear relationships (based on how curved it appears to be) that we aren’t going to get into here, but they are available on advanced statistical software programs.
Summary
The key thing to remember, other than that these analyses exist, is that looking at the graph is key to helping you know what kind of analysis to conduct.


