12.6: Scores on Job Application Tests
- Page ID
- 14529
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Our data come from three groups of 10 people each, all of whom applied for a single job opening: those with no college degree, those with a college degree that is not related to the job opening, and those with a college degree from a relevant field. We want to know if we can use this group membership to account for our observed variability and, by doing so, test if there is a difference between our three group means. We will start, as always, with our hypotheses.
Step 1: State the Hypotheses
Our hypotheses are concerned with the test scores of groups based on education level, so:
\[\begin{array}{c}{\mathrm{H}_{0}: \text { There is no difference between the test scores of the education groups }} \\ {\mathrm{H}_{0}: \mu_{1}=\mu_{2}=\mu_{3}}\end{array} \nonumber \]
\[\mathrm{H}_{A}: \text { At least one group of test scores is different from the rest } \nonumber \]
Again, we phrase our null hypothesis in terms of what we are actually looking for, and we use a number of population parameters equal to our number of groups.
Step 2: Find the Critical Values
Our test statistic for ANOVA, as we saw above, is \(F\). Because we are using a new test statistic, we will get a new table: the \(F\) distribution table, the top of which is shown in Figure \(\PageIndex{1}\):
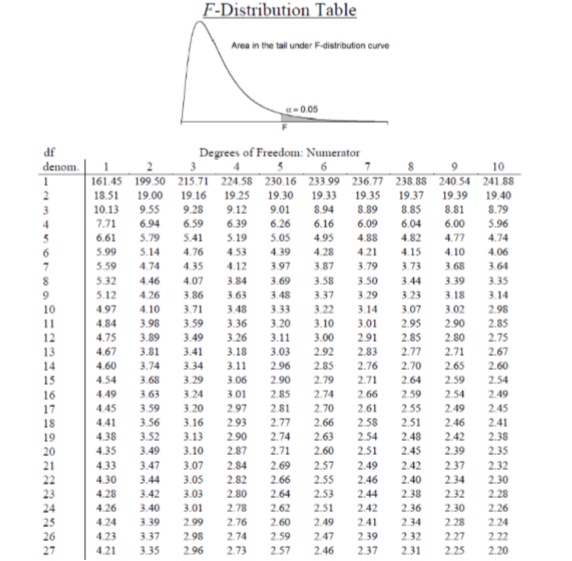
The \(F\) table only displays critical values for \(α\) = 0.05. This is because other significance levels are uncommon and so it is not worth it to use up the space to present them. There are now two degrees of freedom we must use to find our critical value: Numerator and Denominator. These correspond to the numerator and denominator of our test statistic, which, if you look at the ANOVA table presented earlier, are our Between Groups and Within Groups rows, respectively. The \(df_B\) is the “Degrees of Freedom: Numerator” because it is the degrees of freedom value used to calculate the Mean Square Between, which in turn was the numerator of our \(F\) statistic. Likewise, the \(df_W\) is the “\(df\) denom.” (short for denominator) because it is the degrees of freedom value used to calculate the Mean Square Within, which was our denominator for \(F\).
The formula for \(df_B\) is \(k – 1\), and remember that k is the number of groups we are assessing. In this example, \(k = 3\) so our \(df_B\) = 2. This tells us that we will use the second column, the one labeled 2, to find our critical value. To find the proper row, we simply calculate the \(df_W\), which was \(N – k\). The original prompt told us that we have “three groups of 10 people each,” so our total sample size is 30. This makes our value for \(df_W\) = 27. If we follow the second column down to the row for 27, we find that our critical value is 3.35. We use this critical value the same way as we did before: it is our criterion against which we will compare our obtained test statistic to determine statistical significance.
Step 3: Calculate the Test Statistic
Now that we have our hypotheses and the criterion we will use to test them, we can calculate our test statistic. To do this, we will fill in the ANOVA table. When we do so, we will work our way from left to right, filling in each cell to get our final answer. We will assume that we are given the \(SS\) values as shown below:
| Source | \(SS\) | \(df\) | \(MS\) | \(F\) |
|---|---|---|---|---|
| Between | 8246 | |||
| Within | 3020 | |||
| Total |
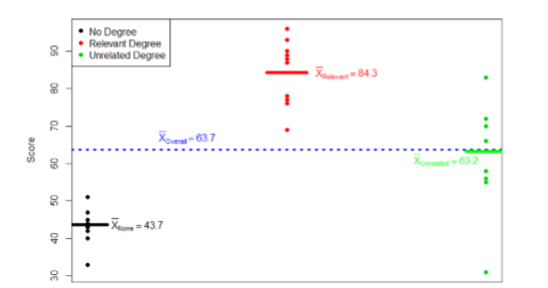
These may seem like random numbers, but remember that they are based on the distances between the groups themselves and within each group. Figure \(\PageIndex{2}\) shows the plot of the data with the group means and grand mean included. If we wanted to, we could use this information, combined with our earlier information that each group has 10 people, to calculate the Between Groups Sum of Squares by hand. However, doing so would take some time, and without the specific values of the data points, we would not be able to calculate our Within Groups Sum of Squares, so we will trust that these values are the correct ones.
We were given the sums of squares values for our first two rows, so we can use those to calculate the Total Sum of Squares.
| Source | \(SS\) | \(df\) | \(MS\) | \(F\) |
|---|---|---|---|---|
| Between | 8246 | |||
| Within | 3020 | |||
| Total | 11266 |
We also calculated our degrees of freedom earlier, so we can fill in those values. Additionally, we know that the total degrees of freedom is \(N – 1\), which is 29. This value of 29 is also the sum of the other two degrees of freedom, so everything checks out.
| Source | \(SS\) | \(df\) | \(MS\) | \(F\) |
|---|---|---|---|---|
| Between | 8246 | 2 | ||
| Within | 3020 | 27 | ||
| Total | 11266 | 29 |
Now we have everything we need to calculate our mean squares. Our \(MS\) values for each row are just the \(SS\) divided by the \(df\) for that row, giving us:
| Source | \(SS\) | \(df\) | \(MS\) | \(F\) |
|---|---|---|---|---|
| Between | 8246 | 2 | 4123 | |
| Within | 3020 | 27 | 111.85 | |
| Total | 11266 | 29 |
Remember that we do not calculate a Total Mean Square, so we leave that cell blank. Finally, we have the information we need to calculate our test statistic. \(F\) is our \(MS_B\) divided by \(MS_W\).
| Source | \(SS\) | \(df\) | \(MS\) | \(F\) |
|---|---|---|---|---|
| Between | 8246 | 2 | 4123 | 36.86 |
| Within | 3020 | 27 | 111.85 | |
| Total | 11266 | 29 |
So, working our way through the table given only two \(SS\) values and the sample size and group size given before, we calculate our test statistic to be \(F_{obt} = 36.86\), which we will compare to the critical value in step 4.
Step 4: Make the Decision
Our obtained test statistic was calculated to be \(F_{obt} = 36.86\) and our critical value was found to be \(F^* = 3.35\). Our obtained statistic is larger than our critical value, so we can reject the null hypothesis.
Reject \(H_0\). Based on our 3 groups of 10 people, we can conclude that job test scores are statistically significantly different based on education level, \(F(2,27) = 36.86, p < .05\).
Notice that when we report \(F\), we include both degrees of freedom. We always report the numerator then the denominator, separated by a comma. We must also note that, because we were only testing for any difference, we cannot yet conclude which groups are different from the others. We will do so shortly, but first, because we found a statistically significant result, we need to calculate an effect size to see how big of an effect we found.
Contributors and Attributions
Foster et al. (University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus)


