2.2: Graphing Quantitative Variables
- Page ID
- 14461
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As discussed in the section on variables in Chapter 1, quantitative variables are variables measured on a numeric scale. Height, weight, response time, subjective rating of pain, temperature, and score on an exam are all examples of quantitative variables. Quantitative variables are distinguished from categorical (sometimes called qualitative) variables such as favorite color, religion, city of birth, favorite sport in which there is no ordering or measuring involved.
There are many types of graphs that can be used to portray distributions of quantitative variables. The upcoming sections cover the following types of graphs:
- stem and leaf displays
- histograms
- frequency polygons
- box plots
- bar charts
- line graphs
- dot plots
- scatter plots (discussed in a different chapter)
Some graph types such as stem and leaf displays are best-suited for small to moderate amounts of data, whereas others such as histograms are best suited for large amounts of data. Graph types such as box plots are good at depicting differences between distributions. Scatter plots are used to show the relationship between two variables.
Stem and Leaf Displays
A stem and leaf display is a graphical method of displaying data. It is particularly useful when your data are not too numerous. In this section, we will explain how to construct and interpret this kind of graph.
As usual, we will start with an example. Consider Figure \(\PageIndex{1}\) that shows the number of touchdown passes (TD passes) thrown by each of the 31 teams in the National Football League in the 2000 season.

A stem and leaf display of the data is shown in Figure \(\PageIndex{2}\). The left portion of Figure \(\PageIndex{2}\) contains the stems. They are the numbers 3, 2, 1, and 0, arranged as a column to the left of the bars. Think of these numbers as 10’s digits. A stem of 3, for example, can be used to represent the 10’s digit in any of the numbers from 30 to 39. The numbers to the right of the bar are leaves, and they represent the 1’s digits. Every leaf in the graph therefore stands for the result of adding the leaf to 10 times its stem.

To make this clear, let us examine Figure \(\PageIndex{2}\) more closely. In the top row, the four leaves to the right of stem 3 are 2, 3, 3, and 7. Combined with the stem, these leaves represent the numbers 32, 33, 33, and 37, which are the numbers of TD passes for the first four teams in Figure \(\PageIndex{1}\). The next row has a stem of 2 and 12 leaves. Together, they represent 12 data points, namely, two occurrences of 20 TD passes, three occurrences of 21 TD passes, three occurrences of 22 TD passes, one occurrence of 23 TD passes, two occurrences of 28 TD passes, and one occurrence of 29 TD passes. We leave it to you to figure out what the third row represents. The fourth row has a stem of 0 and two leaves. It stands for the last two entries in Figure \(\PageIndex{1}\), namely 9 TD passes and 6 TD passes. (The latter two numbers may be thought of as 09 and 06.)
One purpose of a stem and leaf display is to clarify the shape of the distribution. You can see many facts about TD passes more easily in Figure \(\PageIndex{2}\) than in Figure \(\PageIndex{1}\). For example, by looking at the stems and the shape of the plot, you can tell that most of the teams had between 10 and 29 passing TD's, with a few having more and a few having less. The precise numbers of TD passes can be determined by examining the leaves.
We can make our figure even more revealing by splitting each stem into two parts. Figure \(\PageIndex{3}\) shows how to do this. The top row is reserved for numbers from 35 to 39 and holds only the 37 TD passes made by the first team in Figure \(\PageIndex{1}\). The second row is reserved for the numbers from 30 to 34 and holds the 32, 33, and 33 TD passes made by the next three teams in the table. You can see for yourself what the other rows represent.

Figure \(\PageIndex{3}\) is more revealing than Figure \(\PageIndex{2}\) because the latter figure lumps too many values into a single row. Whether you should split stems in a display depends on the exact form of your data. If rows get too long with single stems, you might try splitting them into two or more parts.
There is a variation of stem and leaf displays that is useful for comparing distributions. The two distributions are placed back to back along a common column of stems. The result is a “back-to-back stem and leaf display.” Figure \(\PageIndex{4}\) shows such a graph. It compares the numbers of TD passes in the 1998 and 2000 seasons. The stems are in the middle, the leaves to the left are for the 1998 data, and the leaves to the right are for the 2000 data. For example, the second-to-last row shows that in 1998 there were teams with 11, 12, and 13 TD passes, and in 2000 there were two teams with 12 and three teams with 14 TD passes.
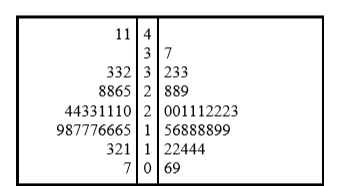
Figure \(\PageIndex{4}\) helps us see that the two seasons were similar, but that only in 1998 did any teams throw more than 40 TD passes.
There are two things about the football data that make them easy to graph with stems and leaves. First, the data are limited to whole numbers that can be represented with a one-digit stem and a one-digit leaf. Second, all the numbers are positive. If the data include numbers with three or more digits, or contain decimals, they can be rounded to two-digit accuracy. Negative values are also easily handled. Let us look at another example.
Figure \(\PageIndex{5}\) shows data from the case study Weapons and Aggression. Each value is the mean difference over a series of trials between the times it took an experimental subject to name aggressive words (like “punch”) under two conditions. In one condition, the words were preceded by a non-weapon word such as “bug.” In the second condition, the same words were preceded by a weapon word such as “gun” or “knife.” The issue addressed by the experiment was whether a preceding weapon word would speed up (or prime) pronunciation of the aggressive word compared to a non-weapon priming word. A positive difference implies greater priming of the aggressive word by the weapon word. Negative differences imply that the priming by the weapon word was less than for a neutral word.

You see that the numbers range from 43.2 to -27.4. The first value indicates that one subject was 43.2 milliseconds faster pronouncing aggressive words when they were preceded by weapon words than when preceded by neutral words. The value -27.4 indicates that another subject was 27.4 milliseconds slower pronouncing aggressive words when they were preceded by weapon words.
The data are displayed with stems and leaves in Figure \(\PageIndex{6}\). Since stem and leaf displays can only portray two whole digits (one for the stem and one for the leaf) the numbers are first rounded. Thus, the value 43.2 is rounded to 43 and represented with a stem of 4 and a leaf of 3. Similarly, 42.9 is rounded to 43. To represent negative numbers, we simply use negative stems. For example, the bottom row of the figure represents the number –27. The second-to-last row represents the numbers -10, -10, -15, etc. Once again, we have rounded the original values from Figure \(\PageIndex{5}\).

Observe that the figure contains a row headed by “0” and another headed by “-0.” The stem of 0 is for numbers between 0 and 9, whereas the stem of -0 is for numbers between 0 and -9. For example, the fifth row of the table holds the numbers 1, 2, 4, 5, 5, 8, 9 and the sixth row holds 0, -6, -7, and -9. Values that are exactly 0 before rounding should be split as evenly as possible between the “0” and “-0” rows. In Figure \(\PageIndex{5}\), none of the values are 0 before rounding. The “0” that appears in the “-0” row comes from the original value of -0.2 in the table.
Although stem and leaf displays are unwieldy for large data sets, they are often useful for data sets with up to 200 observations. Figure \(\PageIndex{7}\) portrays the distribution of populations of 185 US cities in 1998. To be included, a city had to have between 100,000 and 500,000 residents.

Since a stem and leaf plot shows only two-place accuracy, we had to round the numbers to the nearest 10,000. For example the largest number (493,559) was rounded to 490,000 and then plotted with a stem of 4 and a leaf of 9. The fourth highest number (463,201) was rounded to 460,000 and plotted with a stem of 4 and a leaf of 6. Thus, the stems represent units of 100,000 and the leaves represent units of 10,000. Notice that each stem value is split into five parts: 0-1, 2-3, 4-5, 67, and 8-9.
Whether your data can be suitably represented by a stem and leaf display depends on whether they can be rounded without loss of important information. Also, their extreme values must fit into two successive digits, as the data in Figure 11 fit into the 10,000 and 100,000 places (for leaves and stems, respectively). Deciding what kind of graph is best suited to displaying your data thus requires good judgment. Statistics is not just recipes!
Histograms
A histogram is a graphical method for displaying the shape of a distribution. It is particularly useful when there are a large number of observations. We begin with an example consisting of the scores of 642 students on a psychology test. The test consists of 197 items each graded as “correct” or “incorrect.” The students' scores ranged from 46 to 167.
The first step is to create a frequency table. Unfortunately, a simple frequency table would be too big, containing over 100 rows. To simplify the table, we group scores together as shown in Table \(\PageIndex{1}\).
| Interval's Lower Limit | Interval's Upper Limit | Class Frequency |
|---|---|---|
| 39.5 | 49.5 | 3 |
| 49.5 | 59.5 | 10 |
| 59.5 | 69.5 | 53 |
| 69.5 | 79.5 | 107 |
| 79.5 | 89.5 | 147 |
| 89.5 | 99.5 | 130 |
| 99.5 | 109.5 | 78 |
| 109.5 | 119.5 | 59 |
| 119.5 | 129.5 | 36 |
| 129.5 | 139.5 | 11 |
| 139.5 | 149.5 | 6 |
| 149.5 | 159.5 | 1 |
| 159.5 | 169.5 | 1 |
To create this table, the range of scores was broken into intervals, called class intervals. The first interval is from 39.5 to 49.5, the second from 49.5 to 59.5, etc. Next, the number of scores falling into each interval was counted to obtain the class frequencies. There are three scores in the first interval, 10 in the second, etc.
Class intervals of width 10 provide enough detail about the distribution to be revealing without making the graph too “choppy.” More information on choosing the widths of class intervals is presented later in this section. Placing the limits of the class intervals midway between two numbers (e.g., 49.5) ensures that every score will fall in an interval rather than on the boundary between intervals.
In a histogram, the class frequencies are represented by bars. The height of each bar corresponds to its class frequency. A histogram of these data is shown in Figure \(\PageIndex{8}\).
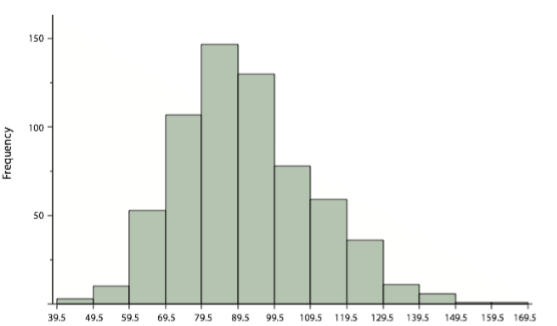
The histogram makes it plain that most of the scores are in the middle of the distribution, with fewer scores in the extremes. You can also see that the distribution is not symmetric: the scores extend to the right farther than they do to the left. The distribution is therefore said to be skewed. (We'll have more to say about shapes of distributions in Chapter 3.)
In our example, the observations are whole numbers. Histograms can also be used when the scores are measured on a more continuous scale such as the length of time (in milliseconds) required to perform a task. In this case, there is no need to worry about fence sitters since they are improbable. (It would be quite a coincidence for a task to require exactly 7 seconds, measured to the nearest thousandth of a second.) We are therefore free to choose whole numbers as boundaries for our class intervals, for example, 4000, 5000, etc. The class frequency is then the number of observations that are greater than or equal to the lower bound, and strictly less than the upper bound. For example, one interval might hold times from 4000 to 4999 milliseconds. Using whole numbers as boundaries avoids a cluttered appearance, and is the practice of many computer programs that create histograms. Note also that some computer programs label the middle of each interval rather than the end points.
Histograms can be based on relative frequencies instead of actual frequencies. Histograms based on relative frequencies show the proportion of scores in each interval rather than the number of scores. In this case, the Y-axis runs from 0 to 1 (or somewhere in between if there are no extreme proportions). You can change a histogram based on frequencies to one based on relative frequencies by (a) dividing each class frequency by the total number of observations, and then (b) plotting the quotients on the Y-axis (labeled as proportion).
There is more to be said about the widths of the class intervals, sometimes called bin widths. Your choice of bin width determines the number of class intervals. This decision, along with the choice of starting point for the first interval, affects the shape of the histogram. The best advice is to experiment with different choices of width, and to choose a histogram according to how well it communicates the shape of the distribution.
Frequency Polygons
Frequency polygons are a graphical device for understanding the shapes of distributions. They serve the same purpose as histograms, but are especially helpful for comparing sets of data. Frequency polygons are also a good choice for displaying cumulative frequency distributions.
To create a frequency polygon, start just as for histograms, by choosing a class interval. Then draw an X-axis representing the values of the scores in your data. Mark the middle of each class interval with a tick mark, and label it with the middle value represented by the class. Draw the Y-axis to indicate the frequency of each class. Place a point in the middle of each class interval at the height corresponding to its frequency. Finally, connect the points. You should include one class interval below the lowest value in your data and one above the highest value. The graph will then touch the X-axis on both sides.
A frequency polygon for 642 psychology test scores shown in Figure \(\PageIndex{8}\) was constructed from the frequency table shown in Table \(\PageIndex{2}\).
| Lower Limit | Upper Limit | Count | Cumulative Count |
|---|---|---|---|
| 29.5 | 39.5 | 0 | 0 |
| 39.5 | 49.5 | 3 | 3 |
| 49.5 | 59.5 | 10 | 13 |
| 59.5 | 69.5 | 53 | 66 |
| 69.5 | 79.5 | 107 | 173 |
| 79.5 | 89.5 | 147 | 320 |
| 89.5 | 99.5 | 130 | 450 |
| 99.5 | 109.5 | 78 | 528 |
| 109.5 | 119.5 | 59 | 587 |
| 119.5 | 129.5 | 36 | 623 |
| 129.5 | 139.5 | 11 | 634 |
| 139.5 | 149.5 | 6 | 640 |
| 149.5 | 159.5 | 1 | 641 |
| 159.5 | 169.5 | 1 | 642 |
| 169.5 | 170.5 | 0 | 642 |
The first label on the X-axis is 35. This represents an interval extending from 29.5 to 39.5. Since the lowest test score is 46, this interval has a frequency of 0. The point labeled 45 represents the interval from 39.5 to 49.5. There are three scores in this interval. There are 147 scores in the interval that surrounds 85.
You can easily discern the shape of the distribution from Figure \(\PageIndex{9}\). Most of the scores are between 65 and 115. It is clear that the distribution is not symmetric inasmuch as good scores (to the right) trail off more gradually than poor scores (to the left). In the terminology of Chapter 3 (where we will study shapes of distributions more systematically), the distribution is skewed.
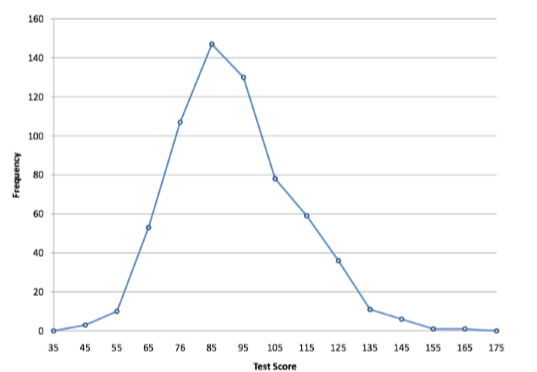
Figure \(\PageIndex{9}\): Frequency polygon for the psychology test scores.
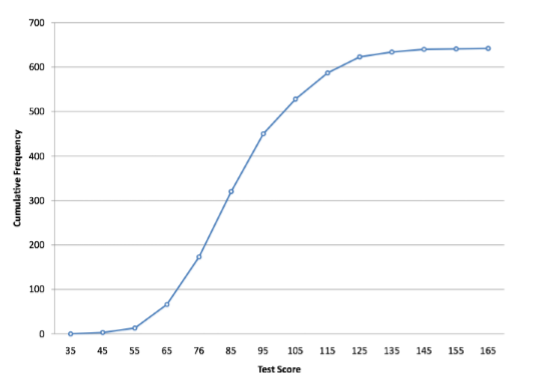
A cumulative frequency polygon for the same test scores is shown in Figure \(\PageIndex{10}\). The graph is the same as before except that the Y value for each point is the number of students in the corresponding class interval plus all numbers in lower intervals. For example, there are no scores in the interval labeled “35,” three in the interval “45,” and 10 in the interval “55.” Therefore, the Y value corresponding to “55” is 13. Since 642 students took the test, the cumulative frequency for the last interval is 642.
Frequency polygons are useful for comparing distributions. This is achieved by overlaying the frequency polygons drawn for different data sets. Figure 2.1.3 provides an example. The data come from a task in which the goal is to move a computer cursor to a target on the screen as fast as possible. On 20 of the trials, the target was a small rectangle; on the other 20, the target was a large rectangle. Time to reach the target was recorded on each trial. The two distributions (one for each target) are plotted together in Figure \(\PageIndex{11}\). The figure shows that, although there is some overlap in times, it generally took longer to move the cursor to the small target than to the large one.
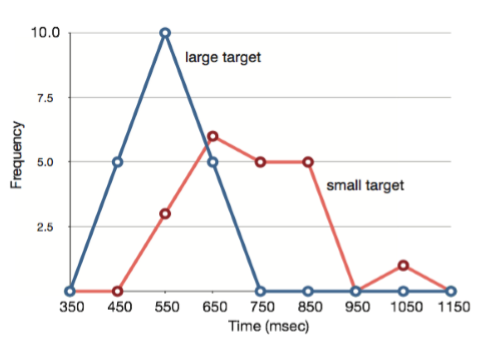
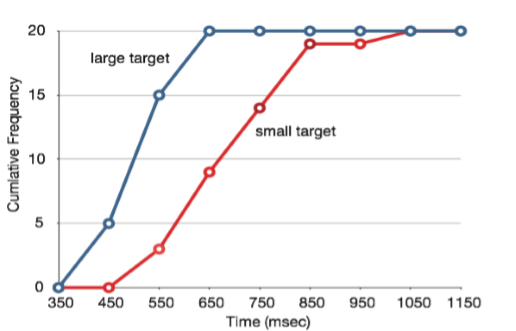
It is also possible to plot two cumulative frequency distributions in the same graph. This is illustrated in Figure \(\PageIndex{12}\) using the same data from the cursor task. The difference in distributions for the two targets is again evident.
Box Plots
We have already discussed techniques for visually representing data (see histograms and frequency polygons). In this section we present another important graph, called a box plot. Box plots are useful for identifying outliers and for comparing distributions. We will explain box plots with the help of data from an in-class experiment. Students in Introductory Statistics were presented with a page containing 30 colored rectangles. Their task was to name the colors as quickly as possible. Their times (in seconds) were recorded. We'll compare the scores for the 16 men and 31 women who participated in the experiment by making separate box plots for each gender. Such a display is said to involve parallel box plots.
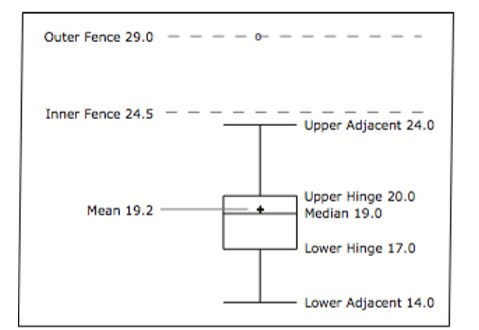
There are several steps in constructing a box plot. The first relies on the 25th, 50th, and 75th percentiles in the distribution of scores. Figure \(\PageIndex{14}\) shows how these three statistics are used. For each gender we draw a box extending from the 25th percentile to the 75th percentile. The 50th percentile is drawn inside the box. Therefore, the bottom of each box is the 25th percentile, the top is the 75th percentile, and the line in the middle is the 50th percentile. The data for the women in our sample are shown in Figure \(\PageIndex{13}\).

For these data, the 25th percentile is 17, the 50th percentile is 19, and the 75th percentile is 20. For the men (whose data are not shown), the 25th percentile is 19, the 50th percentile is 22.5, and the 75th percentile is 25.5.
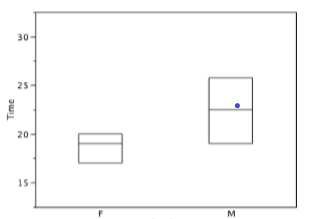
Before proceeding, the terminology in Table \(\PageIndex{3}\) is helpful.
| Name | Formula | Value |
|---|---|---|
| Upper Hinge | 75th Percentile | 20 |
| Lower Hinge | 25th Percentile | 17 |
| H-Spread | Upper Hinge - Lower Hinge | 3 |
| Step | 1.5 x H-Spread | 4.5 |
| Upper Inner Fence | Upper Hinge + 1 Step | 24.5 |
| Lower Inner Fence | Lower Hinge - 1 Step | 12.5 |
| Upper Outer Fence | Upper Hinge + 2 Steps | 29 |
| Lower Outer Fence | Lower Hinge - 2 Steps | 8 |
| Upper Adjacent | Largest value below Upper Inner Fence | 24 |
| Lower Adjacent | Smallest value above Lower Inner Fence | 14 |
| Outside Value | A value beyond an Inner Fence but not beyond an Outer Fence | 29 |
| Far Out Value | A value beyond an Outer Fence | None |
Continuing with the box plots, we put “whiskers” above and below each box to give additional information about the spread of data. Whiskers are vertical lines that end in a horizontal stroke. Whiskers are drawn from the upper and lower hinges to the upper and lower adjacent values (24 and 14 for the women's data), as shown in Figure \(\PageIndex{15}\).
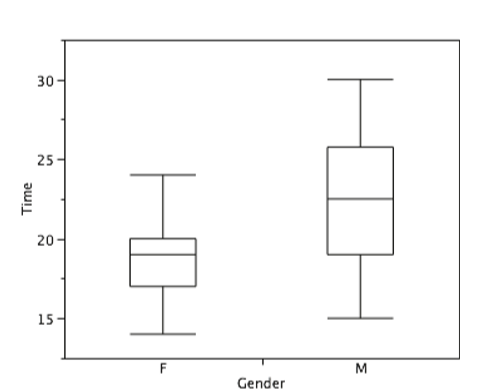
Figure \(\PageIndex{15}\): The box plots with the whiskers drawn.
Although we don't draw whiskers all the way to outside or far out values, we still wish to represent them in our box plots. This is achieved by adding additional marks beyond the whiskers. Specifically, outside values are indicated by small “o's” and far out values are indicated by asterisks (*). In our data, there are no farout values and just one outside value. This outside value of 29 is for the women and is shown in Figure \(\PageIndex{16}\).
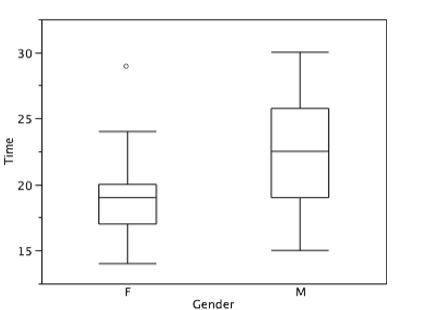
There is one more mark to include in box plots (although sometimes it is omitted). We indicate the mean score for a group by inserting a plus sign. Figure \(\PageIndex{17}\) shows the result of adding means to our box plots.
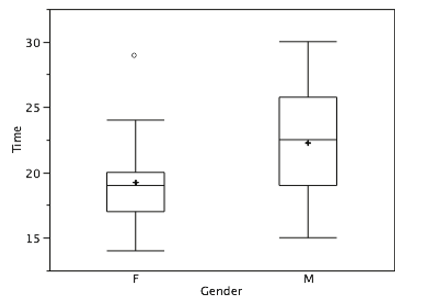
Figure \(\PageIndex{17}\) provides a revealing summary of the data. Since half the scores in a distribution are between the hinges (recall that the hinges are the 25th and 75th percentiles), we see that half the women's times are between 17 and 20 seconds whereas half the men's times are between 19 and 25.5 seconds. We also see that women generally named the colors faster than the men did, although one woman was slower than almost all of the men. Figure \(\PageIndex{18}\) shows the box plot for the women's data with detailed labels.
Box plots provide basic information about a distribution. For example, a distribution with a positive skew would have a longer whisker in the positive direction than in the negative direction. A larger mean than median would also indicate a positive skew. Box plots are good at portraying extreme values and are especially good at showing differences between distributions. However, many of the details of a distribution are not revealed in a box plot and to examine these details one should use create a histogram and/or a stem and leaf display.
Bar Charts
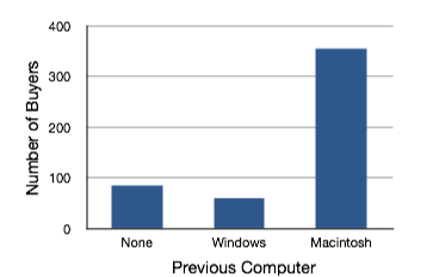
In the section on qualitative variables, we saw how bar charts could be used to illustrate the frequencies of different categories. For example, the bar chart shown in Figure \(\PageIndex{19}\) shows how many purchasers of iMac computers were previous Macintosh users, previous Windows users, and new computer purchasers.
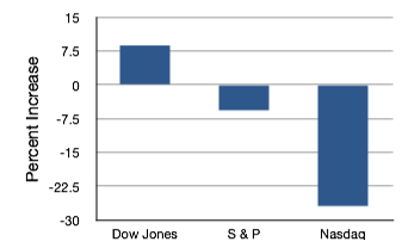
In this section we show how bar charts can be used to present other kinds of quantitative information, not just frequency counts. The bar chart in Figure \(\PageIndex{20}\) shows the percent increases in the Dow Jones, Standard and Poor 500 (S & P), and Nasdaq stock indexes from May 24th 2000 to May 24th 2001. Notice that both the S & P and the Nasdaq had “negative increases” which means that they decreased in value. In this bar chart, the Y-axis is not frequency but rather the signed quantity percentage increase.
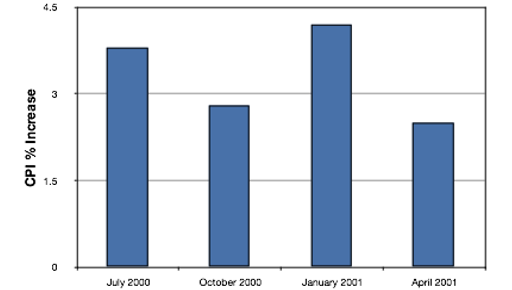
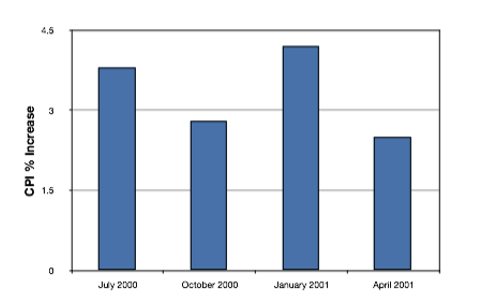
Bar charts are particularly effective for showing change over time. Figure \(\PageIndex{21}\), for example, shows the percent increase in the Consumer Price Index (CPI) over four three-month periods. The fluctuation in inflation is apparent in the graph.
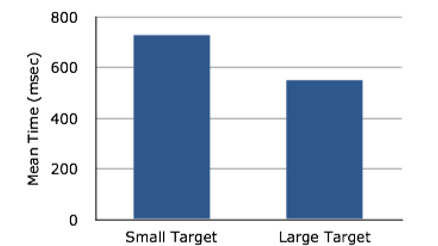
Bar charts are often used to compare the means of different experimental conditions. Figure 2.1.4 shows the mean time it took one of us (DL) to move the cursor to either a small target or a large target. On average, more time was required for small targets than for large ones.
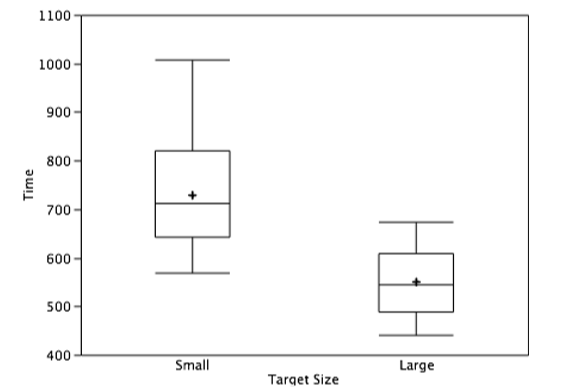
Although bar charts can display means, we do not recommend them for this purpose. Box plots should be used instead since they provide more information than bar charts without taking up more space. For example, a box plot of the cursor-movement data is shown in Figure \(\PageIndex{23}\). You can see that Figure \(\PageIndex{23}\) reveals more about the distribution of movement times than does Figure \(\PageIndex{22}\).
The section on qualitative variables presented earlier in this chapter discussed the use of bar charts for comparing distributions. Some common graphical mistakes were also noted. The earlier discussion applies equally well to the use of bar charts to display quantitative variables.
Line Graphs
A line graph is a bar graph with the tops of the bars represented by points joined by lines (the rest of the bar is suppressed). For example, Figure \(\PageIndex{24}\) was presented in the section on bar charts and shows changes in the Consumer Price Index (CPI) over time.
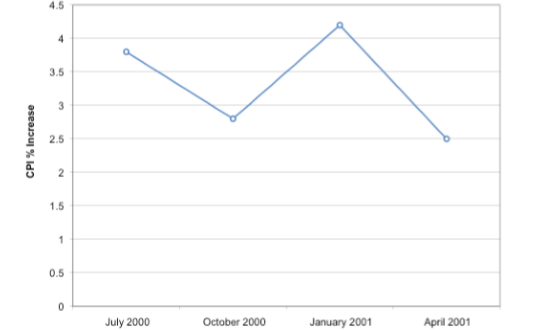
A line graph of these same data is shown in Figure \(\PageIndex{25}\). Although the figures are similar, the line graph emphasizes the change from period to period.
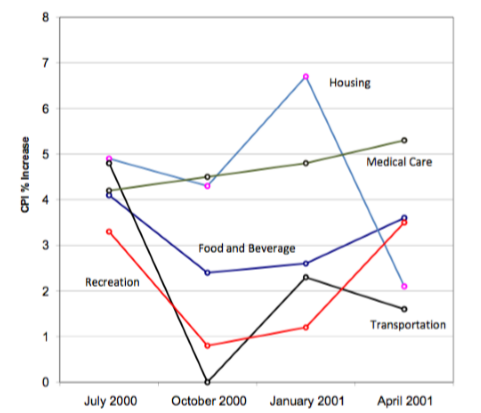
Line graphs are appropriate only when both the X- and Y-axes display ordered (rather than qualitative) variables. Although bar charts can also be used in this situation, line graphs are generally better at comparing changes over time. Figure \(\PageIndex{26}\), for example, shows percent increases and decreases in five components of the CPI. The figure makes it easy to see that medical costs had a steadier progression than the other components. Although you could create an analogous bar chart, its interpretation would not be as easy.
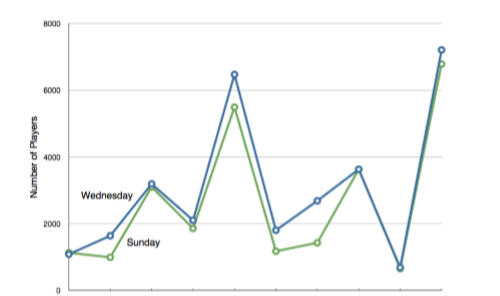
Let us stress that it is misleading to use a line graph when the X-axis contains merely qualitative variables. Figure \(\PageIndex{27}\) inappropriately shows a line graph of the card game data from Yahoo, discussed in the section on qualitative variables. The defect in Figure \(\PageIndex{27}\) is that it gives the false impression that the games are naturally ordered in a numerical way.
The Shape of Distribution
Finally, it is useful to present discussion on how we describe the shapes of distributions, which we will revisit in the next chapter to learn how different shapes affect our numerical descriptors of data and distributions.
The primary characteristic we are concerned about when assessing the shape of a distribution is whether the distribution is symmetrical or skewed. A symmetrical distribution, as the name suggests, can be cut down the center to form 2 mirror images. Although in practice we will never get a perfectly symmetrical distribution, we would like our data to be as close to symmetrical as possible for reasons we delve into in Chapter 3. Many types of distributions are symmetrical, but by far the most common and pertinent distribution at this point is the normal distribution, shown in Figure \(\PageIndex{28}\). Notice that although the symmetry is not perfect (for instance, the bar just to the right of the center is taller than the one just to the left), the two sides are roughly the same shape. The normal distribution has a single peak, known as the center, and two tails that extend out equally, forming what is known as a bell shape or bell curve.
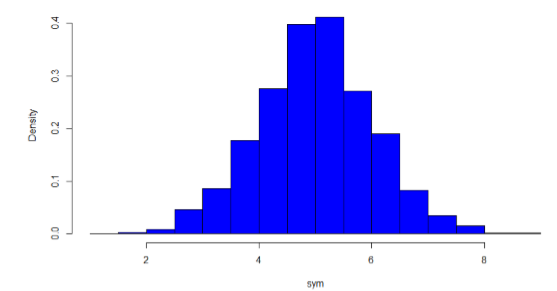
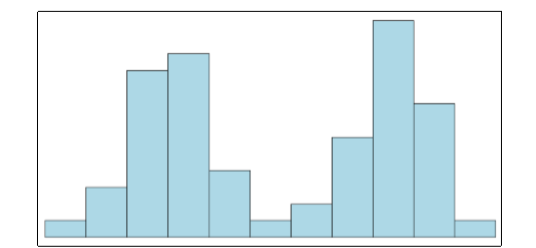
Symmetrical distributions can also have multiple peaks. Figure \(\PageIndex{29}\) shows a bimodal distribution, named for the two peaks that lie roughly symmetrically on either side of the center point. As we will see in the next chapter, this is not a particularly desirable characteristic of our data, and, worse, this is a relatively difficult characteristic to detect numerically. Thus, it is important to visualize your data before moving ahead with any formal analyses.
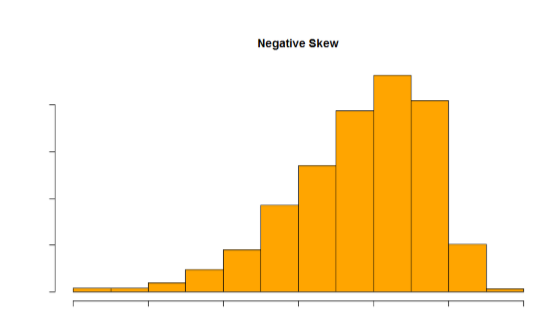
Distributions that are not symmetrical also come in many forms, more than can be described here. The most common asymmetry to be encountered is referred to as skew, in which one of the two tails of the distribution is disproportionately longer than the other. This property can affect the value of the averages we use in our analyses and make them an inaccurate representation of our data, which causes many problems.
Skew can either be positive or negative (also known as right or left, respectively), based on which tail is longer. It is very easy to get the two confused at first; many students want to describe the skew by where the bulk of the data (larger portion of the histogram, known as the body) is placed, but the correct determination is based on which tail is longer. You can think of the tail as an arrow: whichever direction the arrow is pointing is the direction of the skew. Figures \(\PageIndex{30}\) and \(\PageIndex{31}\) show positive (right) and negative (left) skew, respectively.
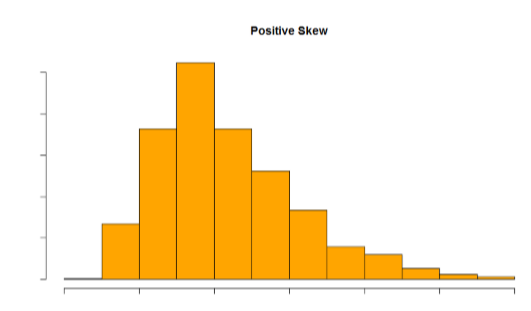
Figure \(\PageIndex{30}\): A positively skewed distribution.
Contributors and Attributions
Foster et al. (University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus)


