Learning Outcomes
- Read a Venn Diagram to extract information.
- Draw a Venn Diagram.
Venn Diagrams are a simple way of visualizing how sets interact. Many times we will see a long wordy sentence that describes a numerical situation, but it is a challenge to understand. As the saying goes, "A picture is worth a thousand words." In particular, a Venn Diagram describes how many elements are in each set displayed and how many elements are in their intersections and complements.
Example \(\PageIndex{1}\)
Consider the Venn Diagram shown below.
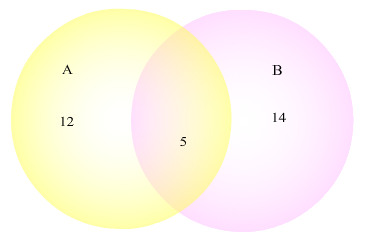
Describe how many elements are in each of the sets.
Solution
Once we understand how to read the Venn Diagram we can use it in many applications. For the Venn Diagram above, there are 12 from A that are not in B, there are 5 in both A and B, and there are 14 in B that are not in A. If we wanted to find the total in A, we would just add 12 and 5 to get 17 total in A. Similarly, there are 19 total in B.
Example \(\PageIndex{2}\)
Consider the Venn Diagram below that shows the results of a study asking students whether their first college class was at the same place they are at now, whether they are right handed, and whether they are enjoying their experience at their college.
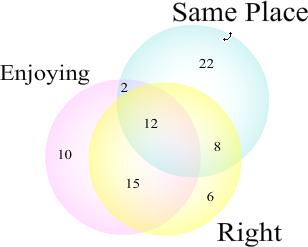
Determine how many students are:
- Right handed and enjoy college.
- At the same place but not right handed.
- Enjoy college.
Solution
- To be right handed and enjoy college they must be in both the Right circle and the Enjoying circle. Notice that the numbers 12 and 15 are in both these circles. Thus, there are 12 + 15 = 27 total students who are right handed and enjoy college.
- To be in the same place and not be right handed, the number must be in the same place circle but not in the right circle. We see that 2 and 22 are the numbers in the same place circle but not in the right circle. Adding these gives 2 + 22 = 24 total students who are at the same place but not right handed.
- We must count all the numbers in the Enjoying circle. These are 2, 10, 12, and 15. Adding these up gives: 2 + 10 + 12 + 15 = 39. Thus, 39 students enjoy college.
Example \(\PageIndex{3}\)
Suppose that a group of 40 households was looked at. 24 of them housed dogs, 30 of them housed cats, and 18 of them housed both cats and dogs. Sketch a Venn Diagram that displays this information.
Solution
To get ready to sketch the Venn Diagram, we first plan on what it will look like. There are two main groups here: houses with dogs and houses with cats. Therefore we will have two circles. The intersection will have the number 18. Since there are 24 houses with dogs and 18 also have cats, we subtract 24 - 18 = 6 to find the houses with dogs but no cats. Similarly, we subtract 30 - 18 = 12 houses with cats and no dogs. If we add 18 + 6 + 12 = 36, we find the total number of houses with a dog, cat or both. Therefore there are 40 - 36 = 4 houses without any pets. Now we are ready to put in the numbers into the Venn Diagram. It is shown below.
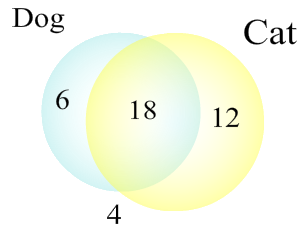
Exercise
Suppose that a group of 55 businesses was researched. 29 of them were open on the weekends, 25 of them paid more than minimum wage for everyone , 17 of them were both open on the weekends and paid more than minimum wage for everyone, and 4 of them were government consulting businesses. None of the government consulting businesses were open on the weekend nor did they pay more than minimum wage for everyone. Sketch a Venn Diagram that displays this information.





