1.3: Data Collection and Sampling Techniques
- Last updated
- Save as PDF
- Page ID
- 10909
The first step in conducting research is to identify topics or questions that are to be investigated. A clearly laid out research question is helpful in identifying what subjects or cases should be studied and what variables are important. It is also important to consider how data are collected so that they are reliable and help achieve the research goals.
Populations and samples
Consider the following three research questions:
- What is the average mercury content in sword sh in the Atlantic Ocean?
- Over the last 5 years, what is the average time to degree for Duke undergraduate students?
- Does a new drug reduce the number of deaths in patients with severe heart disease?
Each research question refers to a target population. In the rst question, the target population is all sword sh in the Atlantic ocean, and each sh represents a case. Often times, it is too expensive to collect data for every case in a population. Instead, a sample is taken. A sample represents a subset of the cases and is often a small fraction of the population. For instance, 60 sword sh (or some other number) in the population might be selected, and this sample data may be used to provide an estimate of the population average and answer the research question.
Exercise
Exercise 1.7 For the second and third questions above, identify the target population and what represents an individual case.10
Anecdotal Evidence
Consider the following possible responses to the three research questions:
- A man on the news got mercury poisoning from eating sword sh, so the average mercury concentration in sword sh must be dangerously high.
- I met two students who took more than 7 years to graduate from Duke, so it must take longer to graduate at Duke than at many other colleges.
- My friend's dad had a heart attack and died after they gave him a new heart disease drug, so the drug must not work.
Each of the conclusions are based on some data. However, there are two problems. First, the data only represent one or two cases. Second, and more importantly, it is unclear whether these cases are actually representative of the population. Data collected in this haphazard fashion are called anecdotal evidence.
10(2) Notice that the rst question is only relevant to students who complete their degree; the average cannot be computed using a student who never nished her degree. Thus, only Duke undergraduate students who have graduated in the last ve years represent cases in the population under consideration. Each such student would represent an individual case. (3) A person with severe heart disease represents a case. The population includes all people with severe heart disease.

Anecdotal evidence
Be careful of data collected in a haphazard fashion. Such evidence may be true and veri able, but it may only represent extraordinary cases.
Anecdotal evidence typically is composed of unusual cases that we recall based on their striking characteristics. For instance, we are more likely to remember the two people we met who took 7 years to graduate than the six others who graduated in four years. Instead of looking at the most unusual cases, we should examine a sample of many cases that represent the population.
Sampling from a Population
We might try to estimate the time to graduation for Duke undergraduates in the last 5 years by collecting a sample of students. All graduates in the last 5 years represent the population, and graduates who are selected for review are collectively called the sample. In general, we always seek to randomly select a sample from a population. The most basic type of random selection is equivalent to how raffles are conducted. For example, in selecting graduates, we could write each graduate's name on a raffle ticket and draw 100 tickets. The selected names would represent a random sample of 100 graduates. Why pick a sample randomly? Why not just pick a sample by hand? Consider the following scenario.
Example
Example 1.8 Suppose we ask a student who happens to be majoring in nutrition to select several graduates for the study. What kind of students do you think she might collect? Do you think her sample would be representative of all graduates?
Perhaps she would pick a disproportionate number of graduates from health-related fields. Or perhaps her selection would be well-representative of the population. When selecting samples by hand, we run the risk of picking a biased sample, even if that bias is unintentional or difficult to discern.
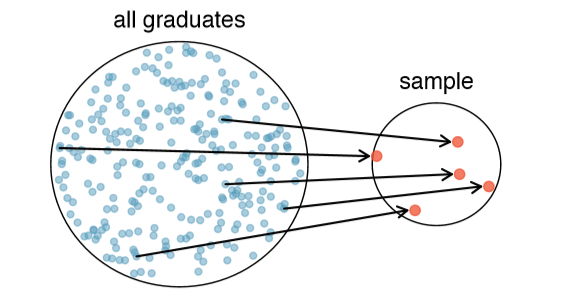
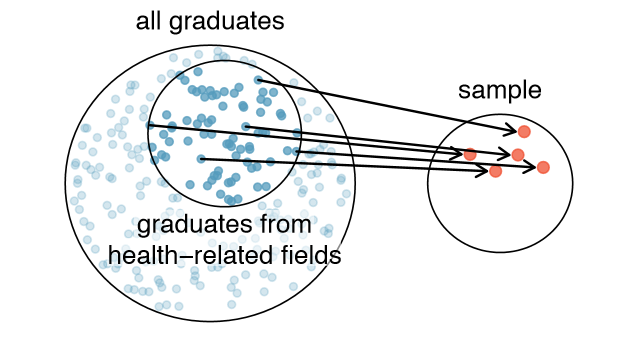
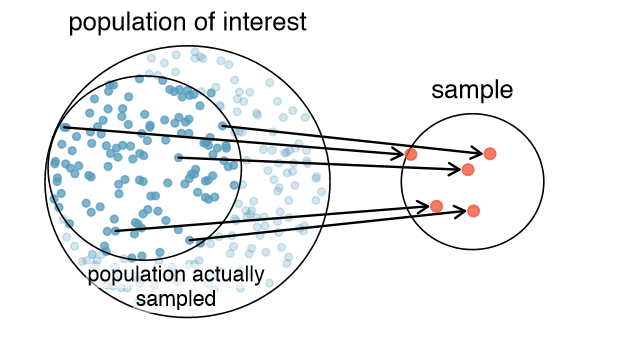
If someone was permitted to pick and choose exactly which graduates were included in the sample, it is entirely possible that the sample could be skewed to that person's interests, which may be entirely unintentional. This introduces bias into a sample. Sampling randomly helps resolve this problem. The most basic random sample is called a simple random sample, and it is the equivalent of using a raffle to select cases. This means that each case in the population has an equal chance of being included and there is no implied connection between the cases in the sample.
The act of taking a simple random sample helps minimize bias, however, bias can crop up in other ways. Even when people are picked at random, e.g. for surveys, caution must be exercised if the non-response is high. For instance, if only 30% of the people randomly sampled for a survey actually respond, then it is unclear whether the results are representative of the entire population. This non-response bias can skew results.
Another common downfall is a convenience sample, where individuals who are easily accessible are more likely to be included in the sample. For instance, if a political survey is done by stopping people walking in the Bronx, this will not represent all of New York City. It is often diffcult to discern what sub-population a convenience sample represents.
Exercise
Exercise 1.9 We can easily access ratings for products, sellers, and companies through websites. These ratings are based only on those people who go out of their way to provide a rating. If 50% of online reviews for a product are negative, do you think this means that 50% of buyers are dissatisfied with the product?11
11Answers will vary. From our own anecdotal experiences, we believe people tend to rant more about products that fell below expectations than rave about those that perform as expected. For this reason, we suspect there is a negative bias in product ratings on sites like Amazon. However, since our experiences may not be representative, we also keep an open mind should data on the subject become available.
Explanatory and Response Variables
Consider the following question from page 7 for the county data set:
(1) Is federal spending, on average, higher or lower in counties with high rates of poverty?
If we suspect poverty might a ect spending in a county, then poverty is the explanatory variable and federal spending is the response variable in the relationship.12 If there are many variables, it may be possible to consider a number of them as explanatory variables.
|
TIP: Explanatory and response variables To identify the explanatory variable in a pair of variables, identify which of the two is suspected of a ecting the other and plan an appropriate analysis. \[\text{explanatory variable}\xrightarrow { \text {might affect}} \text {response variable}\] |
|
Caution: association does not imply causation Labeling variables as explanatory and response does not guarantee the relationship between the two is actually causal, even if there is an association identi ed between the two variables. We use these labels only to keep track of which variable we suspect a ects the other. |
In some cases, there is no explanatory or response variable. Consider the following question from page 7:
(2) If homeownership is lower than the national average in one county, will the percent of multi-unit structures in that county likely be above or below the national average?
It is difficult to decide which of these variables should be considered the explanatory and response variable, i.e. the direction is ambiguous, so no explanatory or response labels are suggested here.
12Sometimes the explanatory variable is called the independent variable and the response variable is called the dependent variable. However, this becomes confusing since a pair of variables might be independent or dependent, so we avoid this language.
Introducing observational studies and experiments
There are two primary types of data collection: observational studies and experiments.
Researchers perform an observational study when they collect data in a way that does not directly interfere with how the data arise. For instance, researchers may collect information via surveys, review medical or company records, or follow a cohort of many similar individuals to study why certain diseases might develop. In each of these situations, researchers merely observe the data that arise. In general, observational studies can provide evidence of a naturally occurring association between variables, but they cannot by themselves show a causal connection.
When researchers want to investigate the possibility of a causal connection, they conduct an experiment. Usually there will be both an explanatory and a response variable. For instance, we may suspect administering a drug will reduce mortality in heart attack patients over the following year. To check if there really is a causal connection between the explanatory variable and the response, researchers will collect a sample of individuals and split them into groups. The individuals in each group are assigned a treatment. When individuals are randomly assigned to a group, the experiment is called a randomized experiment. For example, each heart attack patient in the drug trial could be randomly assigned, perhaps by flipping a coin, into one of two groups: the first group receives a placebo (fake treatment) and the second group receives the drug. See the case study in Section 1.1 for another example of an experiment, though that study did not employ a placebo.
TIP: association \(\ne\) causation
In general, association does not imply causation, and causation can only be inferred from a randomized experiment.


