4.2E: Exercises for Section 4.1
- Page ID
- 25957
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In exercises 1 - 3, find the quantities for the given equation.
1) Find \(\frac{dy}{dt}\) at \(x=1\) and \(y=x^2+3\) if \(\frac{dx}{dt}=4.\)
- Answer
- \(\dfrac{dy}{dt} = 8\)
2) Find \(\frac{dx}{dt}\) at \(x=−2\) and \(y=2x^2+1\) if \(\frac{dy}{dt}=−1.\)
3) Find \(\frac{dz}{dt}\) at \((x,y)=(1,3)\) and \(z^2=x^2+y^2\) if \(\frac{dx}{dt}=4\) and \(\frac{dy}{dt}=3\).
- Answer
- \(\dfrac{dz}{dt} = \frac{13}{\sqrt{10}}\)
In exercises 4 - 15, sketch the situation if necessary and used related rates to solve for the quantities.
4) [T] If two electrical resistors are connected in parallel, the total resistance (measured in ohms, denoted by the Greek capital letter omega, \(Ω\)) is given by the equation \(\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}.\) If \(R_1\) is increasing at a rate of \(0.5Ω/\text{min}\) and \(R_2\) decreases at a rate of \(1.1Ω/\text{min}\), at what rate does the total resistance change when \(R_1=20Ω\) and \(R_2=50Ω/\text{min}\)?
5) A \(10\)-ft ladder is leaning against a wall. If the top of the ladder slides down the wall at a rate of \(2\) ft/sec, how fast is the bottom moving along the ground when the bottom of the ladder is \(5\) ft from the wall?
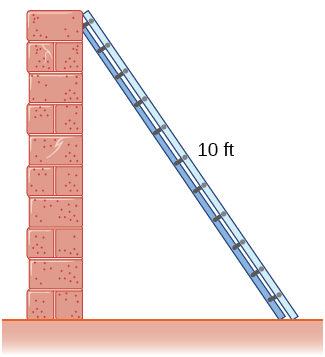
- Answer
- \(2\sqrt{3}\) ft/sec
6) A \(25\)-ft ladder is leaning against a wall. If we push the ladder toward the wall at a rate of \(1\) ft/sec, and the bottom of the ladder is initially \(20\) ft away from the wall, how fast does the ladder move up the wall \(5\) sec after we start pushing?
7) Two airplanes are flying in the air at the same height: airplane A is flying east at \(250\) mi/h and airplane B is flying north at \(300\) mi/h. If they are both heading to the same airport, located \(30\) miles east of airplane A and \(40\) miles north of airplane B, at what rate is the distance between the airplanes changing?
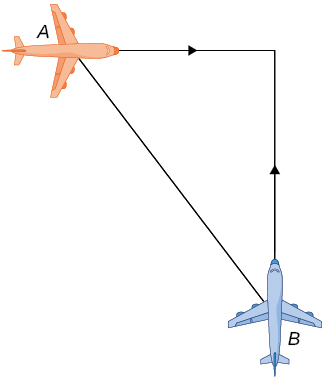
- Answer
- The distance is decreasing at \(390\) mi/h.
8) You and a friend are riding your bikes to a restaurant that you think is east; your friend thinks the restaurant is north. You both leave from the same point, with you riding at \(16\) mph east and your friend riding \(12\) mph north. After you traveled \(4\) mi, at what rate is the distance between you changing?
9) Two buses are driving along parallel freeways that are \(5\) mi apart, one heading east and the other heading west. Assuming that each bus drives a constant \(55\) mph, find the rate at which the distance between the buses is changing when they are \(13\) mi apart (as the crow flies), heading toward each other.
- Answer
- The distance between them shrinks at a rate of \(\frac{1320}{13}≈101.5\) mph.
10) A \(6\)-ft-tall person walks away from a \(10\)-ft lamppost at a constant rate of \(3\) ft/sec. What is the rate that the tip of the shadow moves away from the pole when the person is \(10\) ft away from the pole?
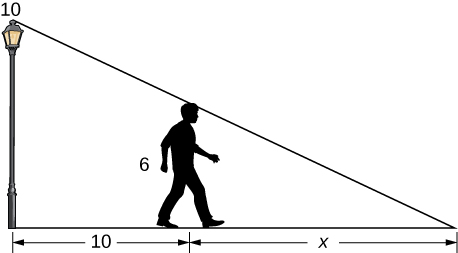
11) Using the previous problem, what is the rate at which the tip of the shadow moves away from the person when the person is \(10\) ft from the pole?
- Answer
- \(\frac{9}{2}\) ft/sec
12) A \(5\)-ft-tall person walks toward a wall at a rate of \(2\) ft/sec. A spotlight is located on the ground \(40\) ft from the wall. How fast does the height of the person’s shadow on the wall change when the person is \(10\) ft from the wall?
13) Using the previous problem, what is the rate at which the shadow changes when the person is \(10\) ft from the wall, if the person is walking away from the wall at a rate of \(2\) ft/sec?
- Answer
- It grows at a rate \(\frac{4}{9}\) ft/sec
14) A helicopter starting on the ground is rising directly into the air at a rate of \(25\) ft/sec. You are running on the ground starting directly under the helicopter at a rate of \(10\) ft/sec. Find the rate of change of the distance between the helicopter and yourself after \(5\) sec.
15) Using the previous problem, assuming the helicopter is again rising at a rate of \(25\) ft/sec and you are running on the ground starting directly under the helicopter at a rate of \(10\) ft/sec, what is the rate at which the distance between you and the helicopter is changing when the helicopter has risen to a height of \(60\) ft in the air, assuming that, initially, it was \(30\) ft above you?
- Answer
- The distance is increasing at \(\frac{135\sqrt{26}}{26}\) ft/sec
In exercises 16 - 24, draw and label diagrams to help solve the related-rates problems.
16) The side of a cube increases at a rate of \(\frac{1}{2}\) m/sec. Find the rate at which the volume of the cube increases when the side of the cube is \(4\) m.
17) The volume of a cube decreases at a rate of \(10 \text{ m}^3\)/sec. Find the rate at which the side of the cube changes when the side of the cube is \(2\) m.
- Answer
- \(−\frac{5}{6}\) m/sec
18) The radius of a circle increases at a rate of \(2\) m/sec. Find the rate at which the area of the circle increases when the radius is \(5\) m.
19) The radius of a sphere decreases at a rate of \(3\) m/sec. Find the rate at which the surface area decreases when the radius is \(10\) m.
- Answer
- \(240π \,\text{m}^2\text{/sec}\)
20) The radius of a sphere increases at a rate of \(1\) m/sec. Find the rate at which the volume increases when the radius is \(20\) m.
21) The radius of a sphere is increasing at a rate of \(9\) cm/sec. Find the radius of the sphere when the volume and the radius of the sphere are increasing at the same numerical rate.
- Answer
- \(\frac{1}{2\sqrt{π}}\) cm
22) The base of a triangle is shrinking at a rate of \(1\) cm/min and the height of the triangle is increasing at a rate of \(5\) cm/min. Find the rate at which the area of the triangle changes when the height is \(22\) cm and the base is \(10\) cm.
23) A triangle has two constant sides of length \(3\) ft and \(5\) ft. The angle between these two sides is increasing at a rate of \(0.1\) rad/sec. Find the rate at which the area of the triangle is changing when the angle between the two sides is \(π/6.\)
- Answer
- The area is increasing at a rate \(\frac{3\sqrt{3}}{8}\,\text{ft}^2\text{/sec}\).
24) A triangle has a height that is increasing at a rate of \(2\) cm/sec and its area is increasing at a rate of \(4 \,\text{cm}^2\text{/sec}\). Find the rate at which the base of the triangle is changing when the height of the triangle is \(4\) cm and the area is \(20 \,\text{cm}^2\).
In exercises 25 - 27, consider an inverted right cone that is leaking water. (Inverted means the cone's point is facing down, like a funnel.) The dimensions of the conical tank are a height of 16 ft and a radius of 5 ft.
25) How fast does the depth of the water change when the water is \(10\) ft high if the cone leaks water at a rate of \(10 \,\text{ft}^3\text{/min}\)?
- Answer
- The depth of the water decreases at \(\frac{128}{125π}\) ft/min.
26) Find the rate at which the surface area of the water changes when the water is \(10\) ft high if the cone leaks water at a rate of \(10 \,\text{ft}^3\text{/min}\).
27) If the water level is decreasing at a rate of \(3\) in/min when the depth of the water is \(8\) ft, determine the rate at which water is leaking out of the cone.
- Answer
- The volume is decreasing at a rate of \(\frac{25π}{16}\,\text{ft}^3\text{/min}\).
28) A vertical cylinder is leaking water at a rate of \(1 \,\text{ft}^3\text{/sec}\). If the cylinder has a height of \(10\) ft and a radius of \(1\) ft, at what rate is the height of the water changing when the height is \(6\) ft?
29) A cylinder is leaking water but you are unable to determine at what rate. The cylinder has a height of \(2\) m and a radius of \(2\) m. Find the rate at which the water is leaking out of the cylinder if the rate at which the height is decreasing is \(10\) cm/min when the height is \(1\) m.
- Answer
- The water flows out at rate \(\frac{2π}{5}\,\text{m}^3\text{/min}\).
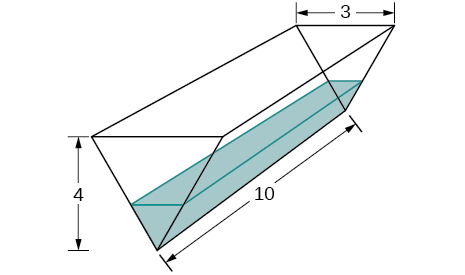
30) A trough has ends shaped like isosceles triangles, with width \(3\) m and height \(4\) m, and the trough is \(10\) m long. Water is being pumped into the trough at a rate of \(5\,\text{m}^3\text{/min}\). At what rate does the height of the water change when the water is \(1\) m deep?
31) A tank is shaped like an upside-down square pyramid, with base of \(4\) m by \(4\) m and a height of \(12\) m (see the following figure). How fast does the height increase when the water is \(2\) m deep if water is being pumped in at a rate of \(\frac{2}{3} \text{ m}^3\)/sec?
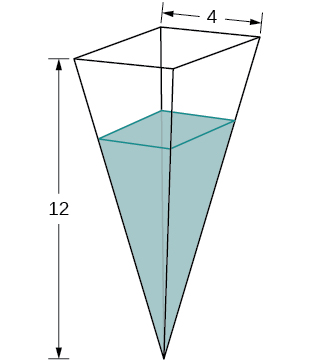
- Answer
- \(\frac{3}{2}\) m/sec
For exercises 32 - 34, consider a pool shaped like the bottom half of a sphere, that is being filled at a rate of \(25 \,\text{ft}^3\)/min. The radius of the pool is \(10\) ft.
32) Find the rate at which the depth of the water is changing when the water has a depth of \(5\) ft.
33) Find the rate at which the depth of the water is changing when the water has a depth of \(1\) ft.
- Answer
- \(\frac{25}{19π}\) ft/min
34) If the height is increasing at a rate of \(1\) in/sec when the depth of the water is \(2\) ft, find the rate at which water is being pumped in.
35) Gravel is being unloaded from a truck and falls into a pile shaped like a cone at a rate of \(10 \,\text{ft}^3/\text{min}\). The radius of the cone base is three times the height of the cone. Find the rate at which the height of the gravel changes when the pile has a height of \(5\) ft.
- Answer
- \(\frac{2}{45π}\) ft/min
36) Using a similar setup from the preceding problem, find the rate at which the gravel is being unloaded if the pile is \(5\) ft high and the height is increasing at a rate of \(4\) in/min.
In exercises 37 - 41, draw the situations and solve the related-rate problems.
37) You are stationary on the ground and are watching a bird fly horizontally at a rate of \(10\) m/sec. The bird is located \(40\) m above your head. How fast does the angle of elevation change when the horizontal distance between you and the bird is \(9\) m?
- Answer
- The angle decreases at \(\frac{400}{1681}\) rad/sec.
38) You stand \(40\) ft from a bottle rocket on the ground and watch as it takes off vertically into the air at a rate of \(20\) ft/sec. Find the rate at which the angle of elevation changes when the rocket is \(30\) ft in the air.
39) A lighthouse, \(L\), is on an island \(4\) mi away from the closest point, \(P\), on the beach (see the following image). If the lighthouse light rotates clockwise at a constant rate of \(10\) revolutions/min, how fast does the beam of light move across the beach \(2\) mi away from the closest point on the beach?
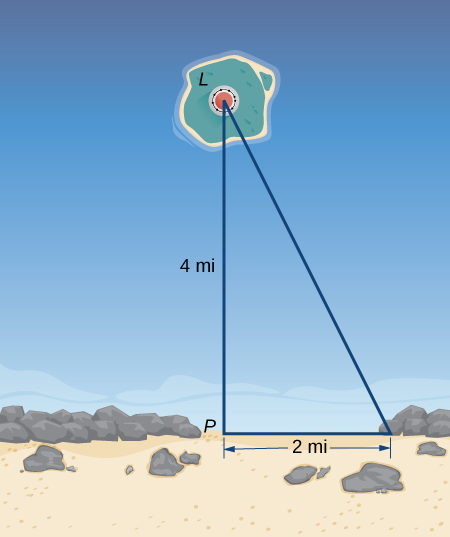
- Answer
- \(100π\) mi/min
40) Using the same setup as the previous problem, determine at what rate the beam of light moves across the beach \(1\) mi away from the closest point on the beach.
41) You are walking to a bus stop at a right-angle corner. You move north at a rate of \(2\) m/sec and are \(20\) m south of the intersection. The bus travels west at a rate of \(10\) m/sec away from the intersection – you have missed the bus! What is the rate at which the angle between you and the bus is changing when you are \(20\) m south of the intersection and the bus is \(10\) m west of the intersection?
- Answer
- The angle is changing at a rate of \(\frac{11}{25}\) rad/sec.
In exercises 42 - 45, refer to the figure of baseball diamond, which has sides of 90 ft.
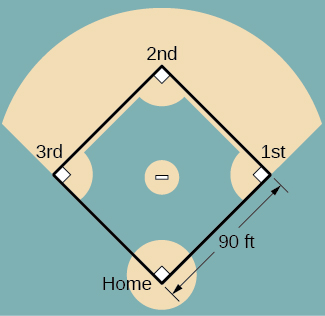
42) [T] A batter hits a ball toward third base at \(75\) ft/sec and runs toward first base at a rate of \(24\) ft/sec. At what rate does the distance between the ball and the batter change when \(2\) sec have passed?
43) [T] A batter hits a ball toward second base at \(80\) ft/sec and runs toward first base at a rate of \(30\) ft/sec. At what rate does the distance between the ball and the batter change when the runner has covered one-third of the distance to first base? (Hint: Recall the law of cosines.)
- Answer
- The distance is increasing at a rate of \(62.50\) ft/sec.
44) [T] A batter hits the ball and runs toward first base at a speed of \(22\) ft/sec. At what rate does the distance between the runner and second base change when the runner has run \(30\) ft?
45) [T] Runners start at first and second base. When the baseball is hit, the runner at first base runs at a speed of \(18\) ft/sec toward second base and the runner at second base runs at a speed of \(20\) ft/sec toward third base. How fast is the distance between runners changing 1 sec after the ball is hit?
- Answer
- The distance is decreasing at a rate of \(11.99\) ft/sec.

