3.9E: Exercises for Section 3.8
- Page ID
- 25950
In exercises 1 - 10, use implicit differentiation to find \(\dfrac{dy}{dx}\).
1) \(x^2−y^2=4\)
2) \(6x^2+3y^2=12\)
- Answer
- \(\dfrac{dy}{dx}=\dfrac{−2x}{y}\)
3) \(x^2y=y−7\)
4) \(3x^3+9xy^2=5x^3\)
- Answer
- \(\dfrac{dy}{dx}=\dfrac{x}{3y}−\dfrac{y}{2x}\)
5) \(xy−\cos(xy)=1\)
6) \(y\sqrt{x+4}=xy+8\)
- Answer
- \(\dfrac{dy}{dx}=\dfrac{y−\dfrac{y}{2\sqrt{x+4}}}{\sqrt{x+4}−x}\)
7) \(−xy−2=\frac{x}{7}\)
8) \(y\sin(xy)=y^2+2\)
- Answer
- \(\dfrac{dy}{dx}=\dfrac{y^2\cos(xy)}{2y−\sin(xy)−xy\cos(xy)}\)
9) \((xy)^2+3x=y^2\)
10) \(x^3y+xy^3=−8\)
- Answer
- \(\dfrac{dy}{dx}=\dfrac{−3x^2y−y^3}{x^3+3xy^2}\)
For exercises 11 - 16, find the equation of the tangent line to the graph of the given equation at the indicated point. Use a calculator or computer software to graph the function and the tangent line.
11) [T] \(x^4y−xy^3=−2, \quad (−1,−1)\)
12) [T] \(x^2y^2+5xy=14,\quad (2,1)\)
- Answer
-
\(y=−\frac{1}{2}x+2\)
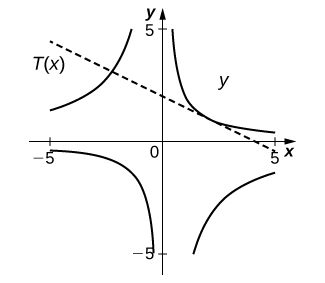
13) [T] \(\tan(xy)=y,\quad \left(\frac{π}{4},1\right)\)
14) [T] \(xy^2+\sin(πy)−2x^2=10, \quad (2,−3)\)
- Answer
-
\(y=\frac{1}{π+12}x−\frac{3π+38}{π+12}\)
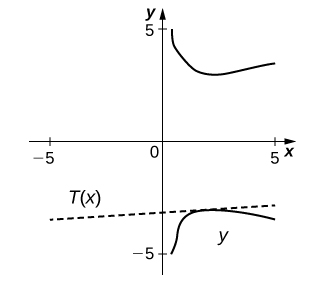
15) [T] \(\dfrac{x}{y}+5x−7=−\frac{3}{4}y, \quad (1,2)\)
16) [T] \(xy+\sin(x)=1,\quad \left(\frac{π}{2},0\right)\)
- Answer
-
\(y=0\)
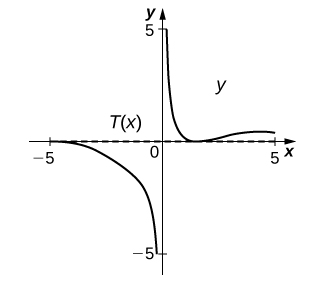
17) [T] The graph of a folium of Descartes with equation \(2x^3+2y^3−9xy=0\) is given in the following graph.
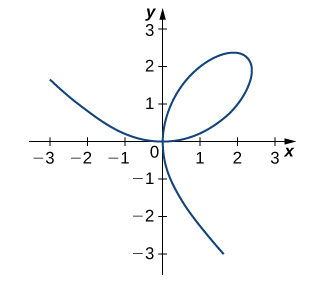
a. Find the equation of the tangent line at the point \((2,1)\). Graph the tangent line along with the folium.
b. Find the equation of the normal line to the tangent line in a. at the point \((2,1)\).
18) For the equation \(x^2+2xy−3y^2=0,\)
a. Find the equation of the normal to the tangent line at the point \((1,1)\).
b. At what other point does the normal line in a. intersect the graph of the equation?
- Answer
- a. \(y=−x+2\)
b. \((3,−1)\)
19) Find all points on the graph of \(y^3−27y=x^2−90\) at which the tangent line is vertical.
20) For the equation \(x^2+xy+y^2=7\),
a. Find the \(x\)-intercept(s).
b.Find the slope of the tangent line(s) at the \(x\)-intercept(s).
c. What does the value(s) in part b. indicate about the tangent line(s)?
- Answer
- a. \(\left(±\sqrt{7},0\right)\)
b. \(−2\)
c. They are parallel since the slope is the same at both intercepts.
21) Find the equation of the tangent line to the graph of the equation \(\sin^{−1}x+\sin^{−1}y=\frac{π}{6}\) at the point \(\left(0,\frac{1}{2}\right)\).
22) Find the equation of the tangent line to the graph of the equation \(\tan^{−1}(x+y)=x^2+\frac{π}{4}\) at the point \((0,1)\).
- Answer
- \(y=−x+1\)
23) Find \(y′\) and \(y''\) for \(x^2+6xy−2y^2=3\).
24) [T] The number of cell phones produced when \(x\) dollars is spent on labor and \(y\) dollars is spent on capital invested by a manufacturer can be modeled by the equation \(60x^{3/4}y^{1/4}=3240\).
a. Find \(\frac{dy}{dx}\) and evaluate at the point \((81,16)\).
b. Interpret the result of a.
- Answer
- a. \(\frac{dy}{dx}=−0.5926\)
b. When $81 is spent on labor and $16 is spent on capital, the amount spent on capital is decreasing by $0.5926 per $1 spent on labor.
25) [T] The number of cars produced when \(x\) dollars is spent on labor and \(y\) dollars is spent on capital invested by a manufacturer can be modeled by the equation \(30x^{1/3}y^{2/3}=360\).
(Both \(x\)and \(y\) are measured in thousands of dollars.)
a. Find \(\frac{dy}{dx}\) and evaluate at the point \((27,8)\).
b. Interpret the result of part a.
26) The volume of a right circular cone of radius \(x\) and height \(y\) is given by \(V=\frac{1}{3}πx^2y\). Suppose that the volume of the cone is \(85π\,\text{cm}^3\). Find \(\dfrac{dy}{dx}\) when \(x=4\) and \(y=16\).
- Answer
- \(\dfrac{dy}{dx} = −8\)
For exercises 27 - 28, consider a closed rectangular box with a square base with side \(x\) and height \(y\).
27) Find an equation for the surface area of the rectangular box, \(S(x,y)\).
28) If the surface area of the rectangular box is 78 square feet, find \(\dfrac{dy}{dx}\) when \(x=3\) feet and \(y=5\) feet.
- Answer
- \(\dfrac{dy}{dx} = −2.67\)
In exercises 29 - 31, use implicit differentiation to determine \(y′\). Does the answer agree with the formulas we have previously determined?
29) \(x=\sin y\)
30) \(x=\cos y\)
- Answer
- \(y′=−\dfrac{1}{\sqrt{1−x^2}}\)
31) \(x=\tan y\)

