6.3: Using the Normal Distribution
- Page ID
- 20381
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The shaded area in the following graph indicates the area to the left of \(x\). This area is represented by the probability \(P(X < x)\). Normal tables, computers, and calculators provide or calculate the probability \(P(X < x)\).
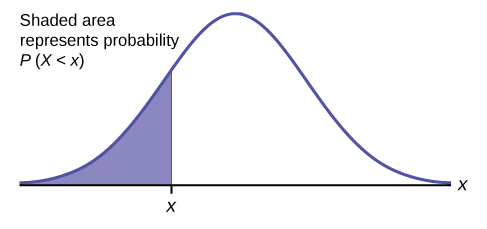
The area to the right is then \(P(X > x) = 1 – P(X < x)\). Remember, \(P(X < x) =\) Area to the left of the vertical line through \(x\). \(P(X < x) = 1 – P(X < x) =\) Area to the right of the vertical line through \(x\). \(P(X < x)\) is the same as \(P(X \leq x)\) and \(P(X > x)\) is the same as \(P(X \geq x)\) for continuous distributions.
Calculations of Probabilities
Probabilities are calculated using technology. There are instructions given as necessary for the TI-83+ and TI-84 calculators.
Online Normal Probability Calculator
Fill in all of the values except one below and hit Calculate then the last value will be given to you.
| Low: | High: | Mean: | Std. Dev.: | p= |
Example \(\PageIndex{1}\)
If the area to the left is 0.0228, then the area to the right is \(1 - 0.0228 = 0.9772\).
Exercise \(\PageIndex{1}\)
If the area to the left of \(x\) is \(0.012\), then what is the area to the right?
- Answer
-
\(1 - 0.012 = 0.988\)
Example \(\PageIndex{2}\)
The final exam scores in a statistics class were normally distributed with a mean of 63 and a standard deviation of five.
- Find the probability that a randomly selected student scored more than 65 on the exam.
- Find the probability that a randomly selected student scored less than 85.
- Find the 90th percentile (that is, find the score \(k\) that has 90% of the scores below k and 10% of the scores above \(k\)).
- Find the 70th percentile (that is, find the score \(k\) such that 70% of scores are below \(k\) and 30% of the scores are above \(k\)).
Answer
a. Let \(X\) = a score on the final exam. \(X \sim N(63, 5)\), where \(\mu = 63\) and \(\sigma = 5\)
Draw a graph.
Then, find \(P(x > 65)\).
\[P(x > 65) = 0.3446\nonumber \]
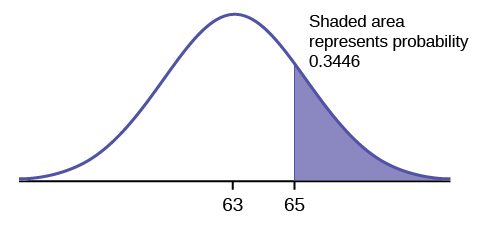
The probability that any student selected at random scores more than 65 is 0.3446.
For this problem, the right hand side is unbounded, going to infinity. It is safe to use 9999 for the high, since that will be many standard deviations above the mean. In general, for area that is unbounded from the right, use several 9's, where the number of 9's is two more than the number of digits of the largest number given. This gives \( P(x > 65) = 0.3446 \). We are calculating the area between 65 and 1099. In some instances, the lower number of the area might be unbounded. In that case, we similarly use -9999... where the number of 9's is two more than the number of digits of the largest number given.
Historical Note
The calculator calculates a \(z\)-score and then the probability from the \(z\)-score. Before technology, the \(z\)-score was looked up in a standard normal probability table (because the math involved is too cumbersome) to find the probability. In this example, a standard normal table with area to the left of the \(z\)-score was used. You calculate the \(z\)-score and look up the area to the left. The probability is the area to the right.
\[z = 65 – 63565 – 635 = 0.4\nonumber \]
Area to the left is 0.6554.
\[P(x > 65) = P(z > 0.4) = 1 – 0.6554 = 0.3446\nonumber \]
Calculate the \(z\)-score:
Here, we use the calculator to get the answer of 0.3999 which rounds to 0.4.
Answer
b. Draw a graph.
Then find \(P(x < 85)\), and shade the graph.
Using a computer or calculator, find \(P(x < 85) = 1\).
The probability that one student scores less than 85 is approximately one (or 100%).
Answer
c. Find the 90th percentile. For each problem or part of a problem, draw a new graph. Draw the \(x\)-axis. Shade the area that corresponds to the 90th percentile.
Let \(k =\) the 90th percentile. The variable \(k\) is located on the \(x\)-axis. \(P(x < k)\) is the area to the left of \(k\). The 90th percentile \(k\) separates the exam scores into those that are the same or lower than \(k\) and those that are the same or higher. Ninety percent of the test scores are the same or lower than \(k\), and ten percent are the same or higher. The variable \(k\) is often called a critical value.
\(k = 69.4\)
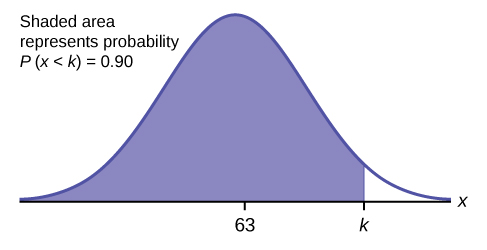
The 90th percentile is 69.4. This means that 90% of the test scores fall at or below 69.4 and 10% fall at or above. To get this answer on the calculator, the low is -9999, leave the high blank, the mean is 63, the standard deviation is 5 and p is 0.9. This gives 69.4.
Answer
d. Find the 70th percentile.
Draw a new graph and label it appropriately. \(k = 65.6\)
The 70th percentile is 65.6. This means that 70% of the test scores fall at or below 65.6 and 30% fall at or above.
Exercise \(\PageIndex{2}\)
The golf scores for a school team were normally distributed with a mean of 68 and a standard deviation of three. Find the probability that a randomly selected golfer scored less than 65.
- Answer
-
0.1587
Example \(\PageIndex{3}\)
A personal computer is used for office work at home, research, communication, personal finances, education, entertainment, social networking, and a myriad of other things. Suppose that the average number of hours a household personal computer is used for entertainment is two hours per day. Assume the times for entertainment are normally distributed and the standard deviation for the times is half an hour.
- Find the probability that a household personal computer is used for entertainment between 1.8 and 2.75 hours per day.
- Find the maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment.
Answer
a. Let \(X =\) the amount of time (in hours) a household personal computer is used for entertainment. \(X \sim N(2, 0.5)\) where \(\mu = 2\) and \(\sigma = 0.5\).
Find \(P(1.8 < x < 2.75)\).
The probability for which you are looking is the area between \(x = 1.8\) and \(x = 2.75\). \(P(1.8 < x < 2.75) = 0.5886\)
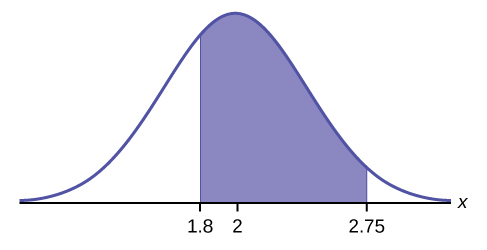
\[P(1.8 < x < 2.75) = 0.5886\]
The probability that a household personal computer is used between 1.8 and 2.75 hours per day for entertainment is 0.5886.
b.
To find the maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment, find the 25th percentile, \(k\), where \(P(x < k) = 0.25\).
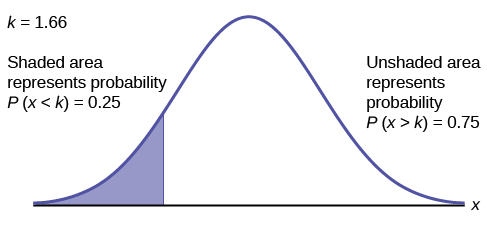
\[P(0.25 < x <2) = 1.66 \]
The maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment is 1.66 hours.
Exercise \(\PageIndex{3}\)
The golf scores for a school team were normally distributed with a mean of 68 and a standard deviation of three. Find the probability that a golfer scored between 66 and 70.
- Answer
-
\(P(66 < x <70) = 0.4950\)
Example \(\PageIndex{4}\)
There are approximately one billion smartphone users in the world today. In the United States the ages 13 to 55+ of smartphone users approximately follow a normal distribution with approximate mean and standard deviation of 36.9 years and 13.9 years, respectively.
- Determine the probability that a random smartphone user in the age range 13 to 55+ is between 23 and 64.7 years old.
- Determine the probability that a randomly selected smartphone user in the age range 13 to 55+ is at most 50.8 years old.
- Find the 80th percentile of this distribution, and interpret it in a complete sentence.
Answer
a. \(P(23 < x < 64.7 = 0.8186\)
b. \( P(-9999 < x < 50.8) = 0.8413\)
c. The 80th percentile is 48.6 years.
80% of the smartphone users in the age range 13 – 55+ are 48.6 years old or less.
Use the information in Example to answer the following questions.
Exercise \(\PageIndex{4}\)
- Find the 30th percentile, and interpret it in a complete sentence.
- What is the probability that the age of a randomly selected smartphone user in the range 13 to 55+ is less than 27 years old and at least 0 years old?
- Answer
-
Let \(X =\) a smart phone user whose age is 13 to 55+. \(X \sim N(36.9, 13.9)\)
To find the 30th percentile, find \(k\) such that \(P(x < k) = 0.30\).
Thirty percent of smartphone users 13 to 55+ are at most 29.6 years and 70% are at least 29.6 years. Find \(P(x < 27)\)
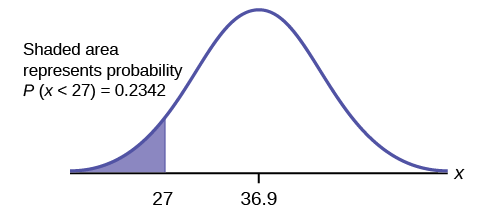
\[P(0 < x < 27) = 0.2342 \]
Example \(\PageIndex{5}\)
There are approximately one billion smartphone users in the world today. In the United States the ages 13 to 55+ of smartphone users approximately follow a normal distribution with approximate mean and standard deviation of 36.9 years and 13.9 years respectively. Using this information, answer the following questions (round answers to one decimal place).
- Calculate the interquartile range (\(IQR\)).
- Forty percent of the ages that range from 13 to 55+ are at least what age?
Answer
a.
\[IQR = Q_{3} – Q_{1} \]
Calculate \(Q_{3} =\) 75th percentile and \(Q_{1} =\) 25th percentile.
\[ Q_{3} = 46.2754 \]
\[ Q_{1} = 27.5246 \]
\[IQR = Q_{3} - Q_{1} = 18.7508 \]
b.
Find \(k\) where \(P(x > k) = 0.40\) ("At least" translates to "greater than or equal to.")
\(0.40 =\) the area to the right.
Area to the left \(= 1 – 0.40 = 0.60\).
The area to the left of \(k = 0.60\).
\(P(0.60 < x < 36.9) = 40.4215\).
\(k = 40.42\).
Forty percent of the ages that range from 13 to 55+ are at least 40.42 years.
Exercise \(\PageIndex{5}\)
Two thousand students took an exam. The scores on the exam have an approximate normal distribution with a mean \(\mu = 81\) points and standard deviation \(\sigma = 15\) points.
- Calculate the first- and third-quartile scores for this exam.
- The middle 50% of the exam scores are between what two values?
Answer
- \(Q_{1} =\) 25th percentile \( = 70.9\)
\(Q_{3} =\) 75th percentile \( = 91.1\) - The middle 50% of the scores are between 70.9 and 91.1.
Example \(\PageIndex{6}\)
A citrus farmer who grows mandarin oranges finds that the diameters of mandarin oranges harvested on his farm follow a normal distribution with a mean diameter of 5.85 cm and a standard deviation of 0.24 cm.
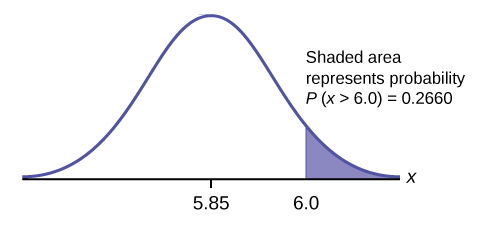
- Find the probability that a randomly selected mandarin orange from this farm has a diameter larger than 6.0 cm. Sketch the graph.
- The middle 20% of mandarin oranges from this farm have diameters between ______ and ______.
- Find the 90th percentile for the diameters of mandarin oranges, and interpret it in a complete sentence.
Answer
a. \(P(6 < x < 999) = 0.2660\)
Answer
b.
\(1 – 0.20 = 0.80\)
The tails of the graph of the normal distribution each have an area of 0.40.
Find \(k1\), the 40th percentile, and \(k2\), the 60th percentile (\(0.40 + 0.20 = 0.60\)).
\(k1 = 5.79\) cm
\(k2 = 5.91\) cm
Answer
c. 6.16: Ninety percent of the diameter of the mandarin oranges is at most 6.15 cm.
Exercise \(\PageIndex{6}\)
Using the information from Example, answer the following:
- The middle 40% of mandarin oranges from this farm are between ______ and ______.
- Find the probability that a randomly selected mandarin orange from this farm has a diameter larger than 5 cm.
- Answer a
-
The middle area \(= 0.40\), so each tail has an area of 0.30.
\( – 0.40 = 0.60\)
The tails of the graph of the normal distribution each have an area of 0.30.
Find \(k1\), the 30th percentile and \(k2\), the 70th percentile (\(0.40 + 0.30 = 0.70\)).
\(k1 = 5.72\) cm
\(k2 = 5.98\) cm
- Answer b
-
\(P(5 < x < 999) = 0.9998\)
References
- “Naegele’s rule.” Wikipedia. Available online at http://en.Wikipedia.org/wiki/Naegele's_rule (accessed May 14, 2013).
- “403: NUMMI.” Chicago Public Media & Ira Glass, 2013. Available online at http://www.thisamericanlife.org/radi...sode/403/nummi (accessed May 14, 2013).
- “Scratch-Off Lottery Ticket Playing Tips.” WinAtTheLottery.com, 2013. Available online at http://www.winatthelottery.com/publi...partment40.cfm (accessed May 14, 2013).
- “Smart Phone Users, By The Numbers.” Visual.ly, 2013. Available online at http://visual.ly/smart-phone-users-numbers (accessed May 14, 2013).
- “Facebook Statistics.” Statistics Brain. Available online at http://www.statisticbrain.com/facebo...tics/(accessed May 14, 2013).
Chapter Review
The normal distribution, which is continuous, is the most important of all the probability distributions. Its graph is bell-shaped. This bell-shaped curve is used in almost all disciplines. Since it is a continuous distribution, the total area under the curve is one. The parameters of the normal are the mean \(\mu\) and the standard deviation σ. A special normal distribution, called the standard normal distribution is the distribution of z-scores. Its mean is zero, and its standard deviation is one.
Formula Review
- Normal Distribution: \(X \sim N(\mu, \sigma)\) where \(\mu\) is the mean and σ is the standard deviation.
- Standard Normal Distribution: \(Z \sim N(0, 1)\).
Exercise 6.3.7
How would you represent the area to the left of one in a probability statement?
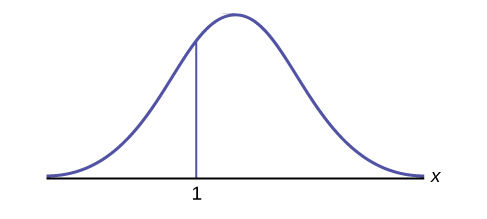
Answer
\(P(x < 1)\)
Exercise 6.3.8
Is \(P(x < 1)\) equal to \(P(x \leq 1)\)? Why?
Answer
Yes, because they are the same in a continuous distribution: \(P(x = 1) = 0\)
Exercise 6.3.9
How would you represent the area to the left of three in a probability statement?
Exercise 6.3.10
What is the area to the right of three?

Answer
\(1 – P(x < 3)\) or \(P(x > 3)\)
Exercise 6.3.11
If the area to the left of \(x\) in a normal distribution is 0.123, what is the area to the right of \(x\)?
Exercise 6.3.12
If the area to the right of \(x\) in a normal distribution is 0.543, what is the area to the left of \(x\)?
Answer
\(1 - 0.543 = 0.457\)
Use the following information to answer the next four exercises:
\(X \sim N(54, 8)\)
Exercise 6.3.13
Find the probability that \(x > 56\).
Exercise 6.3.14
Find the probability that \(x < 30\).
Answer
0.0013
Exercise 6.3.15
Find the 80th percentile.
Exercise 6.3.16
Find the 60th percentile.
Answer
56.03
Exercise 6.3.17
\(X \sim N(6, 2)\)
Find the probability that \(x\) is between three and nine.
Exercise 6.3.18
\(X \sim N(–3, 4)\)
Find the probability that \(x\) is between one and four.
Answer
0.1186
Exercise 6.3.19
\(X \sim N(4, 5)\)
Find the maximum of \(x\) in the bottom quartile.
Exercise 6.3.20
Use the following information to answer the next three exercise: The life of Sunshine CD players is normally distributed with a mean of 4.1 years and a standard deviation of 1.3 years. A CD player is guaranteed for three years. We are interested in the length of time a CD player lasts. Find the probability that a CD player will break down during the guarantee period.
- Sketch the situation. Label and scale the axes. Shade the region corresponding to the probability.
Figure \(\PageIndex{12}\).
\(P(0 < x <\) ____________\() =\) ___________ (Use zero for the minimum value of \(x\).)
Answer
- Check student’s solution.
- 3, 0.1979
Exercise 6.3.21
Find the probability that a CD player will last between 2.8 and six years.
- Sketch the situation. Label and scale the axes. Shade the region corresponding to the probability.

Figure \(\PageIndex{13}\).
\(P(\)__________ \(< x <\) __________\()\) = __________
Exercise 6.3.22
Find the 70th percentile of the distribution for the time a CD player lasts.
- Sketch the situation. Label and scale the axes. Shade the region corresponding to the lower 70%.

Figure \(\PageIndex{14}\).
\(P(x < k) =\) __________ Therefore, \(k =\) _________
Answer
- Check student’s solution.
- 0.70, 4.78 years
Contributors and Attributions
Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/30189442-699...b91b9de@18.114.


