5.2: Partioning the Sums of Squares

Time to partition the sums of squares again. Remember the act of partitioning, or splitting up, the variance is the core idea of ANOVA. To continue using the house analogy, our total sums of squares (SS Total) is our big empty house. We want to split it up into little rooms. Before in the between-subjects ANOVA, we partitioned SS Total using this formula:

\[SS_\text{TOTAL} = SS_\text{Effect} + SS_\text{Error} \nonumber \]

The \(SS_\text{Effect}\) was the variance we could attribute to the means of the different groups, and \(SS_\text{Error}\) was the leftover variance that we couldn’t explain. \(SS_\text{Effect}\) and \(SS_\text{Error}\) are the partitions of \(SS_\text{TOTAL}\), they are the little rooms.

In the between-subjects ANOVA above, we got to split \(SS_\text{TOTAL}\) into two parts. What is most interesting about the repeated-measures design, is that we get to split \(SS_\text{TOTAL}\) into three parts, there’s one more partition. Can you guess what the new partition is? Hint: whenever we have a new way to calculate means in our design, we can always create a partition for those new means. What are the new means in the repeated measures design?

Here is the formula for partitioning \(SS_\text{TOTAL}\) in a repeated-measures ANOVA:

\[SS_\text{TOTAL} = SS_\text{Effect} + SS_\text{Subjects} +SS_\text{Error} \nonumber \]

We’ve added \(SS_\text{Subjects}\) as the new idea in the formula. What’s the idea here? Well, because each subject or participant was measured in each condition, we have a new set of means. These are the means for each subject or participant, collapsed across the conditions. For example, subject 1 has a mean (mean of their scores in conditions A, B, and C); subject 2 has a mean (mean of their scores in conditions A, B, and C); and subject 3 has a mean (mean of their scores in conditions A, B, and C). There are three subject means, one for each subject, collapsed across the conditions. And, we can now estimate the portion of the total variance that is explained by these subject means.

Before we go into the calculations, it's important to pause and compare the differences of how the sum of squares are partitioned in between-subjects ANOVA vs. within-subjects ANOVA.

Recall, in between-subjects ANOVA, we use different words to describe parts of the ANOVA (which can be really confusing). For example, we described the SS formula for a between-subjects ANOVA like this:

\[SS_\text{TOTAL} = SS_\text{Effect} + SS_\text{Error} \nonumber \]

The very same formula is often written differently, using the words between and within in place of effect and error, it looks like this:

\[SS_\text{TOTAL} = SS_\text{Between} + SS_\text{Within} \nonumber \]

Here, \(SS_\text{Between}\) (which we have been calling \(SS_\text{Effect}\)) refers to variation between the group means, that’s why it is called \(SS_\text{Between}\). Second, and most important, \(SS_\text{Within}\) (which we have been calling \(SS_\text{Error}\)), refers to the leftover variation within each group mean. Specifically, it is the variation between each group mean and each score within that group. Remember, for each group mean, every score is probably off a little bit from the mean. So, the scores within each group have some variation. This is the within group variation, and it is why the leftover error that we can’t explain is often called \(SS_\text{Within}\).

Perhaps a picture will help to clear things up.

Figure \(\PageIndex{1}\): Illustration showing how the total sums of squares are partitioned differently for a between versus repeated-measures design.

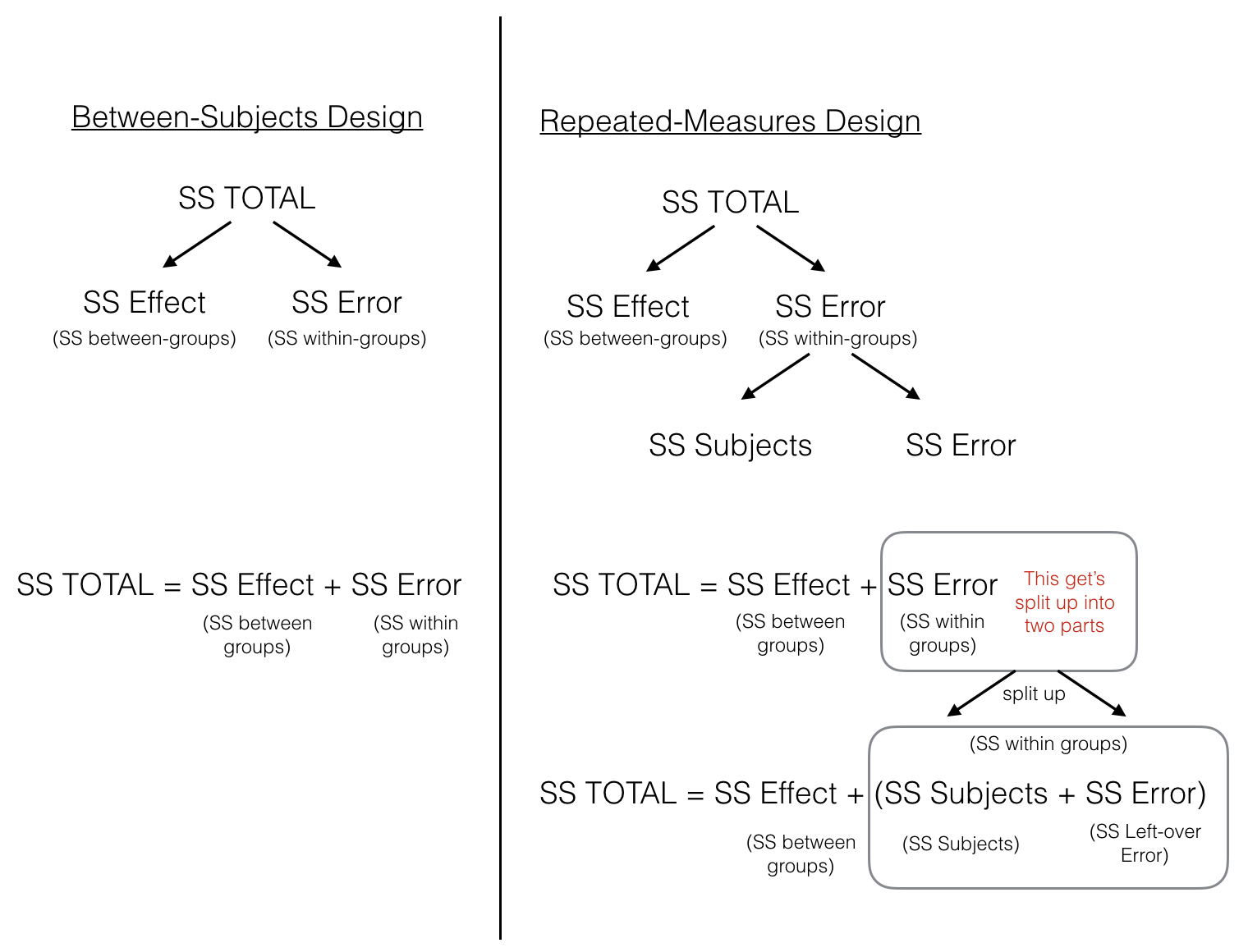
The figure lines up the partitioning of the Sums of Squares for both between-subjects and repeated-measures designs. In both designs, \(SS_\text{Total}\) is first split up into two pieces \(SS_\text{Effect (between-groups)}\) and \(SS_\text{Error (within-groups)}\). At this point, both ANOVAs are the same. In the repeated measures case we split the \(SS_\text{Error (within-groups)}\) into two more littler parts, which we call \(SS_\text{Subjects (error variation about the subject mean)}\) and \(SS_\text{Error (left-over variation we can't explain)}\).

The critical feature of the repeated-measures ANOVA, is that the \(SS_\text{Error}\) that we will later use to compute the MS (Mean Squared) in the denominator for the \(F\)-value, is smaller in a repeated-measures design, compared to a between subjects design. This is because the \(SS_\text{Error (within-groups)}\) is split into two parts, \(SS_\text{Subjects (error variation about the subject mean)}\) and \(SS_\text{Error (left-over variation we can't explain)}\).

To make this more clear, here is another figure:

Figure \(\PageIndex{2}\): Close-up showing that the Error term is split into two parts in the repeated measures design.

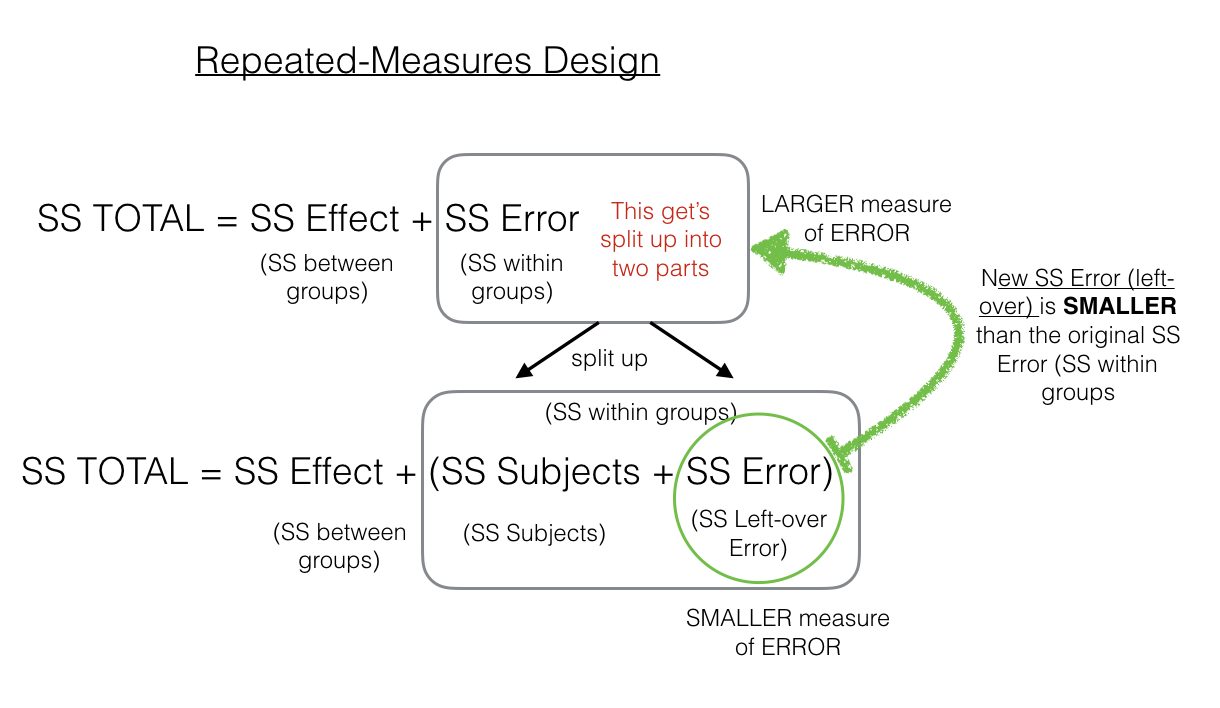
As we point out, the \(SS_\text{Error (left-over)}\) in the green circle will be a smaller number than the \(SS_\text{Error (within-group)}\). That’s because we are able to subtract out the \(SS_\text{Subjects}\) part of the \(SS_\text{Error (within-group)}\). This can have the effect of producing larger F-values when using a repeated-measures design compared to a between-subjects design, which is more likely to yield smaller P obtained values and allow us to reject the null hypothesis.