11.3: Analysis of Variance (ANOVA)

There are times where you want to compare three or more population means. One idea is to just test different combinations of two means. The problem with that is that your chance for a type I error increases. Instead you need a process for analyzing all of them at the same time. This process is known as analysis of variance (ANOVA). The test statistic for the ANOVA is fairly complicated, you will want to use technology to find the test statistic and p-value. The test statistic is distributed as an F-distribution, which is skewed right and depends on degrees of freedom. Since you will use technology to find these, the distribution and the test statistic will not be presented. Remember, all hypothesis tests are the same process. Note that to obtain a statistically significant result there need only be a difference between any two of the k means.

Before conducting the hypothesis test, it is helpful to look at the means and standard deviations for each data set. If the sample means with consideration of the sample standard deviations are different, it may mean that some of the population means are different. However, do realize that if they are different, it doesn’t provide enough evidence to show the population means are different. Calculating the sample statistics just gives you an idea that conducting the hypothesis test is a good idea.

Hypothesis test using ANOVA to compare k means

1. State the random variables and the parameters in words
   \(\begin{array}{l}{x_{1}=\text { random variable } 1} \\ {x_{2}=\text { random variable } 2} \\ {\vdots} \\ {x_{k}=\text { random variable } k} \\ {\mu_{1}=\text { mean of random variable } 2} \\ {\begin{array}{l}{\mu_{2}=\text { mean of random variable } 2} \\ {\vdots} \\ {\mu_{k}=\text { mean of random variable } k}\end{array}}\end{array}\)
2. State the null and alternative hypotheses and the level of significance
   \(H_{o} : \mu_{1}=\mu_{2}=\mu_{3}=\cdots=\mu_{k}\)
   \(H_{A}\) : at least two of the means are not equal
   Also, state your \(\alpha\) level here.
3. State and check the assumptions for the hypothesis test
   1. A random sample of size \(n_{i}\) is taken from each population.
   2. All the samples are independent of each other.
   3. Each population is normally distributed. The ANOVA test is fairly robust to the assumption especially if the sample sizes are fairly close to each other. Unless the populations are really not normally distributed and the sample sizes are close to each other, then this is a loose assumption.
   4. The population variances are all equal. If the sample sizes are close to each other, then this is a loose assumption.
4. . Find the test statistic and p-value
   The test statistic is \(F=\dfrac{M S_{B}}{M S_{W}}\), where \(M S_{B}=\dfrac{S S_{B}}{d f_{B}}\) is the mean square between the groups (or factors), and \(M S_{W}=\dfrac{S S_{W}}{d f_{W}}\) is the mean square within the groups. The degrees of freedom between the groups is \(d f_{B}=k-1\) and the degrees of freedom within the groups is \(d f_{W}=n_{1}+n_{2}+\cdots+n_{k}-k\). To find all of the values, use technology such as the TI-83/84 calculator or R.
   The test statistic, F, is distributed as an F-distribution, where both degrees of freedom are needed in this distribution. The p-value is also calculated by the calculator or R.
5. Conclusion
   This is where you write reject \(H_{o}\) or fail to reject \(H_{o}\). The rule is: if the p-value < \(\alpha\), then reject \(H_{o}\). If the p-value \(\geq \alpha\), then fail to reject \(H_{o}\).
6. Interpretation
   This is where you interpret in real world terms the conclusion to the test. The conclusion for a hypothesis test is that you either have enough evidence to show \(H_{A}\) is true, or you do not have enough evidence to show \(H_{A}\) is true.

If you do in fact reject \(H_{o}\), then you know that at least two of the means are different. The next question you might ask is which are different? You can look at the sample means, but realize that these only give a preliminary result. To actually determine which means are different, you need to conduct other tests. Some of these tests are the range test, multiple comparison tests, Duncan test, Student-Newman-Keuls test, Tukey test, Scheffé test, Dunnett test, least significant different test, and the Bonferroni test. There is no consensus on which test to use. These tests are available in statistical computer packages such as Minitab and SPSS.

Example \(\PageIndex{1}\) hypothesis test involving several means

Cancer is a terrible disease. Surviving may depend on the type of cancer the person has. To see if the mean survival time for several types of cancer are different, data was collected on the survival time in days of patients with one of these cancer in advanced stage. The data is in Example \(\PageIndex{1}\) ("Cancer survival story," 2013). (Please realize that this data is from 1978. There have been many advances in cancer treatment, so do not use this data as an indication of survival rates from these cancers.) Do the data indicate that at least two of the mean survival time for these types of cancer are not all equal? Test at the 1% level.

Table \(\PageIndex{1}\): Survival Times in Days of Five Cancer Types

Stomach	Bronchus	Colon	Ovary	Breast
124	81	248	1234	1235
42	461	377	89	24
25	20	189	201	1581
45	450	1843	356	1166
412	246	180	2970	40
51	166	537	456	727
1112	63	519		3808
46	64	455		791
103	155	406		1804
876	859	365		3460
146	151	942		719
340	166	776
396	37	372
	223	163
	138	101
	72	20
	245	283

Solution

1. State the random variables and the parameters in words

\(\begin{array}{l}{x_{1}=\text { survival time from stomach cancer }} \\ {x_{2}=\text { survival time from bronchus cancer }} \\ {x_{3}=\text { survival time from colon cancer }} \\ {x_{4}=\text { survival time from ovarian cancer }} \\ {x_{5}=\text { survival time from breast cancer }} \\ {\mu_{1}=\text { mean survival time from breast cancer }} \\ {\mu_{1}=\text { mean survival time from bronchus cancer }} \\ {\mu_{3}=\text { mean survival time from colon cancer }} \\ {\mu_{4} = \text{mean survival time from ovarian cancer}}\\{\mu_{5} = \text{mean survival time from breast cancer}}\end{array}\)

Now before conducting the hypothesis test, look at the means and standard deviations.

\(\begin{array}{ll}{\overline{x}_{1}= 286}&{s_{1}\approx 346.31}\\{\overline{x}_{2} \approx 211.59} & {s_{2} \approx 209.86} \\ {\overline{x}_{3} \approx 457.41} & {s_{3} \approx 427.17} \\ {\overline{x}_{4} \approx 884.33} & {s_{4} \approx 1098.58} \\ {\overline{x}_{5} \approx 1395.91} & {s_{5} \approx 1238.97}\end{array}\)

There appears to be a difference between at least two of the means, but realize that the standard deviations are very different. The difference you see may not be significant.

Notice the sample sizes are not the same. The sample sizes are

\(n_{1}=13, n_{2}=17, n_{3}=17, n_{4}=6, n_{5}=11\)

2. State the null and alternative hypotheses and the level of significance

\(H_{o} : \mu_{1}=\mu_{2}=\mu_{3}=\mu_{4}=\mu_{5}\)

\(H_{A}\) : at least two of the means are not equal

\(\alpha\) = 0.01

3. State and check the assumptions for the hypothesis test

1. A random sample of 13 survival times from stomach cancer was taken. A random sample of 17 survival times from bronchus cancer was taken. A random sample of 17 survival times from colon cancer was taken. A random sample of 6 survival times from ovarian cancer was taken. A random sample of 11 survival times from breast cancer was taken. These statements may not be true. This information was not shared as to whether the samples were random or not but it may be safe to assume that.
2. Since the individuals have different cancers, then the samples are independent.
3. Population of all survival times from stomach cancer is normally distributed.
   Population of all survival times from bronchus cancer is normally distributed.
   Population of all survival times from colon cancer is normally distributed.
   Population of all survival times from ovarian cancer is normally distributed.
   Population of all survival times from breast cancer is normally distributed.
   Looking at the histograms, box plots and normal quantile plots for each sample, it appears that none of the populations are normally distributed. The sample sizes are somewhat different for the problem. This assumption may not be true.
4. The population variances are all equal. The sample standard deviations are approximately 346.3, 209.9, 427.2, 1098.6, and 1239.0 respectively. This assumption does not appear to be met, since the sample standard deviations are very different. The sample sizes are somewhat different for the problem. This assumption may not be true.

4. Find the test statistic and p-value

To find the test statistic and p-value using the TI-83/84, type each data set into L1 through L5. Then go into STAT and over to TESTS and choose ANOVA(. Then type in L1,L2,L3,L4,L5 and press enter. You will get the results of the ANOVA test.

Figure \(\PageIndex{1}\): Setup for ANOVA on TI-83/84

Figure \(\PageIndex{2}\): Results of ANOVA on TI-83/84

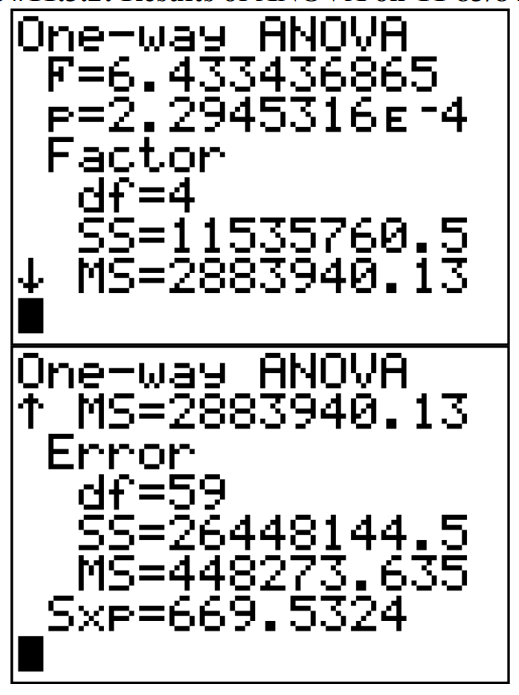
The test statistic is \(F \approx 6.433\) and \(p-\text { value } \approx 2.29 \times 10^{-4}\)

Just so you know, the Factor information is between the groups and the Error is within the groups. So

\(\begin{array}{l}{M S_{B} \approx 2883940.13, S S_{B} \approx 11535760.5, \text { and } d f_{B}=4 \text { and }} \\ {M S_{W} \approx 448273.635, S S_{W} \approx 448273.635, \text { and } d f_{W}=59}\end{array}\)

To find the test statistic and p-value on R:
The commands would be:
variable=c(type in all data values with commas in between) – this is the response variable
factor=c(rep("factor 1", number of data values for factor 1), rep("factor 2", number of data values for factor 2), etc) – this separates the data into the different factors that the measurements were based on.
data_name = data.frame(variable, factor) – this puts the data into one variable. data_name is the name you give this variable
aov(variable ~ factor, data = data name) – runs the ANOVA analysis

For this example, the commands would be:
time=c(124, 42, 25, 45, 412, 51, 1112, 46, 103, 876, 146, 340, 396, 81, 461, 20, 450, 246, 166, 63, 64, 155, 859, 151, 166, 37, 223, 138, 72, 245, 248, 377, 189, 1843, 180, 537, 519, 455, 406, 365, 942, 776, 372, 163, 101, 20, 283, 1234, 89, 201, 356, 2970, 456, 1235, 24, 1581, 1166, 40, 727, 3808, 791, 1804, 3460, 719)
factor=c(rep("Stomach", 13), rep("Bronchus", 17), rep("Colon", 17), rep("Ovary", 6), rep("Breast", 11))
survival=data.frame(time, factor)
results=aov(time~factor, data=survival)
summary(results)

\(\begin{array}{cccccc}{}&{\text{Df}}&{\text{Sum Sq}}&{\text{Mean Sq}}&{\text{F value}}&{\text{Pr(>F)}}\\{\text{factor}}&{4}&{11535761}&{2883940}&{6.4333}&{0.000229***}\\{\text{Residuals}}&{59}&{26448144}&{448274} \end{array}\)

---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

The test statistic is F = 6.433 and the p-value = 0.000229.

5. Conclusion

Reject \(H_{o}\) since the p-value is less than 0.01.

6. Interpretation

There is evidence to show that at least two of the mean survival times from different cancers are not equal.

By examination of the means, it appears that the mean survival time for breast cancer is different from the mean survival times for both stomach and bronchus cancers. It may also be different for the mean survival time for colon cancer. The others may not be different enough to actually say for sure.

Homework

Exercise \(\PageIndex{1}\)

In each problem show all steps of the hypothesis test. If some of the assumptions are not met, note that the results of the test may not be correct and then continue the process of the hypothesis test.

1. Cuckoo birds are in the habit of laying their eggs in other birds’ nest. The other birds adopt and hatch the eggs. The lengths (in cm) of cuckoo birds’ eggs in the other species nests were measured and are in Example \(\PageIndex{2}\) ("Cuckoo eggs in," 2013). Do the data show that the mean length of cuckoo bird’s eggs is not all the same when put into different nests? Test at the 5% level.

   Table \(\PageIndex{2}\): Lengths of Cuckoo Bird Eggs in Different Species Nests

   Meadow Pipit		Tree Pipit	Hedge Sparrow	Robin	Pied Wagtail	Wren
   19.65	22.25	21.05	20.85	21.05	21.05	19.85
   20.05	22.25	21.85	21.65	21.85	21.85	20.05
   20.65	22.25	22.05	22.05	22.05	21.85	20.25
   20.85	22.25	22.45	22.85	22.05	21.85	20.85
   21.65	22.65	22.65	23.05	22.05	22.05	20.85
   21.65	22.65	23.25	23.05	22.25	22.45	20.85
   21.65	22.85	23.25	23.05	22.45	22.65	21.05
   21.85	22.85	23.25	23.05	22.45	23.05	21.05
   21.85	22.85	23.45	23.45	22.65	23.05	21.05
   21.85	22.85	23.45	23.85	23.05	23.25	21.25
   22.05	23.05	23.65	23.85	23.05	23.45	21.45
   22.05	23.25	23.85	23.85	23.05	24.05	22.05
   22.05	23.25	24.05	24.05	23.05	24.05	22.05
   22.05	23.45	24.05	25.05	23.05	24.05	22.05
   22.05	23.65	24.05		23.25	24.85	22.25
   22.05	23.85			23.85
   22.05	24.25
   22.05	24.45
   22.05	22.25
   22.05	22.25
   22.25	22.25
   22.25	22.25
   22.25

2. Levi-Strauss Co manufactures clothing. The quality control department measures weekly values of different suppliers for the percentage difference of waste between the layout on the computer and the actual waste when the clothing is made (called run-up). The data is in Example \(\PageIndex{3}\), and there are some negative values because sometimes the supplier is able to layout the pattern better than the computer ("Waste run up," 2013). Do the data show that there is a difference between some of the suppliers? Test at the 1% level.

    

   Table \(\PageIndex{3}\): Run-ups for Different Plants Making Levi Strauss Clothing

   Plant 1	Plant 2	Plant 3	Plant 4	Plant 5
   1.2	16.4	12.1	11.5	24
   10.1	-6	9.7	10.2	-3.7
   -2	-11.6	7.4	3.8	8.2
   1.5	-1.3	-2.1	8.3	9.2
   -3	4	10.1	6.6	-9.3
   -0.7	17	4.7	10.2	8
   3.2	3.8	4.6	8.8	15.8
   2.7	4.3	3.9	2.7	22.3
   -3.2	10.4	3.6	5.1	3.1
   -1.7	4.2	9.6	11.2	16.8
   2.4	8.5	9.8	5.9	11.3
   0.3	6.3	6.5	13	12.3
   3.5	9	5.7	6.8	16.9
   -0.8	7.1	5.1	14.5
   19.4	4.3	3.4	5.2
   2.8	19.7	-0.8	7.3
   13	3	-3.9	7.1
   42.7	7.6	0.9	3.4
   1.4	70.2	1.5	0.7
   3	8.5
   2.4	6
   1.3	2.9

3. Several magazines were grouped into three categories based on what level of education of their readers the magazines are geared towards: high, medium, or low level. Then random samples of the magazines were selected to determine the number of three-plus-syllable words were in the advertising copy, and the data is in Example \(\PageIndex{4}\) ("Magazine ads readability," 2013). Is there enough evidence to show that the mean number of three-plus-syllable words in advertising copy is different for at least two of the education levels? Test at the 5% level.

    

   Table \(\PageIndex{4}\): Number of Three Plus Syllable Words in Advertising Copy

   High Education	Medium Education	Low Education
   34	13	7
   21	22	7
   37	25	7
   31	3	7
   10	5	7
   24	2	7
   39	9	8
   10	3	8
   17	0	8
   18	4	8
   32	29	8
   17	26	8
   3	5	9
   10	5	9
   6	24	9
   5	15	9
   6	3	9
   6	8	9

4. A study was undertaken to see how accurate food labeling for calories on food that is considered reduced calorie. The group measured the amount of calories for each item of food and then found the percent difference between measured and labeled food, \(\dfrac{(\text { measured - labeled })}{\text { labeled }} * 100 \%\). The group also looked at food that was nationally advertised, regionally distributed, or locally prepared. The data is in Example \(\PageIndex{5}\) ("Calories datafile," 2013). Do the data indicate that at least two of the mean percent differences between the three groups are different? Test at the 10% level.

    

   Table \(\PageIndex{5}\): Percent Differences Between Measured and Labeled Food

   National Advertised	Regionally Advertised	Locally Prepared
   2	41	15
   -28	46	60
   -6	2	250
   8	25	145
   6	39	6
   -1	16.5	8-
   1-	17	95
   13	28	3
   15	-3
   -4	14
   -4	34
   -18	42
   10
   5
   3
   -7
   3
   -0.5
   -10
   6

5. The amount of sodium (in mg) in different types of hotdogs is in Example \(\PageIndex{6}\) ("Hot dogs story," 2013). Is there sufficient evidence to show that the mean amount of sodium in the types of hotdogs are not all equal? Test at the 5% level.

    

   Table \(\PageIndex{6}\): Amount of Sodium (in mg) in Beef, Meat, and Poultry Hotdogs

   Beef	Meat	Poultry
   495	458	430
   477	506	375
   425	473	396
   322	545	383
   482	496	387
   587	360	542
   370	387	359
   322	386	357
   479	507	528
   375	393	513
   330	405	426
   300	372	513
   386	144	358
   401	511	581
   645	405	588
   440	428	522
   317	339	545
   319
   298
   253

Answer

For all hypothesis tests, just the conclusion is given. See solutions for the entire answer.

1. Reject Ho

3. Reject Ho

5. Fail to reject Ho

Data Source:

Aboriginal deaths in custody. (2013, September 26). Retrieved from http://www.statsci.org/data/oz/custody.html

Activities of dolphin groups. (2013, September 26). Retrieved from http://www.statsci.org/data/general/dolpacti.html

Boyle, P., Flowerdew, R., & Williams, A. (1997). Evaluating the goodness of fit in models of sparse medical data: A simulation approach. International Journal of Epidemiology, 26(3), 651-656. Retrieved from http://ije.oxfordjournals.org/conten...3/651.full.pdf html

Calories datafile. (2013, December 07). Retrieved from lib.stat.cmu.edu/DASL/Datafiles/Calories.html

Cancer survival story. (2013, December 04). Retrieved from lib.stat.cmu.edu/DASL/Stories...rSurvival.html

Car preferences. (2013, September 26). Retrieved from http://www.statsci.org/data/oz/carprefs.html

Cuckoo eggs in nest of other birds. (2013, December 04). Retrieved from lib.stat.cmu.edu/DASL/Stories/cuckoo.html

Education by age datafile. (2013, December 05). Retrieved from lib.stat.cmu.edu/DASL/Datafil...tionbyage.html

Encyclopedia Titanica. (2013, November 09). Retrieved from www.encyclopediatitanica.org/

Global health observatory data respository. (2013, October 09). Retrieved from http://apps.who.int/gho/athena/data/...t=GHO/MORT_400 &profile=excel&filter=AGEGROUP:YEARS05-14;AGEGROUP:YEARS15- 29;AGEGROUP:YEARS30-49;AGEGROUP:YEARS50-69;AGEGROUP:YEARS70 ;MGHEREG:REG6_AFR;GHECAUSES:*;SEX:*

Hot dogs story. (2013, November 16). Retrieved from lib.stat.cmu.edu/DASL/Stories/Hotdogs.html

Leprosy: Number of reported cases by country. (2013, September 04). Retrieved from http://apps.who.int/gho/data/node.main.A1639

Magazine ads readability. (2013, December 04). Retrieved from lib.stat.cmu.edu/DASL/Datafiles/magadsdat.html

Popular kids datafile. (2013, December 05). Retrieved from lib.stat.cmu.edu/DASL/Datafil...pularKids.html

Schultz, S. T., Klonoff-Cohen, H. S., Wingard, D. L., Askhoomoff, N. A., Macera, C. A., Ji, M., & Bacher, C. (2006). Breastfeeding, infant formula supplementation, and autistic disorder: the results of a parent survey. International Breastfeeding Journal, 1(16), doi: 10.1186/1746-4358-1-16

Waste run up. (2013, December 04). Retrieved from lib.stat.cmu.edu/DASL/Stories/wasterunup.html