3.6: Conditional Probability
- Page ID
- 36658
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Find conditional probabilities
- Use the General Multiplication Rule for probabilities of dependent events
The probability of event B happening, given that event A already happened, is called the conditional probability. The conditional probability of B, given A is written as \(P(B | A)\), and is read as “the probability of B given A happened first.” We can use the General Multiplication Rule when two events are dependent.
General Multiplication Rule: \(P(A \cap B) = P(A) \cdot P(B | A) \)
A bag contains 10 colored marbles: 7 red and 3 blue. A random experiment consists of drawing a marble from the bag, then drawing another marble without replacement (without putting the first marble back in the bag). Find the probability of drawing a red marble on the first draw (event R1), and drawing another red marble on the second draw (event R2).
Solution
Drawing a red marble on the first draw and drawing a red marble on the second draw are dependent events because we do not place the marble back in the bag. The probability of drawing a red marble on the first draw is P(R1) = \(\dfrac{7}{10}\), but on the second draw, the probability of drawing a red marble given that a red marble was drawn on the first draw is P(R2|R1) = \(\dfrac{6}{9}\).
Thus, by the General Multiplication Rule, P(R1 and R2) = P(R1)·P(R2|R1) = \(\dfrac{7}{10} \cdot \dfrac{6}{9}\) = 0.4667.
A bag contains 10 colored marbles: 7 red and 3 blue. A random experiment consists of drawing a marble from the bag, then drawing another marble without replacement. Create the tree diagram for this experiment and compute the probabilities of each outcome.
Solution
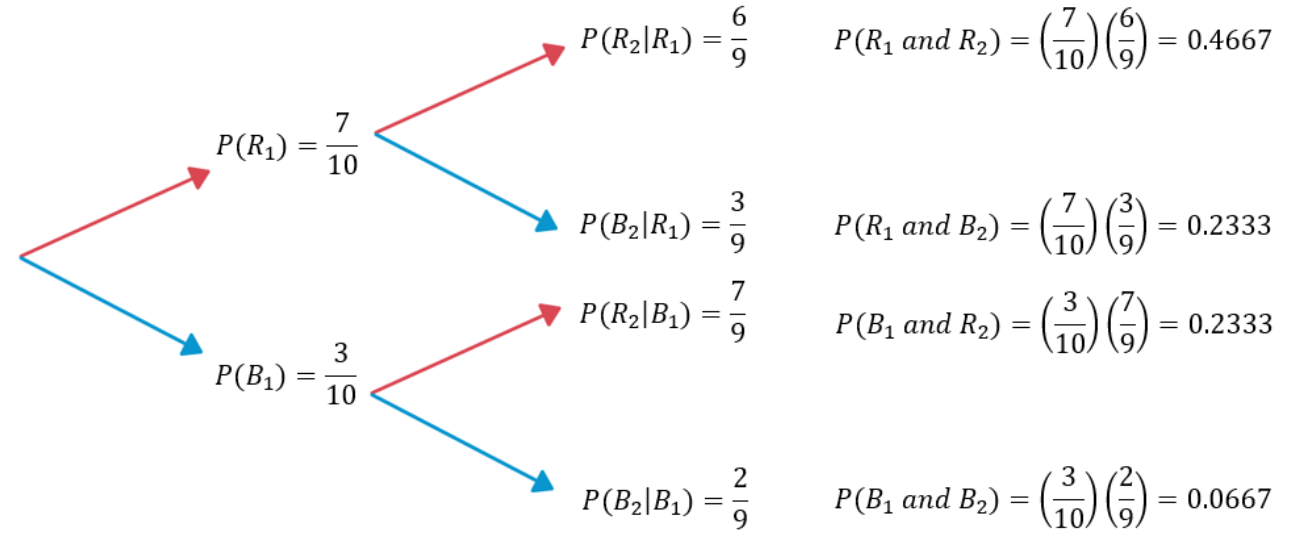
Figure \(\PageIndex{1}\)
If we multiply the probabilities as we move from left to right on each set of tree branches as shown in Figure \(\PageIndex{1}\), we get the intersections. For example, by the General Multiplication Rule, P(R1 and R2) = P(R1)·P(R2|R1) = \(\dfrac{7}{10} \cdot \dfrac{6}{9}\) = 0.4667.
Put the four intersection values into a contingency table and total the rows and columns. The table will help solve probability questions of other events.
| R2 | B2 | Total | |
|---|---|---|---|
| R1 | 0.4667 | 0.2333 | 0.7 |
| B1 | 0.2333 | 0.0667 | 0.3 |
| Total | 0.7 | 0.3 | 1 |
The grand total should add up to 1 since it represents 100% of the sample space.
Conditional Probability Rule: \(P (A |B ) = \dfrac{P(A \cap B)}{P(B)}\) or \(P (B |A ) = \dfrac{P(A \cap B)}{P(A)}\)
The following table shows the relative frequency of utility contracts granted for a specific year. One contractor is randomly chosen.
| Corporation | Government | Individual | Total | |
|---|---|---|---|---|
| United States | 0.45 | 0.007 | 0.08 | 0.537 |
| Foreign | 0.41 | 0.003 | 0.05 | 0.463 |
| Total | 0.86 | 0.01 | 0.13 | 1 |
- Find the probability the contractor is from the United States and is a corporation.
- Find the probability the contractor is from the United States given that they are a corporation.
- If the contractor is from a foreign country, what is the probability that it is from a government?
- Are the events a “contractor is an individual” and “contractor from the United States” independent?
Solution
- For the intersection in the contingency tables, find where the row and column meet. Thus, P(U.S. \(\cap\) Corporation) = 0.45.
- P (U.S.|Corporation) = \(\dfrac{P(\text { U.S.} \cap \text{Corporation})}{P(\text {Corporation})}\) = \(\dfrac{0.45}{0.86}\) = 0.5233.
- P (Government|Foreign) = \(\dfrac{P(\text { Government} \cap \text{ Foreign})}{P(\text {Foreign})}\) = \(\dfrac{0.003}{0.463}\) = 0.0065.
- Do not assume independence between two variables in a contingency table since the data may show relationships that you didn’t know were there. Use the Multiplication Rule for independent events to determine if they are independent. If the two events are independent then we would have P(Individual \(\cap\) U.S.) = P(Individual) \(\cdot\) P(U.S.). First, find the intersection using where the row and column meet to get P(Individual \(\cap\) U.S.) = 0.08. Then, use the row and column totals to find P(Individual) \(\cdot\) P(U.S.) = (0.13)(0.537) = 0.0698. Since P(Individual \(\cap\) U.S.) ≠ P(Individual) \(\cdot\) P(U.S.), these two events are dependent.
A random sample of 500 people was taken from the 2020 United States Census. Their marital status and race were recorded in the following contingency table. A person is randomly chosen. Find the following probabilities.
| Marital Status/Race | American Indian | Black | Asian | White | 2 Major Races | Total |
|---|---|---|---|---|---|---|
| Divorced | 0 | 6 | 1 | 30 | 1 | 38 |
| Married | 1 | 25 | 23 | 156 | 4 | 209 |
| Single | 2 | 33 | 21 | 155 | 11 | 222 |
| Widowed | 0 | 7 | 2 | 22 | 0 | 31 |
| Total | 3 | 71 | 47 | 363 | 16 | 500 |
- P(Single and Asian)
- P(Single | Asian)
- Given that a person is single, what is the probability their race is Asian?
Solution
- The intersection for a contingency table is where the row and column meet. There are 21 single Asians, therefore the P(Single \(\cap\) Asian) = P(Single and Asian) = \(\dfrac{21}{500}\) = 0.042. Do not multiply the row total times the column total since there is no indication that these are independent events.
- In words, we are trying to find the probability that the person is single given that we already know that their race is Asian. Using the Conditional Probability Rule, we get P(Single | Asian) = \(\dfrac{P(\text { Single} \cap \text{Asian})}{P(\text {Asian})}\) = \(\dfrac{\frac{21}{500}}{\frac{47}{500}} = \dfrac{21}{47}\) = 0.4468.
- This seems similar to the last question, however this time we are given that the person is single. We want to find P(Asian | Single) = \(\dfrac{P(\text { Asian} \cap \text{Single})}{P(\text {Single})}\)= \(\dfrac{\frac{21}{500}}{\frac{222}{500}} = \dfrac{21}{222}\) = 0.0946.
Keep in mind that P(A | B) ≠ P(B | A) since we would divide by a different total in the equation.
A blood test correctly detects a certain disease 95% of the time (positive result), and correctly detects no disease present 90% of the time (negative result). It is estimated that 25% of the population have the disease. A person takes the blood test and they get a positive result. What is the probability that they have the disease?
Solution
Let D = Having the Disease, D' = Not having the disease, + is a positive result, and – is a negative result. We are given the following in the problem: P(+ | D) = 0.95, P(– | D' ) = 0.90, P(D) = 0.25. We want to find P (D |+) = \(\dfrac{P(D \cap+)}{P(+)}\). Construct a tree diagram of outcomes.
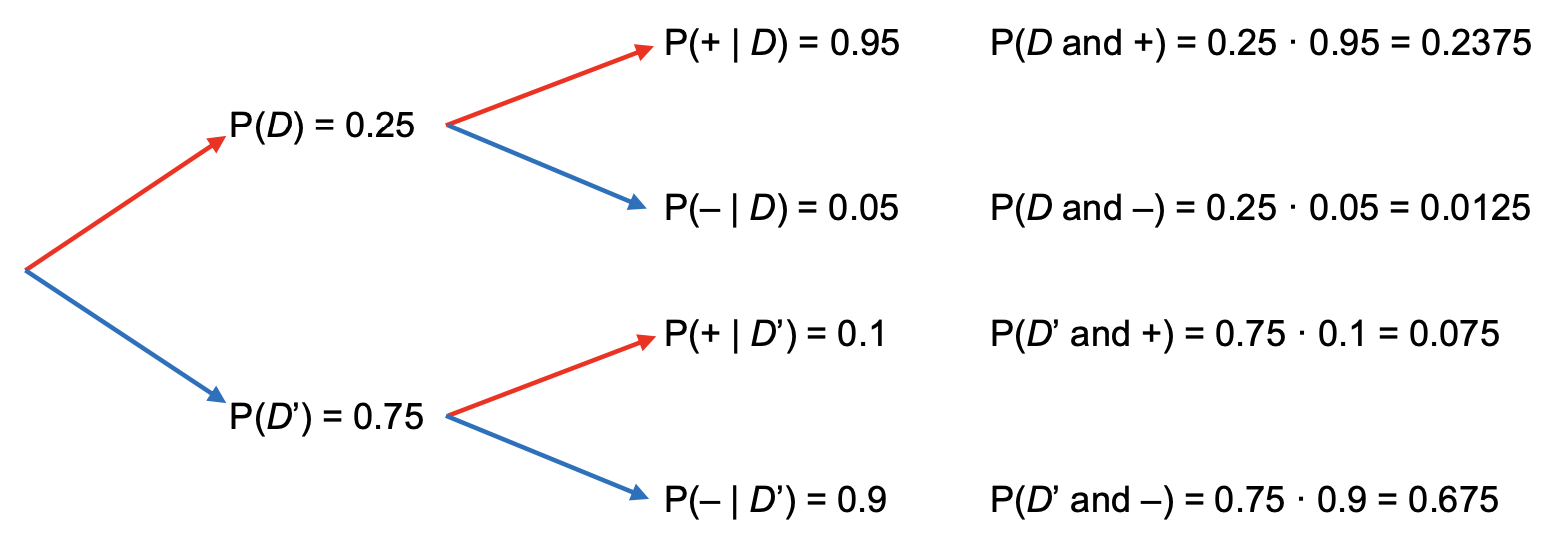
Figure \(\PageIndex{2}\)
When you multiply each pair of tree branches from left to right as shown in Figure \(\PageIndex{2}\), you are finding the intersection of the events. Place the multiplied values in a table. Note that the 0.2375 is not our answer. This is the probability of the people who have the disease and tested positive, but does not take into consideration the false positives. Since we know that the result was positive, we only divide by the proportion of positive results.
| D' | D | Total | |
|---|---|---|---|
| + | 0.075 | 0.2375 | 0.3125 |
| – | 0.675 | 0.0125 | 0.6875 |
| Total | 0.75 | 0.25 | 1 |
\(P (D|+) = \dfrac{P(D \cap +)}{P(+)} = \dfrac{0.2375}{0.3125} = 0.76\)
There is a 76% chance that they have the disease given that they tested positive. Using a table makes the probabilities easier to find. Note also that this blood test has a probability of 0.075 or 7.5% chance that a person tests positive but does not actually have the disease (false positive) and a probability of 0.0125 or 1.25% chance that a person tests negative but actually has the disease (false negative).


