10.2.2.1: Multiplying Fractions and Mixed Numbers
- Page ID
- 30879
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Multiply two or more fractions.
- Multiply a fraction by a whole number.
- Multiply two or more mixed numbers.
- Solve application problems that require multiplication of fractions or mixed numbers.
Introduction
Just as you add, subtract, multiply, and divide when working with whole numbers, you also use these operations when working with fractions. There are many times when it is necessary to multiply fractions and mixed numbers. For example, this recipe will make 4 crumb piecrusts:
5 cups graham crackers
8 tablespoons sugar
\(\ 1 \frac{1}{2}\) cups melted butter
\(\ \frac{1}{4}\) teaspoon vanilla
Suppose you only want to make 2 crumb piecrusts. You can multiply all the ingredients by \(\ \frac{1}{2}\), since only half of the number of piecrusts are needed. After learning how to multiply a fraction by another fraction, a whole number or a mixed number, you should be able to calculate the ingredients needed for 2 piecrusts.
Multiplying Fractions
When you multiply a fraction by a fraction, you are finding a “fraction of a fraction.” Suppose you have \(\ \frac{3}{4}\) of a candy bar and you want to find \(\ \frac{1}{2}\) of the \(\ \frac{3}{4}\):
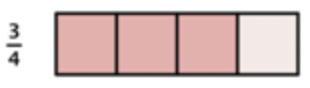
By dividing each fourth in half, you can divide the candy bar into eighths.
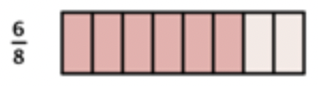
Then, choose half of those to get \(\ \frac{3}{8}\).
In both of the above cases, to find the answer, you can multiply the numerators together and the denominators together.
\(\ \frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}=\frac{\text { product of the numerators }}{\text { product of the denominators }}\)
Example:
\(\ \frac{3}{4} \cdot \frac{1}{2}=\frac{3 \cdot 1}{4 \cdot 2}=\frac{3}{8}\)
\(\ \frac{a}{b} \cdot \frac{c}{d} \cdot \frac{e}{f}=\frac{a \cdot c \cdot e}{b \cdot d \cdot f}\)
Example:
\(\ \frac{1}{3} \cdot \frac{2}{4} \cdot \frac{3}{5}=\frac{1 \cdot 2 \cdot 3}{3 \cdot 4 \cdot 5}=\frac{6}{60}\)
| \(\ \frac{2}{3} \cdot \frac{4}{5}\) | Multiply. |
Solution
| \(\ \frac{2 \cdot 4}{3 \cdot 5}\) | Multiply the numerators and multiply the denominators. |
| \(\ \frac{8}{15}\) | Simplify, if possible. This fraction is already in lowest terms. |
\(\ \frac{8}{15}\)
If the resulting product needs to be simplified to lowest terms, divide the numerator and denominator by common factors.
| \(\ \frac{2}{3} \cdot \frac{1}{4}\) | Multiply. Simplify the answer. |
Solution
| \(\ \frac{2 \cdot 1}{3 \cdot 4}\) | Multiply the numerators and multiply the denominators. |
| \(\ \frac{2}{12}\) | Simplify, if possible. |
| \(\ \frac{2 \div 2}{12 \div 2}\) | Simplify by dividing the numerator and denominator by the common factor 2. |
\(\ \frac{2}{3} \cdot \frac{1}{4}=\frac{1}{6}\)
You can also simplify the problem before multiplying, by dividing common factors.
| \(\ \frac{2}{3} \cdot \frac{1}{4}\) | Multiply. Simplify the answer. |
Solution
| \(\ \frac{2 \cdot 1}{3 \cdot 4}=\frac{1 \cdot 2}{3 \cdot 4}\) | Reorder the numerators so that you can see a fraction that has a common factor. |
| \(\ \frac{1 \cdot 1}{3 \cdot 2}\) |
Simplify. \(\ \frac{2}{4}=\frac{2 \div 2}{4 \div 2}=\frac{1}{2}\) |
\(\ \frac{2}{3} \cdot \frac{1}{4}=\frac{1}{6}\)
You do not have to use the “simplify first” shortcut, but it could make your work easier because it keeps the numbers in the numerator and denominator smaller while you are working with them.
\(\ \frac{3}{4} \cdot \frac{1}{3}\) Multiply. Simplify the answer.
- \(\ \frac{3}{12}\)
- \(\ \frac{4}{7}\)
- \(\ \frac{1}{4}\)
- \(\ \frac{36}{144}\)
- Answer
-
- Incorrect. \(\ \frac{3}{12}\) is an equivalent fraction to the correct answer \(\ \frac{1}{4}\), but it is not in lowest terms. You must divide numerator and denominator by the common factor 3. The correct answer is \(\ \frac{1}{4}\).
- Incorrect. You may have added numerators (3+1) and added denominators (4+3) instead of multiplying. The correct answer is \(\ \frac{1}{4}\).
- Correct. One way to find this answer is to multiply numerators and denominators, \(\ \frac{3 \cdot 1}{4 \cdot 3}=\frac{3}{12}\), then simplify: \(\ \frac{3 \div 3}{12 \div 3}=\frac{1}{4}\).
- Incorrect. You probably found a common denominator, multiplied correctly, but then forgot to simplify. Finding a common denominator is not necessary and makes the multiplication harder because you are working with greater than necessary numbers. The correct answer is \(\ \frac{1}{4}\).
Multiplying a Fraction by a Whole Number
When working with both fractions and whole numbers, it is useful to write the whole number as an improper fraction (a fraction where the numerator is greater than or equal to the denominator). All whole numbers can be written with a "1" in the denominator. For example: \(\ 2=\frac{2}{1}\), \(\ 5=\frac{5}{1}\), and \(\ 100=\frac{100}{1}\). Remember that the denominator tells how many parts there are in one whole, and the numerator tells how many parts you have.
\(\ a \cdot \frac{b}{c}=\frac{a}{1} \cdot \frac{b}{c}\)
Example:
\(\ 4 \cdot \frac{2}{3}=\frac{4}{1} \cdot \frac{2}{3}=\frac{8}{3}\)
Often when multiplying a whole number and a fraction, the resulting product will be an improper fraction. It is often desirable to write improper fractions as a mixed number for the final answer. You can simplify the fraction before or after rewriting it as a mixed number. See the examples below.
| \(\ 7 \cdot \frac{3}{5}\) | Multiply. Simplify the answer and write as a mixed number. |
Solution
| \(\ \frac{7}{1} \cdot \frac{3}{5}\) | Rewrite 7 as the improper fraction \(\ \frac{7}{1}\). |
| \(\ \frac{7 \cdot 3}{1 \cdot 5}=\frac{21}{5}\) | Multiply the numerators and multiply the denominators. |
| \(\ 4 \frac{1}{5}\) | Rewrite as a mixed number. \(\ 21 \div 5=4\) with a remainder of 1. |
\(\ 7 \cdot \frac{3}{5}=4 \frac{1}{5}\)
| \(\ 4 \cdot \frac{3}{4}\) | Multiply. Simplify the answer and write as a mixed number. |
Solution
| \(\ \frac{4}{1} \cdot \frac{3}{4}\) | Rewrite 4 as the improper fraction \(\ \frac{4}{1}\). |
| \(\ \frac{4 \cdot 3}{1 \cdot 4}\) | Multiply the numerators and multiply the denominators. |
| \(\ \frac{12}{4}=3\) | Simplify. |
\(\ 4 \cdot \frac{3}{4}=3\)
\(\ 3 \cdot \frac{5}{6}\) Multiply. Simplify the answer and write it as a mixed number.
- \(\ 1 \frac{1}{7}\)
- \(\ 2 \frac{1}{2}\)
- \(\ \frac{5}{2}\)
- \(\ \frac{8}{6}\)
- Answer
-
- Incorrect. You may have added the numerators and added the denominators to get \(\ \frac{8}{7}\), which is the mixed number \(\ 1 \frac{1}{7}\). Make sure you multiply numerators and multiply denominators. Multiplying the two numbers gives you \(\ \frac{15}{6}\), and since \(\ 15 \div 6=2 \mathrm{R} 3\), the mixed number is \(\ 2 \frac{3}{6}\). The fractional part simplifies to \(\ \frac{1}{2}\). The correct answer is \(\ 2 \frac{1}{2}\).
- Correct. Multiplying the two numbers gives \(\ \frac{15}{6}\), and since \(\ 15 \div 6=2 \mathrm{R} 3\), the mixed number is \(\ 2 \frac{3}{6}\). The fractional part simplifies to \(\ \frac{1}{2}\).
- Incorrect. Multiplying the numerators and multiplying the denominators results in the improper fraction \(\ \frac{5}{2}\), but you need to express this as a mixed number. The correct answer is \(\ 2 \frac{1}{2}\).
- Incorrect. You may have added numerators and placed it over the denominator of 6. Make sure you multiply numerators and multiply denominators. Multiplying the two numbers gives \(\ \frac{15}{6}\), and since \(\ 15 \div 6=2 \mathrm{R} 3\), the mixed number is \(\ 2 \frac{3}{6}\). The fractional part simplifies to \(\ \frac{1}{2}\). The correct answer is \(\ 2 \frac{1}{2}\).
Multiplying Mixed Numbers
If you want to multiply two mixed numbers, or a fraction and a mixed number, you can again rewrite any mixed number as an improper fraction.
So, to multiply two mixed numbers, rewrite each as an improper fraction and then multiply as usual. Multiply numerators and multiply denominators and simplify. And, as before, when simplifying, if the answer comes out as an improper fraction, then convert the answer to a mixed number.
| \(\ 2 \frac{1}{5} \cdot 4 \frac{1}{2}\) | Multiply. Simplify the answer and write as a mixed number. |
Solution
| \(\ 2 \frac{1}{5}=\frac{11}{5}\) | Change 2 \(\ \frac{1}{5}\) to an improper fraction. \(\ 5 \cdot 2+1=11\), and the denominator is 5. |
| \(\ 4 \frac{1}{2}=\frac{9}{2}\) | Change \(\ 4 \frac{1}{2}\) to an improper fraction. \(\ 2 \cdot 4+1=9\), and the denominator is 2. |
| \(\ \frac{11}{5} \cdot \frac{9}{2}\) | Rewrite the multiplication problem, using the improper fractions. |
| \(\ \frac{11 \cdot 9}{5 \cdot 2}=\frac{99}{10}\) | Multiply numerators and multiply denominators. |
| \(\ \frac{99}{10}=9 \frac{9}{10}\) | Write as a mixed number. \(\ 99 \div 10=9\) with a remainder of 9. |
\(\ 2 \frac{1}{5} \cdot 4 \frac{1}{2}=9 \frac{9}{10}\)
| \(\ \frac{1}{2} \cdot 3 \frac{1}{3}\) | Multiply. Simplify the answer and write as a mixed number. |
Solution
| \(\ 3 \frac{1}{3}=\frac{10}{3}\) | Change \(\ 3 \frac{1}{3}\) to an improper fraction. \(\ 3 \cdot 3+1=10\), and the denominator is 3. |
| \(\ \frac{1}{2} \cdot \frac{10}{3}\) | Rewrite the multiplication problem, using the improper fraction in place of the mixed number. |
| \(\ \frac{1 \cdot 10}{2 \cdot 3}=\frac{10}{6}\) | Multiply numerators and multiply denominators. |
| \(\ \frac{10}{6}=1 \frac{4}{6}\) | Rewrite as a mixed number. \(\ 10 \div 6=1\) with a remainder of 4. |
| \(\ 1 \frac{2}{3}\) | Simplify the fractional part to lowest terms by dividing the numerator and denominator by the common factor 2. |
\(\ \frac{1}{2} \cdot 3 \frac{1}{3}=1 \frac{2}{3}\)
As you saw earlier, sometimes it’s helpful to look for common factors in the numerator and denominator before you simplify the products.
| \(\ 1 \frac{3}{5} \cdot 2 \frac{1}{4}\) | Multiply. Simplify the answer and write as a mixed number. |
Solution
| \(\ 1 \frac{3}{5}=\frac{8}{5}\) | Change \(\ 1 \frac{3}{5}\) to an improper fraction. \(\ 5 \cdot 1+3=8\), and the denominator is 5. |
| \(\ 2 \frac{1}{4}=\frac{9}{4}\) | Change \(\ 2 \frac{1}{4}\) to an improper fraction. \(\ 4 \cdot 2+1=9\), and the denominator is 4. |
| \(\ \frac{8}{5} \cdot \frac{9}{4}\) | Rewrite the multiplication problem using the improper fractions. |
| \(\ \frac{8 \cdot 9}{5 \cdot 4}=\frac{9 \cdot 8}{5 \cdot 4}\) | Reorder the numerators so that you can see a fraction that has a common factor. |
| \(\ \frac{9 \cdot 8}{5 \cdot 4}=\frac{9 \cdot 2}{5 \cdot 1}\) | Simplify. \(\ \frac{8}{4}=\frac{8 \div 4}{4 \div 4}=\frac{2}{1}\) |
| \(\ \frac{18}{5}\) | Multiply. |
| \(\ \frac{18}{5}=3 \frac{3}{5}\) | Write as a mixed fraction. |
\(\ 1 \frac{3}{5} \cdot 2 \frac{1}{4}=3 \frac{3}{5}\)
In the last example, the same answer would be found if you multiplied numerators and multiplied denominators without removing the common factor. However, you would get \(\ \frac{72}{20}\), and then you would need to simplify more to get your final answer.
\(\ 1 \frac{3}{5} \cdot 3 \frac{1}{3}\)
- \(\ \frac{80}{15}\)
- \(\ 5 \frac{5}{15}\)
- \(\ 4 \frac{14}{15}\)
- \(\ 5 \frac{1}{3}\)
- Answer
-
- Incorrect. You probably wrote both mixed numbers as improper fractions correctly. You probably also correctly multiplied numerators and denominators. However, this improper fraction still needs to be rewritten as a mixed number and simplified. Dividing \(\ 80 \div 15=5\) with a remainder of 5 or \(\ 5 \frac{5}{15}\), then simplifying the fractional part, the correct answer is \(\ 5 \frac{1}{3}\).
- Incorrect. You probably wrote both mixed numbers as improper fractions correctly. You probably also correctly multiplied numerators and denominators, and wrote the answer as a mixed number. However, the mixed number is not in lowest terms. \(\ \frac{5}{15}\) can be simplified to \(\ \frac{1}{3}\) by dividing numerator and denominator by the common factor 5. The correct answer is \(\ 5 \frac{1}{3}\).
- Incorrect. This is the result of adding the two numbers. To multiply, rewrite each mixed number as an improper fraction: \(\ 1 \frac{3}{5}=\frac{8}{5}\) and \(\ 3 \frac{1}{3}=\frac{10}{3}\). Next, multiply numerators and multiply denominators: \(\ \frac{8}{5} \cdot \frac{10}{3}=\frac{80}{15}\). Then, write the resulting improper fraction as a mixed number: \(\ \frac{80}{15}=5 \frac{5}{15}\). Finally, simplify the fractional part by dividing both numerator and denominator by the common factor, 5. The correct answer is \(\ 5 \frac{1}{3}\).
- Correct. First, rewrite each mixed number as an improper fraction: \(\ 1 \frac{3}{5}=\frac{8}{5}\) and \(\ 3 \frac{1}{3}=\frac{10}{3}\). Next, multiply numerators and multiply denominators: \(\ \frac{8}{5} \cdot \frac{10}{3}=\frac{80}{15}\). Then write as a mixed fraction \(\ \frac{80}{15}=5 \frac{5}{15}\). Finally, simplify the fractional part by dividing both numerator and denominator by the common factor 5.
Solving Problems by Multiplying Fractions and Mixed Numbers
Now that you know how to multiply a fraction by another fraction, by a whole number, or by a mixed number, you can use this knowledge to solve problems that involve multiplication and fractional amounts. For example, you can now calculate the ingredients needed for the 2 crumb piecrusts.
| 5 cups graham crackers 8 tablespoons sugar \(\ 1 \frac{1}{2}\) cups melted butter \(\ \frac{1}{4}\) teaspoon vanilla | The recipe at left makes 4 piecrusts. Find the ingredients needed to make only 2 piecrusts. |
Solution
| Since the recipe is for 4 piecrusts, you can multiply each of the ingredients by \(\ \frac{1}{2}\) to find the measurements for just 2 piecrusts. | |
|
\(\ 5 \cdot \frac{1}{2}=\frac{5}{1} \cdot \frac{1}{2}=\frac{5}{2}\) \(\ 2 \frac{1}{2}\) cups of graham crackers are needed. |
5 cups graham crackers: Since the result is an improper fraction, rewrite \(\ \frac{5}{2}\) as the improper fraction \(\ 2 \frac{1}{2}\). |
|
\(\ 8 \cdot \frac{1}{2}=\frac{8}{1} \cdot \frac{1}{2}=\frac{8}{2}=4\) 4 tablespoons sugar is needed. |
8 tablespoons sugar: This is another example of a whole number multiplied by a fraction. |
|
\(\ \frac{3}{2} \cdot \frac{1}{2}=\frac{3}{4}\) \(\ \frac{3}{4}\) cup melted butter is needed. |
\(\ 1 \frac{1}{2}\) cups melted butter: You need to multiply a mixed number by a fraction. So, first rewrite \(\ 1 \frac{1}{2}\) as the improper fraction \(\ \frac{3}{2}\): \(\ 2 \cdot 1+1\), and the denominator is 2. Then, rewrite the multiplication problem, using the improper fraction in place of the mixed number. Multiply. |
|
\(\ \frac{1}{4} \cdot \frac{1}{2}=\frac{1}{8}\) \(\ \frac{1}{8}\) teaspoon vanilla is needed. |
\(\ \frac{1}{4}\) teaspoon vanilla: Here, you multiply a fraction by a fraction. |
The ingredients needed for 2 pie crusts are:
\(\ 2 \frac{1}{2}\) cups graham crackers
4 tablespoons sugar
\(\ \frac{3}{4}\) cup melted butter
\(\ \frac{1}{8}\) teaspoon vanilla
Often, a problem indicates that multiplication by a fraction is needed by using phrases like “half of,” “a third of,” or "\(\ \frac{3}{4}\) of."
The cost of a vacation is \(\ \$ 4,500\) and you are required to pay \(\ \frac{1}{5}\) of that amount when you reserve the trip. How much will you have to pay when you reserve the trip?
Solution
| \(\ 4,500 \cdot \frac{1}{5}\) | You need to find \(\ \frac{1}{5}\) of 4,500. “Of” tells you to multiply. |
| \(\ \frac{4,500}{1} \cdot \frac{1}{5}\) | Change 4,500 to an improper fraction by rewriting it with 1 as the denominator. |
| \(\ \frac{4,500}{5}\) | Divide. |
| \(\ 900\) | Simplify. |
You will need to pay \(\ \$ 900\) when you reserve the trip.
 |
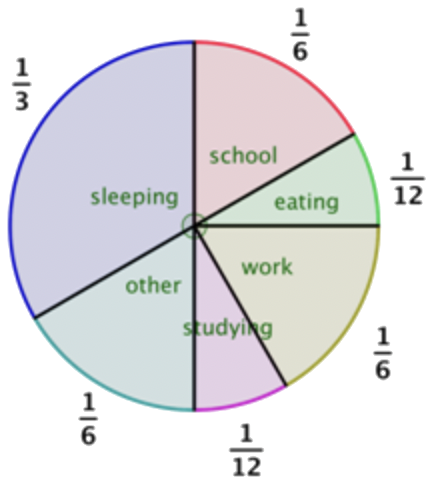The pie chart at left represents the fractional part of daily activities. Given a 24-hour day, how many hours are spent sleeping? Attending school? Eating? Use the pie chart to determine your answers. |
Solution
| \(\ \frac{1}{3} \cdot 24\) = number of hours sleeping | Sleeping is \(\ \frac{1}{3}\) of the pie, so the number of hours spent sleeping is \(\ \frac{1}{3}\) of 24. |
| \(\ \frac{1}{3} \cdot \frac{24}{1}=8\) | Rewrite 24 as an improper fraction with a denominator of 1. |
|
\(\ \frac{24}{3}=8\) 8 hours sleeping |
Multiply numerators and multiply denominators. Simplify \(\ \frac{24}{3}\) to 8. |
| \(\ \frac{1}{6} \cdot 24\) = number of hours spent at school | Attending school is \(\ \frac{1}{6}\) of the pie, so the number of hours spent attending school is \(\ \frac{1}{6}\) of 24. |
| \(\ \frac{1}{6} \cdot \frac{24}{1}\) | Rewrite 24 as an improper fraction with a denominator of 1. |
|
\(\ \frac{24}{6}=4\) 4 hours attending school |
Multiply numerators and multiply denominators. Simplify \(\ \frac{24}{6}\) to 4. |
| \(\ \frac{1}{12} \cdot 24\) = number of hours spent eating | Eating is \(\ \frac{1}{12}\) of the pie, so the number of hours spent eating is \(\ \frac{1}{12}\) of 24. |
| \(\ \frac{1}{12} \cdot \frac{24}{1}\) | Rewrite 24 as an improper fraction with a denominator of 1. |
|
\(\ \frac{24}{12}=2\) 2 hours spent eating |
Multiply numerators and multiply denominators. Simplify \(\ \frac{24}{12}\) to 2. |
Hours spent:
sleeping: 8 hours
attending school: 4 hours
eating: 2 hours
Neil bought a dozen (12) eggs. He used \(\ \frac{1}{3}\) of the eggs for breakfast. How many eggs are left?
- 8
- 4
- 9
- 3
- Answer
-
- Correct. \(\ \frac{1}{3}\) of 12 is \(\ 4\left(\frac{1}{3} \cdot \frac{12}{1}=\frac{12}{3}=4\right)\), so he used 4 of the eggs. Because \(\ 12-4=8\), there are 8 eggs left.
- Incorrect. \(\ \frac{1}{3}\) of 12 is 4, but that gives how many eggs Neil used, not how many he had left. You need to subtract 4 from 12 to find the number of remaining eggs. The correct answer is 8.
- Incorrect. You may have incorrectly found \(\ \frac{1}{3}\) of 12 to be \(\ \text { 3. } \frac{1}{3}\) of 12 is 4, and then 12-4 is 8. The correct answer is 8.
- Incorrect. You need to find \(\ \frac{1}{3}\) of 12, which is 4. Then subtract 4 from 12 to get 8 remaining eggs.
Summary
You multiply two fractions by multiplying the numerators and multiplying the denominators. Often the resulting product will not be in lowest terms, so you must also simplify. If one or both fractions are whole numbers or mixed numbers, first rewrite each as an improper fraction. Then multiply as usual, and simplify.