Ch 6.1 Standard Normal Distribution
- Page ID
- 15900
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ch 6.1 Standard Normal distribution
Normal Density Curve
A random variable X has a distribution with a graph that is symmetric and bell-shaped, and it can be described by the equation given by
\( y = \frac{e^{\frac{-1}{2}\cdot {(\frac{x-\mu}{\sigma})}^2}}{\sigma \sqrt{2 \pi}} \) , then it has a “Normal distribution”
Normal Density Curve:
Note: the distribution is determined by μ and σ.
Z-score
Z-score of x = \( \frac{x-\mu}{\sigma} \) is the standardized value of x.
z-score tells the number of standard deviation X is above or below the mean. Positive z implies X is above the mean, negative z implies X is below the mean.
A) Standard Normal
(also known as z distribution) is a normal distribution with parameters:
Mean μ = 0 and standard deviation σ = 1.
The total area under its density curve is equal to 1.
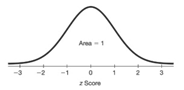
Properties of standard normal (z-normal):
- area left of z of 0 = 0.5
- area right of z of 0 = 0.5
- area left of z = area right of - z
- area right of z = 1 – area left of z
B) Empirical Rule (68-95-99.7)
If X is normally distributed, 68% are within 1 sd from the mean. 95% are within 2 sd from the mean, 99.7% are within 3 sd from the mean.
P( Z-score between -1 and 1 ) = 68%
P( Z-score between -2 and 2 ) = 95%
P( Z-score between -3 and 3 ) = 99.7%
Ex1. Weight of a certain type of dog is normally distributed with mean = 18 lb. and standard deviation of 2 lb.
write the marking of mean, mean - 1sd, mean - 2sd, mean + sd, mean + 2d on a number line.
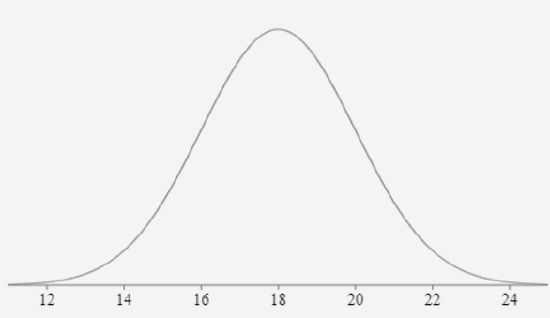
a) What is the z-score of 14lb and 22 lb? What is the probability that a dog weighs between 14 lb and 22lb?
14 and 22 are 2 sd from the mean, so according to the Empirical rule, the probability is 95%.
b) What is the z-score of 20lb and 16lb? What is the probability that a dog weighs between 16lb and 20 lb?
16 and 20 are 1 sd from the mean, so according to the Empirical rule, the probability is 68%.
c) What is the z-score of 24 lb and 12 lb? What is the probability that a dog weigh between 12 lb and 24lb?
24 is 3 sd above the mean, so z-score of 24 lb is 3.
12 is 3 sd below the mean, so z-score of 12 lb is -3.
C) Probability of z-score in standard normal
Use online Normal distribution calculator
http://onlinestatbook.com/2/calculators/normal_dist.html
Specify mean μ =0 standard deviation &sigma&
-For left area or P(x < a) click below
-For right area or P(x > a) click above
-For area between two values a and b P( a < x < b), click between
-For area outside of a and b, P(x < a or x > b), click outside
-Click “Recalculate”
Ex1: Find probability that z is between -1.8 and 1.8. Sketch the area.
Use online Normal calculator Mean = 0, SD = 1
Click between, enter -1.8, 1.8
Recalculate: P( -1.8 < z < 1.8 ) = 0.9281
Ex2. Find the probability that z is less than 0.44. Sketch the area.
Use online Normal calculator μ =0 , SD=1
Click below , enter 0.44
Recalculate: P( z < 0.44 ) = 0.67
Ex3. Find the probability that z is greater than 1.8. Sketch the area.
Use online Normal calculator μ =0 , SD=1
Click above , enter 1.8
Recalculate: P( z >1.8) = 0.0359
Ex 4. Find the probability that z is less than – 1.2. Sketch the area.

Use online Normal calculator μ =0 , SD=1
Click below , enter -1.2
Recalculate: P( z < -1.2) = 0.1151
D) Find percentile of a z-score
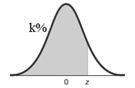 k Percentile corresponds to a value that is higher thank% of all values. Or k% of data are less than the k percentile value. This corresponds to left area of k%.
k Percentile corresponds to a value that is higher thank% of all values. Or k% of data are less than the k percentile value. This corresponds to left area of k%.
Ex5. What percentile is the z-score 2.2?

Use online Normal calculator Mean =0 , SD=1
Percentile is referring to 2.2 or less. Click below , enter 2.2
Recalculate: P( z < 2.2) = 0.9861 = 98.6%
Round to whole percent = 99th percentile
Ex 6. What percentile is the z-score -1.35

Use online Normal calculator μ =0 , σ=1
Click below , enter -1.35
Recalculate: P( z < -1.35) = 0.0885 = 8.9%
Round to whole percent. 9th percentile
E) Find z-score given area or percentile.
Online Inverse Normal calculator is use to find the z-score that is the cut-off for the left area, right area or percentile.
http://onlinestatbook.com/2/calculators/inverse_normal_dist.html
Specify area, mean= 0 and SD= 1
Select if area is below, above, between or outside.
Click “Recalculate”
Ex1. Find the z-score that corresponds to bottom 10% of all values.
Use Inverse Normal Calculator. Convert 10% to 0.1.
Specify area = 0.1, Mean = 0, sd =1,
Click below.
Recalculate. P( z < __-1.28_____ ) = 0.1, cut-off z = -1.28
Ex2. Find the cutoff for top 20%.
 Use Inverse Normal Calculator. Convert 20% to 0.2.
Use Inverse Normal Calculator. Convert 20% to 0.2.
Specify area = 0.2
Mean = 0, sd =1,
Click above ( for top percent). Recalculate.
P( z > __0.842______) = 0.2 z-cutoff = 0.84
Ex3. Find P91 , 91th percentile of all z.

Use Inverse Normal calculator.
Specify area = 0.91
Mean = 0, sd =1,
Click below. Recalculate.
P( z < __1.341______) = 0.91 91th percentile of all z = 1.34.
Ex4. Find P15, 15th percentile of all z.
Convert 15% = 0.15. Use Inverse Normal calculator.

Specify area = 0.15, Mean = 0, sd =1,
Click below. Recalculate
P( z < _-1.036_______) = 0.15 15th percentile = -1.04
F) Find Critical value Zα
α = significant level. The probability of unlikely, default is 0.05 if not specify.
Critical value zα : the positive z-value that separates significantly high values of z with non-significant z.
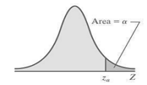 Note: Significantly low critical value = - zα
Note: Significantly low critical value = - zα
To find zα: Use Inverse Normal calculator
Specify area = α, Mean = 0, sd =1,
Click above. Recalculate.
Ex1. Given α = 0.02, Find the critical value Z0.02.

Use Inverse Normal calculator
Specify area = 0.02, Mean = 0, sd =1,
Click above. Recalculate.
Z0.02 = 2.054
Ex2. Given α = 0.06, find the critical value Z0.06

Use Inverse Normal calculator
Specify area = 0.06, Mean = 0, sd =1,
Click above. Recalculate.
Z0.06 = 1.555

