Ch 4.1 Discrete Random Variable
- Page ID
- 15873
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ch 4.1 Discrete Random Variable
Random Variable
Random Variable: is a variable (X) that has a single numerical value, determined by chance, for each outcome of a procedure.
Probability distribution: is a table, formula or graph that gives the probability of each value of the random variable.
A Discrete Random Variable has a collection of values that is finite or countable similar to discrete data.
A Continuous Random Variable as infinitely many values and the collection of values is not countable.
Ex : X = the number of times “four” shows up after tossing a die 10 times is a discrete random variable.
X = weight of a student randomly selected from a class. X is a continuous random variable
X = the method a friend contacts you online. X is not a random variable. ( X is not numerical)
A Probability Distribution (PDF) for a Discrete Random Variable is a table, graph or formula that gives Probability of each value of X.
A Probability Distribution Function (PDF or PD) satisfies the following requirements:
1. The value X is numerical, not categorical and each P(x) is associated with the corresponding probability.
2 ΣP(X) = 1 . A ΣP(X) = 0.999 or 1.01 is acceptable as a result of rounding.
3. 0 ≤P(x) ≤ 1 for all P(x) in the PDF.
Ex1: PDF for number of heads in a two-coin toss are given as a table and a graph.
Table graph
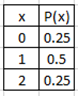
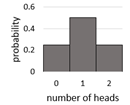
Both are valid PDF because Σ P(X) = 1
and each value of P(X) is between 0 and 1.
Ex2: The number of medical tests a patient receives after entering a hospital is given by the PDF below
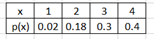
a) Is the table a valid PDF?
The table is not a probability distribution because Σ P(x) = 0.02+0.18+0.3+0.4 = 0.9 is not 1
b) Define the random variable x.
x = no. of medical tests a patient receives after entering a hospital.
c) Explain why the x = 0 is not in the PDF?
A patient always receives at least one medical test in the hospital.
Parameters of a Probability distribution:
Mean μ for a probability distribution:
\( E(x) = \mu = \sum{x\cdot P(x)} \)
Variance σ2 for a probability distribution:
\( \sigma^2 = \sum{(x-\mu)^2}\cdot P(x) \)
Standard deviation for a probability distribution:
\( \sigma = \sqrt{\sum{(x-\mu)^2}\cdot P(x)} \)
To calculate Mean, variance and standard deviation of a probability distribution by technology:
Use Libretext statistics calculator:
Enter Number of outcomes, each X and P(X), calculate.
round off rule: one more decimal place than for E(x)
Two decimal places for σ and σ2.
Expected value = the long-term outcome of average of x when the procedure is repeated infinitely many times. Round to one decimal place.
Non-significant values of X.
1. The range of X from \( \mu - 2\cdot\sigma \text{ to }\mu +2\cdot\sigma \) are non-significant. (Range of rule of Thumb)
2. X that are outside of \( \mu - 2\cdot\sigma \text{ to } \mu +2\cdot\sigma \) are significant that is unlikely to occur.
Ex1: X = no. of year a new hire will stay with the company. P(x) = Prob. that a new hire with stay for x year.
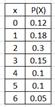 a) Find mean, variance, st. deviation and determine the Expected number of years a new hire will stay.
a) Find mean, variance, st. deviation and determine the Expected number of years a new hire will stay.
Use easycalculation.com statistics discrete random variable calculator,
Enter number of outcomes = 7. Mean = 2.4, σ2 = 2.73, σ =1.65
The Expected no. of year a new hire will stay is 2.4 years.
b) Find probability that a new hire will stay for 4 years or more.
Add P(4), P(5) and P(6) = P( 4 or more) = 0.1 + 0.1 + 0.05 = 0.25
c) Find probability that a new hire will stay for between 3 or 5 years inclusive.
P( 3 to 5 inclusive) = 0.15 + 0.1+0.1 = 0.35
d) Find the probability that a new hire will stay for 2 years or fewer.
P(2 or fewer) = 0.12 + 0.18 + 0.30 = 0.6
e) Find the range of non-significant year of stay.
2.4 -2(1.65) to 2.4 + 2(1.65) is -0.9 to 5.7
Ex2: Given x = of number of textbooks a student buy per semester. What is the expected number of textbooks?
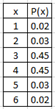 a) Find mean, variance and standard deviation.
a) Find mean, variance and standard deviation.
Use easycalculation.com statistics discrete random variable calculator, Enter number of outcomes = 6
E(x) = μ = 3.5, σ2 = 0.61, σ = 0.78
Expected number of textbook is 3.5 books.
b) Find Probability that a student buys at least 5 textbook.
P( at least 5) = P(5 or more) = 0.03 + 0.02 = 0.05,
c) Find probability that x is at most 2.
P(at most 2 ) = P( 2 or fewer) = 0.02 + 0.03 = 0.05
c) Find the range non-significant.
Range of non-significant is 3.5 – 2(0.78) to 2.5 + 2(0.78) is 1.94 to 5.06.

