2.6: Measures of the Center of the Data
- Last updated
- Save as PDF
- Page ID
- 15459
The "center" of a data set is also a way of describing location. The two most widely used measures of the "center" of the data are the mean (average) and the median. To calculate the mean weight of 50 people, add the 50 weights together and divide by 50. To find the median weight of the 50 people, order the data and find the number that splits the data into two equal parts. The median is generally a better measure of the center when there are extreme values or outliers because it is not affected by the precise numerical values of the outliers. The mean is the most common measure of the center.
Note
The ideal gas law is easy to remember and apply in solving problems, as long as you get the proper values aThe words “mean” and “average” are often used interchangeably. The substitution of one word for the other is common practice. The technical term is “arithmetic mean” and “average” is technically a center location. However, in practice among non-statisticians, “average" is commonly accepted for “arithmetic mean.”
When each value in the data set is not unique, the mean can be calculated by multiplying each distinct value by its frequency and then dividing the sum by the total number of data values. The letter used to represent the sample mean is an \(x\) with a bar over it (pronounced “\(x\) bar”): \(\overline{x}\).
The Greek letter \(\mu\) (pronounced "mew") represents the population mean. One of the requirements for the sample mean to be a good estimate of the population mean is for the sample taken to be truly random.
To see that both ways of calculating the mean are the same, consider the sample:
1; 1; 1; 2; 2; 3; 4; 4; 4; 4; 4
\[\bar{x} = \dfrac{1+1+1+2+2+3+4+4+4+4+4}{11} = 2.7\]
In the second calculation, the frequencies are 3, 2, 1, and 5.
You can quickly find the location of the median by using the expression
\[\dfrac{n+1}{2}\]
The letter \(n\) is the total number of data values in the sample. If \(n\) is an odd number, the median is the middle value of the ordered data (ordered smallest to largest). If \(n\) is an even number, the median is equal to the two middle values added together and divided by two after the data has been ordered. For example, if the total number of data values is 97, then
\[\dfrac{n+1}{2} = \dfrac{97+1}{2} = 49.\]
The median is the 49th value in the ordered data. If the total number of data values is 100, then
\[\dfrac{n+1}{2} = \dfrac{100+1}{2} = 50.5.\]
The median occurs midway between the 50th and 51st values. The location of the median and the value of the median are not the same. The upper case letter \(M\) is often used to represent the median. The next example illustrates the location of the median and the value of the median.
Example \(\PageIndex{1}\)
AIDS data indicating the number of months a patient with AIDS lives after taking a new antibody drug are as follows (smallest to largest):
3; 4; 8; 8; 10; 11; 12; 13; 14; 15; 15; 16; 16; 17; 17; 18; 21; 22; 22; 24; 24; 25; 26; 26; 27; 27; 29; 29; 31; 32; 33; 33; 34; 34; 35; 37; 40; 44; 44; 47
Calculate the mean and the median.
Answer
The calculation for the mean is:
\[\bar{x} = \dfrac{[3+4+(8)(2)+10+11+12+13+14+(15)(2)+(16)(2)+...+35+37+40+(44)(2)+47]}{40} = 23.6\]
To find the median, \(M\), first use the formula for the location. The location is:\[\dfrac{n+1}{2} = \dfrac{40+1}{2} = 20.5\]
Starting at the smallest value, the median is located between the 20th and 21st values (the two 24s):
3; 4; 8; 8; 10; 11; 12; 13; 14; 15; 15; 16; 16; 17; 17; 18; 21; 22; 22; 24; 24; 25; 26; 26; 27; 27; 29; 29; 31; 32; 33; 33; 34; 34; 35; 37; 40; 44; 44; 47
\[M = \dfrac{24+24}{2} = 24\]
Calculator
To find the mean and the median:
Clear list L1. Pres STAT 4:ClrList. Enter 2nd 1 for list L1. Press ENTER.
Enter data into the list editor. Press STAT 1:EDIT.
Put the data values into list L1.
Press STAT and arrow to CALC. Press 1:1-VarStats. Press 2nd 1 for L1 and then ENTER.
Press the down and up arrow keys to scroll.
\(\bar{x}\) = 23.6, M = 24
Exercise \(\PageIndex{1}\)
The following data show the number of months patients typically wait on a transplant list before getting surgery. The data are ordered from smallest to largest. Calculate the mean and median.
3; 4; 5; 7; 7; 7; 7; 8; 8; 9; 9; 10; 10; 10; 10; 10; 11; 12; 12; 13; 14; 14; 15; 15; 17; 17; 18; 19; 19; 19; 21; 21; 22; 22; 23; 24; 24; 24; 24
Answer
Mean: \(3 + 4 + 5 + 7 + 7 + 7 + 7 + 8 + 8 + 9 + 9 + 10 + 10 + 10 + 10 + 10 + 11 + 12 + 12 + 13 + 14 + 14 + 15 + 15 + 17 + 17 + 18 + 19 + 19 + 19 + 21 + 21 + 22 + 22 + 23 + 24 + 24 + 24 = 544\)
\[\dfrac{544}{39} = 13.95\]
Median: Starting at the smallest value, the median is the 20th term, which is 13.
Example \(\PageIndex{2}\)
Suppose that in a small town of 50 people, one person earns $5,000,000 per year and the other 49 each earn $30,000. Which is the better measure of the "center": the mean or the median?
Solution
\[\bar{x} = \dfrac{5,000,000+49(30,000)}{50} = 129,400\]
\(M = 30,000\)
(There are 49 people who earn $30,000 and one person who earns $5,000,000.)
The median is a better measure of the "center" than the mean because 49 of the values are 30,000 and one is 5,000,000. The 5,000,000 is an outlier. The 30,000 gives us a better sense of the middle of the data.
Exercise \(\PageIndex{2}\)
In a sample of 60 households, one house is worth $2,500,000. Half of the rest are worth $280,000, and all the others are worth $315,000. Which is the better measure of the “center”: the mean or the median?
Answer
The median is the better measure of the “center” than the mean because 59 of the values are $280,000 and one is $2,500,000. The $2,500,000 is an outlier. Either $280,000 or $315,000 gives us a better sense of the middle of the data.
Another measure of the center is the mode. The mode is the most frequent value. There can be more than one mode in a data set as long as those values have the same frequency and that frequency is the highest. A data set with two modes is called bimodal.
Example \(\PageIndex{3}\)
Statistics exam scores for 20 students are as follows:
50; 53; 59; 59; 63; 63; 72; 72; 72; 72; 72; 76; 78; 81; 83; 84; 84; 84; 90; 93
Find the mode.
Answer
The most frequent score is 72, which occurs five times. Mode = 72.
Exercise \(\PageIndex{3}\)
The number of books checked out from the library from 25 students are as follows:
0; 0; 0; 1; 2; 3; 3; 4; 4; 5; 5; 7; 7; 7; 7; 8; 8; 8; 9; 10; 10; 11; 11; 12; 12
Find the mode.
Answer
The most frequent number of books is 7, which occurs four times. Mode = 7.
Example \(\PageIndex{4}\)
Five real estate exam scores are 430, 430, 480, 480, 495. The data set is bimodal because the scores 430 and 480 each occur twice.
When is the mode the best measure of the "center"? Consider a weight loss program that advertises a mean weight loss of six pounds the first week of the program. The mode might indicate that most people lose two pounds the first week, making the program less appealing.
The mode can be calculated for qualitative data as well as for quantitative data. For example, if the data set is: red, red, red, green, green, yellow, purple, black, blue, the mode is red.
Statistical software will easily calculate the mean, the median, and the mode. Some graphing calculators can also make these calculations. In the real world, people make these calculations using software.
Exercise \(\PageIndex{4}\)
Five credit scores are 680, 680, 700, 720, 720. The data set is bimodal because the scores 680 and 720 each occur twice. Consider the annual earnings of workers at a factory. The mode is $25,000 and occurs 150 times out of 301. The median is $50,000 and the mean is $47,500. What would be the best measure of the “center”?
Answer
Because $25,000 occurs nearly half the time, the mode would be the best measure of the center because the median and mean don’t represent what most people make at the factory.
The Law of Large Numbers and the Mean
The Law of Large Numbers says that if you take samples of larger and larger size from any population, then the mean \(\bar{x}\) of the sample is very likely to get closer and closer to \(\mu\). This is discussed in more detail later in the text.
Sampling Distributions and Statistic of a Sampling Distribution
You can think of a sampling distribution as a relative frequency distribution with a great many samples. (See Sampling and Data for a review of relative frequency). Suppose thirty randomly selected students were asked the number of movies they watched the previous week. The results are in the relative frequency table shown below.
| # of movies | Relative Frequency |
|---|---|
| 0 |
\(\dfrac{5}{30}\) |
| 1 |
\(\dfrac{15}{30}\) |
| 2 |
\(\dfrac{6}{30}\) |
| 3 |
\(\dfrac{3}{30}\) |
| 4 |
\(\dfrac{1}{30}\) |
If you let the number of samples get very large (say, 300 million or more), the relative frequency table becomes a relative frequency distribution.
A statistic is a number calculated from a sample. Statistic examples include the mean, the median and the mode as well as others. The sample mean \(\bar{x}\) is an example of a statistic which estimates the population mean \(\mu\).
Calculating the Mean of Grouped Frequency Tables
When only grouped data is available, you do not know the individual data values (we only know intervals and interval frequencies); therefore, you cannot compute an exact mean for the data set. What we must do is estimate the actual mean by calculating the mean of a frequency table. A frequency table is a data representation in which grouped data is displayed along with the corresponding frequencies. To calculate the mean from a grouped frequency table we can apply the basic definition of mean:
\[mean = \dfrac{\text{data sum}}{\text{number of data values}}.\]
We simply need to modify the definition to fit within the restrictions of a frequency table.
Since we do not know the individual data values we can instead find the midpoint of each interval. The midpoint is
\[\dfrac{\text{lower boundary+upper boundary}}{2}.\]
We can now modify the mean definition to be
\[\text{Mean of Frequency Table} = \dfrac{\sum{fm}}{\sum{f}}\]
where \(f\) is the frequency of the interval and \(m \) is the midpoint of the interval.
Example \(\PageIndex{5}\)
A frequency table displaying professor Blount’s last statistic test is shown. Find the best estimate of the class mean.
| Grade Interval | Number of Students |
|---|---|
| 50–56.5 | 1 |
| 56.5–62.5 | 0 |
| 62.5–68.5 | 4 |
| 68.5–74.5 | 4 |
| 74.5–80.5 | 2 |
| 80.5–86.5 | 3 |
| 86.5–92.5 | 4 |
| 92.5–98.5 | 1 |
Solution
- Find the midpoints for all intervals
| Grade Interval | Midpoint |
|---|---|
| 50–56.5 | 53.25 |
| 56.5–62.5 | 59.5 |
| 62.5–68.5 | 65.5 |
| 68.5–74.5 | 71.5 |
| 74.5–80.5 | 77.5 |
| 80.5–86.5 | 83.5 |
| 86.5–92.5 | 89.5 |
| 92.5–98.5 | 95.5 |
- Calculate the sum of the product of each interval frequency and midpoint. \( 53.25(1) + 59.5(0) + 65.5(4 )+ 71.5(4) + 77.5(2) + 83.5(3) + 89.5(4) + 95.5(1) = 1460.25\)
- \(\mu = \dfrac{\sum{fm}}{\sum{f}} = \dfrac{1460.25}{19} = 76.86\)
Exercise \(\PageIndex{5}\)
Maris conducted a study on the effect that playing video games has on memory recall. As part of her study, she compiled the following data:
| Hours Teenagers Spend on Video Games | Number of Teenagers |
|---|---|
| 0–3.5 | 3 |
| 3.5–7.5 | 7 |
| 7.5–11.5 | 12 |
| 11.5–15.5 | 7 |
| 15.5–19.5 | 9 |
What is the best estimate for the mean number of hours spent playing video games?
Answer
Find the midpoint of each interval, multiply by the corresponding number of teenagers, add the results and then divide by the total number of teenagers
The midpoints are 1.75, 5.5, 9.5, 13.5,17.5.\[Mean = (1.75)(3) + (5.5)(7) + (9.5)(12) + (13.5)(7) + (17.5)(9) = 409.75\]
References
- Data from The World Bank, available online at http://www.worldbank.org (accessed April 3, 2013).
- “Demographics: Obesity – adult prevalence rate.” Indexmundi. Available online at http://www.indexmundi.com/g/r.aspx?t=50&v=2228&l=en (accessed April 3, 2013).
Review
The mean and the median can be calculated to help you find the "center" of a data set. The mean is the best estimate for the actual data set, but the median is the best measurement when a data set contains several outliers or extreme values. The mode will tell you the most frequently occuring datum (or data) in your data set. The mean, median, and mode are extremely helpful when you need to analyze your data, but if your data set consists of ranges which lack specific values, the mean may seem impossible to calculate. However, the mean can be approximated if you add the lower boundary with the upper boundary and divide by two to find the midpoint of each interval. Multiply each midpoint by the number of values found in the corresponding range. Divide the sum of these values by the total number of data values in the set.
Formula Review
\[\mu = \dfrac{\sum{fm}}{\sum{f}} \]
where \(f\) = interval frequencies and \(m\) = interval midpoints.
Exercise 2.6.6
Find the mean for the following frequency tables.
-
Grade Frequency 49.5–59.5 2 59.5–69.5 3 69.5–79.5 8 79.5–89.5 12 89.5–99.5 5 -
Daily Low Temperature Frequency 49.5–59.5 53 59.5–69.5 32 69.5–79.5 15 79.5–89.5 1 89.5–99.5 0 -
Points per Game Frequency 49.5–59.5 14 59.5–69.5 32 69.5–79.5 15 79.5–89.5 23 89.5–99.5 2
Exercise 2.6.7
Calculate the mean.
Answer
Mean: \(16 + 17 + 19 + 20 + 20 + 21 + 23 + 24 + 25 + 25 + 25 + 26 + 26 + 27 + 27 + 27 + 28 + 29 + 30 + 32 + 33 + 33 + 34 + 35 + 37 + 39 + 40 = 738\);
\(\dfrac{738}{27} = 27.33\)
Exercise 2.6.8
Identify the median.
Exercise 2.6.9
Identify the mode.
Answer
The most frequent lengths are 25 and 27, which occur three times. Mode = 25, 27
Use the following information to answer the next three exercises: Sixty-five randomly selected car salespersons were asked the number of cars they generally sell in one week. Fourteen people answered that they generally sell three cars; nineteen generally sell four cars; twelve generally sell five cars; nine generally sell six cars; eleven generally sell seven cars. Calculate the following:
Exercise 2.6.10
sample mean = \(\bar{x}\) = _______
Exercise 2.6.11
median = _______
Answer
4
Bringing It Together
Exercise 2.6.12
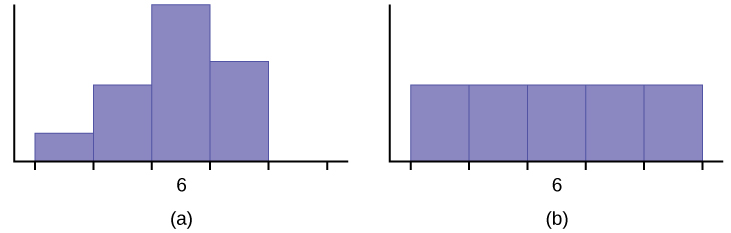
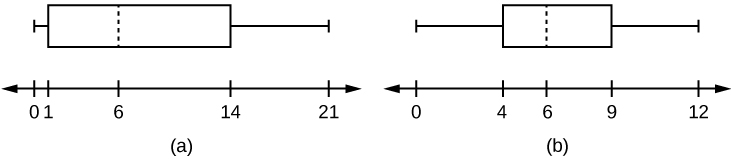
Javier and Ercilia are supervisors at a shopping mall. Each was given the task of estimating the mean distance that shoppers live from the mall. They each randomly surveyed 100 shoppers. The samples yielded the following information.
| Javier | Ercilia | |
|---|---|---|
| \(\bar{x}\) | 6.0 miles | 6.0 miles |
| s | 4.0 miles | 7.0 miles |
- How can you determine which survey was correct ?
- Explain what the difference in the results of the surveys implies about the data.
- If the two histograms depict the distribution of values for each supervisor, which one depicts Ercilia's sample? How do you know?
- If the two box plots depict the distribution of values for each supervisor, which one depicts Ercilia’s sample? How do you know?
Use the following information to answer the next three exercises: We are interested in the number of years students in a particular elementary statistics class have lived in California. The information in the following table is from the entire section.
| Number of years | Frequency | Number of years | Frequency |
|---|---|---|---|
| Total = 20 | |||
| 7 | 1 | 22 | 1 |
| 14 | 3 | 23 | 1 |
| 15 | 1 | 26 | 1 |
| 18 | 1 | 40 | 2 |
| 19 | 4 | 42 | 2 |
| 20 | 3 |
Exercise 2.6.13
What is the IQR?
- 8
- 11
- 15
- 35
Answer
a
Exercise 2.6.14
What is the mode?
- 19
- 19.5
- 14 and 20
- 22.65
Exercise 2.6.15
Is this a sample or the entire population?
- sample
- entire population
- neither
Answer
b
Glossary
- Frequency Table
- a data representation in which grouped data is displayed along with the corresponding frequencies
- Mean
- a number that measures the central tendency of the data; a common name for mean is 'average.' The term 'mean' is a shortened form of 'arithmetic mean.' By definition, the mean for a sample (denoted by \(\bar{x}\)) is \(\bar{x} = \dfrac{\text{Sum of all values in the sample}}{\text{Number of values in the sample}}\), and the mean for a population (denoted by \(\mu\)) is \(\mu = \dfrac{\text{Sum of all values in the population}}{\text{Number of values in the population}}\).
- Median
- a number that separates ordered data into halves; half the values are the same number or smaller than the median and half the values are the same number or larger than the median. The median may or may not be part of the data.
- Midpoint
- the mean of an interval in a frequency table
- Mode
- the value that appears most frequently in a set of data


