Ch 6.2 Application of Normal Distribution

Ch 6.2 Using the Normal distribution

When X is normally distributed with mean μ and standard deviation σ,  N( μ,σ) probability of  range of X can be represented by the area under normal  density curve \( y = \frac{e^{\frac{-1}{2}\cdot {(\frac{x-\mu}{\sigma})}^2}}{\sigma \sqrt{2 \pi}} \)   (no need to memorize.)

 

 

 

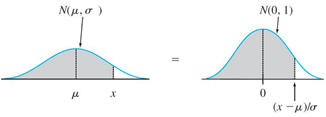
The same properties of bell shape density curve apply:

Probability = area = relative frequency (percentage)

 a) P( X > μ ) = 0.5,  P(X < μ) = 0.5

 b) P(  a < X < b) = area between a and b under the density bell curve.

A) Find Probability of X in Normal distribution

Use online Normal distribution calculator to find prob.

http://onlinestatbook.com/2/calculators/normal_dist.html

Specify mean = μ, SD= σ

-For left area or P(x < a) click below

-For right area or P(x > a) click above

-For area between two values a and b P( a < x < b), click between

-For area outside of a and b, P(x <a or x > b), click outside

-Click “Recalculate”

 

B) Find X given probability in Normal Distribution

Use Inverse Normal Calculator to find the cut-off given a left area, right area, between area or outside area of two tails.

http://onlinestatbook.com/2/calculators/inverse_normal_dist.html

Specify area, mean= μ, SD= σ

select if area is below, above, between or outside.

Click “Recalculate”

Note: left area = bottom percentage = percentile.  Right area = top percent

 a) Find cutoff X for Top k percentage:

Use Inverse online calculator, above

 b) Find cutoff X for Bottom k percentage or k percentile:  Use Inverse online calculator, below

 

Ex1. Final exam of a standardized test is normally distributed with mean 63 and standard deviation 5.

a) Find the probability that a randomly selected student scored more than 65 on the exam.

Use Online Normal calculator.

Mean = 63, SD =5,

Click above, enter 65.

Recalculate

P( X > 65 ) = 0.3446.

 

b) Find the probability that a score less than 85

Use Online Normal calculator. Mean = 63, SD =5,

Click below, enter 85.

Recalculate

P( X < 85 ) = 1

 

c) Find the 90^th percentile score.  ( top 10%)

Use Inverse Normal Calculator, mean = 63, SD = 5

Enter Area = 0.9, Click below

The cut-off X is at the below box.

 P(X < __69.4___) = 0.9. The 90th percentile is 69.4.

 

Ex2: Heights of men are normally distributed with mean of 68.6 in. and a standard deviation of 2.8 in.

Find the probability that a randomly selected man has a height greater than 72 in.

 Use Online Normal calculator.

Mean = 68.6, sd =2.8, Click above, enter 72.

Recalculate

P(X > 72) = 0.1123

 

Ex3. Given pulse rate of women is normally distributed with a mean of 74 bpm and a standard deviation of 12.5 bpm. Find the pulse rates of lowest 5% and highest 5% of women.

Total area = 5% + 5% =0.1

Find cutoff pulse rate for lowest 5% and highest 5%. Use Inverse Normal calculator.

Area = 0.10, Mean = 74, SD=12.5. Click Outside.

Recalculate. 

lowest 5% cutoff = 53.4 bpm highest 5%=94.6 bpm

Ex4. A circus farmer grows mandarin oranges finds that the diameters of mandarin oranges harvested on his farm follow a normal distribution with a mean diameter of 5.85 cm and standard deviation of 0.24cm.

a) Find the probability that a normally selected mandarin orange from his farm has a diameter larger than 6 cm.

Use Online Normal calculator.

Mean = 5.85, sd =0.24,

Click above, enter 6.

Recalculate

P( X > 6 ) = 0.266

b) Find the middle 20% diameter of mandarin oranges from his farm.

Use Inverse Normal Calculator

Area = 0.2, Mean = 5.85, sd=0.24

Click Between.

  P( _5.79____< X < __5.91____) = 0.2

Ex5. A TV has a life that is normally distributed with a mean of 6.5 years and a standard deviation of 2.3 years. If the company offers a warranty to replace any TV within 3 years. What percent of TV will need to be replaced?

To find percent, use Normal online calculator.

Mean = 6.5 , sd =2.3,

Click below, enter 3.

Recalculate

P (X < 3) = 0.064 = 6.4%