Ch 4.2 Application of Probability Distribution
- Page ID
- 15896
Ch 4.2 Application of Probability Distribution
Application of expected value.
The expected average gain or profit for a game or business in the long run.
X = Long term average net gain after a bet or Profit for a business, E(x) is expected gain for a game or a business after constructing a probability distribution.
Ex1. Suppose you play lottery where the chance of winning is 0.0001. You need to pay $3 to play. If you win, you will collect $10,000. What is the expected value of the game?
P(lose) = 1- P(win) = 1-0.0001 = 0.9999
Net win = 10,000 – 3 = 9997
Build a PD as below:
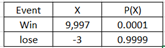
E(X) = \(\sum{xP(X)} = 9997(0.0001)+ (-3)(0.9999) = -2 \) (negative means loss)
In the long run, the expected loss per game is $2.
Ex1. Bet $5 on number 7 in roulette can be summarized below:
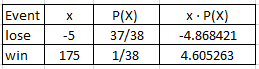
EV = E(X) = \(\sum{xP(X)} \) = -0.26 or 26 cents loss.
For every $5 bet, you can expect to lose an average of 26 cents.
Ex 3. The probability a 25- year- old male passes away within the year is .0.0005. He pays $275 for a one year $160000 life insurance policy. What is the expected value of the policy for the insurance company? Round your answer to the nearest cent.
From the insurance company’s point of view,
P(live) = 1 – P(die) = 1 – 0.0005 = 0.9995
If policy holder die, net loss = 275 - 160000 = -159725
Use the information to build the PD as follow
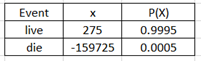
E(X) = 275(0.9995) + (-159725)(0.0005) = $195
In the long run, the company will gain $195 per policy.

