Ch 3.2 Independent and Mutually Exclusive Events
- Page ID
- 15892
Mutually exclusive events:
Two events are mutually exclusive (disjoint) if they will not occur at the same time. P(A and B) = 0
Ex1: Toss a 6-face die once, determine if the following are mutually exclusive:
a) Getting a “four” and “even”
No, four and even can occur at the same time, four and one are not mutually exclusive.
b) Getting a “four” and “five”
Yes, four and five cannot occur at the same time so four and five are mutually exclusive.
Ex2:
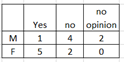
P(F and no opinion) = 0
F and no opinion are mutually exclusive so they cannot occur at the same time.
Independent Events:
Two events are independent when any of the following is true:
P(A and B) = P(A) ·P(B)
P(A) = P( A | B)
P(B) = P( B | A)
Ex1. Given a 2-way table below:
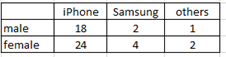
GT = 51
Is iPhone uses independent on gender?
Check if P(iPhone | female) = P( iPhone)
a) Find P(iPhone) = (18+24)/51 = 0.824
b) Find P(iPhone | female) = 24/30 = 0.8
P(iPhone) and P(iPhone Given female) are not exactly equal, so iPhone use is not independent of gender.
We can conclude that iPhone use is not independent on gender. Gender affect the choice of iPhone.
Ex2. Given a 2-way table below
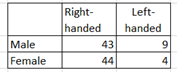 Grand total = 100
Grand total = 100
Is Right-handedness independent on gender?
Check if P(M and R) = P(M) · P (R )
P( M) = 52/100 = 0.52
P ( R ) = (43+44)/100 = 87/100 = 0.87
P(M and R) = 43/100 = 0.43
But P(M) · P( R) = 0.52 (0.87) = 0.45
So they are not exactly equal.
We can conclude they are not independent.
Note: we will visit this again in Ch 11 to take into consideration of sampling variation.
Note: mutually exclusive events are not necessarily independent events. They are two different concepts.

