Ch 3.1 Definitions and Terms
- Page ID
- 15891
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ch 3.1 and 3.2 Definitions and Terms:
Sample space (S): Total possible outcomes of a procedure. The outcomes are by chance and equally possible.
Event: outcome or result of a procedure. A, B, C ..
P(A) : probability of event A occurring.
Possible values for Probabilities
0 ≤ P(A) ≤ 1 (between 0 and 1, inclusive)
P(A) ≤ 0.05 , A is unlikely.
P(A) = 1, A is certain, P(A) = 0, A is impossible
P(A) = 0.5 : A has a 50-50 chance.
Three Approaches to find probability of an event A.
Approach 1: Theoretical probability
\( P(A)=\frac{\text{number of ways A occurs}}{\text{number of ways in sample space}} \)
All outcomes in the sample space are equally likely.
Example:
Ex1.: Select one card from a standard deck.
P(Heart) = 13/52 = ¼ = 0.25 = 25%
Ex 2: In a batch of 6500 light bulbs, 80 are defective.
Select one light bulb from the batch
P(defective) = 80/6500 = 0.0123
P(good) =(6500-80)/6500 = 0.988
Ex3: Find P(2 boys in three children family) ![]()
because sample space= {bbb, bbg, bgb, bgg, gbb, gbg, ggb, ggg}
P(2 boys) = 3/8
Approach 2: Relative frequency approximation
\( P(A)=\frac{\text{number of times A occurs}}{\text{number of times procedures were repeated}} \)
The probability is an estimate of chance.
Ex1: In year 2020, 86% of people use social media at least once per day. If one person is randomly selected, find the probability that the person uses social media at least once per day.
P( uses social media) = 0.86 (the relative frequency)
Ex2: A sample of 568 students shows 320 students are full-time student.
One student is selected from the whole population, find the probability of selecting a full time student.
a) P(full-time) = 320/568=0.563
Ex3: A batch of seed results in 78 white flowers and 65 pink flowers. Find probability of getting a white flower from planting the same type of seed.
P(white flower) = 78/(78+65) = 0.545
Ex4. Play Monty Hall game, what strategy gives a higher chance of winning?
http://www.shodor.org/interactivate/...mpleMontyHall/
Law of Large number: As the procedures are repeated more and more, the long term relative frequency approximation will get close to the theoretical probability.
Approach 3: Subjective approach
Use knowledge of the relevant circumstance to estimate the probability. May not be accurate.
Example: P(stuck in an elevator) = ??
This will probably be unlikely to occur, so Probability will likely be lower than 0.05.
Rounding and probability format:
Round to 3 significant digits unless fraction is a simple fraction of a/b where a, b are less than 10.
Use percentage only when communicating result to be the general public. Most software and professional journal use decimal notation.
Complement of Event A:
\( \bar{A} \) : Event A does not occur, complement of A.
\( P(\bar{A} ) = 1 - P(A) \)
Ex: There is 20% chance of rain today. What is the probability of not rain today?
P(not rain) = 1 – P(rain) = 1 – 0.2 = 0.8
“OR” of two simple events.
An outcome is in A or B if the outcome is in A or in B or both.
P(A or B) = Probability that A occurs, B occurs or both A and B occurs = \(\dfrac{\text{number of ways for A, B and both A and B}}{\text{ total number of ways}}\)
“AND” of two simple events.
An outcome is in A and B if the outcome is in both A and B.
P(A and B) = Probability that both A and B occurs at the same time = \(\dfrac{\text{number of ways for both A and B}}{\text{ total number of ways}}\)
Conditional probability
An event written as A given B is a conditional probability that A will occur given that B has already occurred.
P( A|B) = Probability that A occurs given that B has already occured = \(\dfrac{\text{number of ways for both A and B}}{\text{ total number of ways for B}}\)
P(A Given B) = P(A|B) = P( A and B)/ P(B)
Ex1. Toss a 6-face die once, find the probability that the outcome is
a) a “four”
b) a “four” or “five”
c) a “four” and “five”
d) a “four” given that the outcome is an “even” number.
e) a “prime number”
Answer: a) 1/6, b) 2/6, c) 0, d) 1/3, e) ½
Ex2. A marble jar has 5 red, 3 blue and 7 white marbles. If one marble is randomly selected, find
a) P(red)
b) P(not red)
c) P(red or blue)
d) P(red and blue)
e) P(red given blue)
Answer: a) 5/15 = 1/3 = 0.333 b) 10/15 = 0.667 c) 8/15 = 0.533 d) 0 e) 0
Ex3. One card is drawn from a standard deck, find the following probability:
a) P(black) = 26/52 = 0.5
b) P(black and A) = 2/52 = 0.0385
c) P( four) = 4/52 = 0.0769
d) P( black or A) = (26+2)/52 = 0.5385
e) P( king given black card) = 2/26 = 0.0769
f) P( A | diamond) = 1/13 = 0.0769
g) P( not face card) = 40/52 = 0.7692
Contingency table: (two-way table)
A table used to summarize two categorical variables of a set of data.
P( A) = \(\dfrac{\text{Total counts in row A or column A}}{\text{ Grand Total}}\)
P( A and B) = \(\dfrac{\text{sum of all counts in column A and row B}}{\text{ Grand Total}}\)
P(A or B) = \(\dfrac{\text{sum of all counts in colmnn A and row B}}{\text{ Grand Total}}\) (do not double count)
P(A given B) = \(\dfrac{\text{count that is intersection of A and B}}{\text{ Sum of counts of column B or row B}}\)
Ex1. Given the data, summarize into a contingency table
gra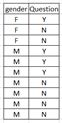
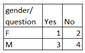 nd total = 10
nd total = 10
If one student is selected at random, use the contingency table to find the following probability
P(F) = (1+2)/10 = 0.3
P(No) = (2+4)/10 = 0.6
P(M and No) = 4/10 = 0.6
P(F and Y) = 1/10 =0.1
P(F or Y) = (1+2+3)/10 = 6/10 = 0.6
p(M or Y) = (3+4+1)/10 = 8/10 = 0.8
P(Yes GIVEN subject is male) = P(Y|M) = 3/7
Drug or clinical Diagnostic Test
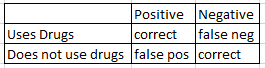
False positive: subject does not use drug but get a positive result.
False negative: subject uses drug but test does not detect it.
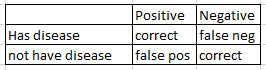
False positive: subject is not sick but get a positive result.
False negative: subject is sick but test does not detect it.
Ex1. Use the contingency table below, select one.
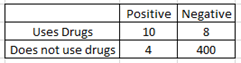
Find P(positive) = (10+4)/422 = 0.033
Find P(positive given that subject uses drugs)
= 10/(10+8) = 0.556
note: If the subject uses drug, there is a higher chance of getting positive result.

