Ch 4.2 Application of Probability Distribution

Last updated
Save as PDF

Page ID: 15896

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ch 4.2 Application of Probability Distribution

Application of expected value.

The expected average gain or profit for a game or business in the long run.

X = Long term average net gain after a bet or Profit for a business, E(x) is expected gain for a game or a business after constructing a probability distribution.

Ex1. Suppose you play lottery where the chance of winning is 0.0001. You need to pay $3 to play. If you win, you will collect $10,000. What is the expected value of the game?

P(lose) = 1- P(win) = 1-0.0001 = 0.9999

Net win = 10,000 – 3 = 9997

Build a PD as below:

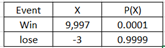
Probability distribution

E(X) = $\sum{xP(X)} = 9997(0.0001)+ (-3)(0.9999) = -2 $ (negative means loss)

In the long run, the expected loss per game is $2.

Ex1. Bet $5 on number 7 in roulette can be summarized below:

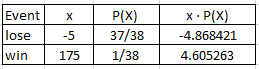
probability distribution

EV = E(X) = $\sum{xP(X)} $ = -0.26 or 26 cents loss.

For every $5 bet, you can expect to lose an average of 26 cents.

Ex 3. The probability a 25- year- old male passes away within the year is .0.0005. He pays $275 for a one year $160000 life insurance policy. What is the expected value of the policy for the insurance company? Round your answer to the nearest cent.

From the insurance company’s point of view,

P(live) = 1 – P(die) = 1 – 0.0005 = 0.9995

If policy holder die, net loss = 275 - 160000 = -159725

Use the information to build the PD as follow

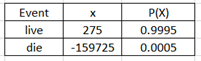
probability distribution

E(X) = 275(0.9995) + (-159725)(0.0005) = $195

In the long run, the company will gain $195 per policy.