9.5: A Population Proportion
- Page ID
- 27262
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)All hypotheses tests have the same basic steps:
- Determine the hypothesis: What are we trying to figure out? This is formally written as the null and alternative hypotheses.
- The alternative hypothesis, \(H_{a}\), never has a symbol that contains an equal sign.
- The alternative hypothesis, \(H_{a}\), tells you if the test is left, right, or two-tailed. It is the key to conducting the appropriate test.
- Calculate the evidence: This will be a test statistics and either a critical value or a p-value.
- In a hypothesis test problem, you may see words such as "the level of significance is 1%." The "1%" is the preconceived or preset \(\alpha\). The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data. If no level of significance is given, a common standard to use is \(\alpha = 0.05\).
- When you calculate the \(p\)-value and draw the picture, the \(p\)-value is the area in the left tail, the right tail, or split evenly between the two tails. For this reason, we call the hypothesis test left, right, or two tailed.
- Make a decision: The options will be Reject the Null Hypothesis or Do not Reject the Null Hypothesis.
- Never, ever, Accept the Null Hypothesis.
- Thinking about the meaning of the \(p\)-value: A data analyst (and anyone else) should have more confidence that he made the correct decision to reject the null hypothesis with a smaller \(p\)-value (for example, 0.001 as opposed to 0.04) even if using the 0.05 level for alpha. Similarly, for a large p-value such as 0.4, as opposed to a \(p\)-value of 0.056 (\(\alpha = 0.05\) is less than either number), a data analyst should have more confidence that she made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.
- Determine the conclusion: What does the decision mean in terms of the problem given?
Proportions
Proportions are part of a whole. Just like with confidence intervals, we can make inferences using hypothesis tests involving proportions.
Full Hypothesis Test Examples
Joon believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50%. Joon samples 100 first-time brides and 53 reply that they are younger than their grooms. For the hypothesis test, she uses a 1% level of significance.
\(P\)-value Solution
Determine the hypothesis:
A 1% level of significance means that \(\alpha = 0.01\). This is a test of a single population proportion.
\(H_{0}: p = 0.50\)
\(H_{a}: p \neq 0.50\) (claim)
The words, "is the same or different from" indicates a two-tailed test, giving a \(\neq\) in the alternative hypothesis.
Calculate the evidence:
The problem contains no mention of a mean. The information is given in terms of percentages. Use the formulas for \(\hat{p}\), the estimated proportion.
Calculate the test statistic using the formula for a \(z\) proportion test.
\[z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\nonumber\]
\(p=0.50\) comes from \(H_{0}\). \(\hat{p}=\frac{53}{100}=0.53\) comes from the sample, and \(n=100\).
\[z=\frac{0.53-0.50}{\sqrt{\frac{0.50(1-0.50)}{100}}}=\frac{0.03}{\sqrt{\frac{0.50(0.50)}{100}}}=\frac{0.03}{\sqrt{\frac{0.25}{100}}}=\frac{0.03}{\sqrt{0.0025}}=\frac{0.03}{0.05}=0.6\nonumber\]
Now calculate the \(p\)-value based on the test statistic found.
This is a two-tailed test, using the \(z\) distribution, so use the Excel formula \(=2*(1-\text{NORM.S.DIST}(z,\text{true}))\).
In this problem we found \(z\), which is the test statistic, to be \(z=0.6\).
Use the Excel formula \(=2*(1-\text{NORM.S.DIST}(0.6,\text{true}))=0.5485\).
Interpretation of the \(p\)-value: If the null hypothesis is true, there is 0.5485 probability (54.85%) that the sample (estimated) proportion \(\hat{p}\) is 0.53 or more OR 0.47 or less (see the graph in Figure).
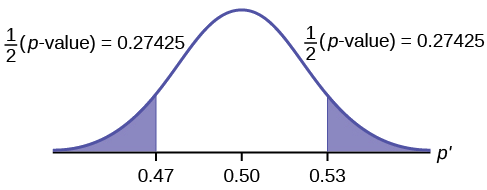
Make a decision:
\(\alpha\) is the minimum area that could be considered to make our result significant.
Compare \(\alpha\) and the \(p-\text{value}\)
- If \(p\)-value is less than the \(\alpha\) then we will Reject \(H_{0}\).
- If \(\alpha\) is less than the \(p\)-value then we will Fail to Reject \(H_{0}\).
Compare \(\alpha = 0.01\) and \(p\text{-value} = 0.5485\).
Since \(p\)-value \(>\alpha\), do not reject \(H_{0}\)
This means you do not reject \(p = 0.50\).
Conclusion:
At a 1% level of significance, the sample data do not show sufficient evidence that 50% of first time brides in the US are younger than their grooms.
Critical Value Solution
Determine the hypothesis (Same as the \(P\)-value solution):
A 1% level of significance means that \(\alpha = 0.01\). This is a test of a single population proportion.
\(H_{0}: p = 0.50\)
\(H_{a}: p \neq 0.50\) (claim)
The words, "is the same or different from" indicates a two-tailed test, giving a \(\neq\) in the alternative hypothesis.
Calculate the evidence:
The problem contains no mention of a mean. The information is given in terms of percentages. Use the formulas for \(\hat{p}\), the estimated proportion.
Calculate the critical value. Since this is a two-tailed test, using the \(z\) distribution, so use the Excel formula \(=\text{NORM.S.INV}(1-\alpha/2)\).
In this problem, \(\alpha=0.01\).
Use the Excel formula, \(=\text{NORM.S.INV}(1-0.01/2)=2.5758.\)
This is a two-tailed test, so there will be two critical values, \(-2.5758\) and \(2.5758\).
Now, calculate the test statistic using the formula for a \(z\) proportion test.
\[z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\nonumber\]
\(p=0.50\) comes from \(H_{0}\). \(\hat{p}=\frac{53}{100}=0.53\) comes from the sample, and \(n=100\).
\[z=\frac{0.53-0.50}{\sqrt{\frac{0.50(1-0.50)}{100}}}=\frac{0.03}{\sqrt{\frac{0.50(0.50)}{100}}}=\frac{0.03}{\sqrt{\frac{0.25}{100}}}=\frac{0.03}{\sqrt{0.0025}}=\frac{0.03}{0.05}=0.6\nonumber\]
Make a decision:
Graph the critical value and the test statistic along the number line of the Standard Normal Distribution graph.
Since this is two-tailed, everything less than the negative critical value, \(\text{CV}=-2.5758\), and everything greater than the positive critical value, \(\text{CV}=2.5758\) will be the rejection region.
Since the test statistic, \(z=0.6\) is not less than the negative critical value, \(\text{CV}=-2.5758\), or greater than the positive critical value, \(\text{CV}=2.5758\), the decision will be to Fail to Reject the Null Hypothesis.
Conclusion (Same as the \(P\)-value solution):
At a 1% level of significance, the sample data do not show sufficient evidence that 50% of first time brides in the US are younger than their grooms.
The Type I and Type II errors:
The Type I error is to conclude that the proportion of first-time brides who are younger than their grooms is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true).
The Type II error is there is not enough evidence to conclude that the proportion of first time brides who are younger than their grooms differs from 50% when, in fact, the proportion does differ from 50%. (Do not reject the null hypothesis when the null hypothesis is false.)
A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance and the \(p\)-value method.
Answer
Determine the hypothesis:
A 1% level of significance means that \(\alpha = 0.01\). This is a test of a single population proportion.
\(H_{0}: p = 0.85\)
\(H_{a}: p \neq 0.85\) (claim)
The words, "is the same or different from" indicates a two-tailed test, giving a \(\neq\) in the alternative hypothesis.
Calculate the evidence:
The problem contains no mention of a mean. The information is given in terms of percentages. Use the formulas for \(\hat{p}\), the estimated proportion.
Calculate the test statistic using the formula for a \(z\) proportion test.
\[z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\nonumber\]
\(p=0.85\) comes from \(H_{0}\). \(\hat{p}=\frac{39}{50}=0.78\) comes from the sample, and \(n=50\).
\[z=\frac{0.78-0.85}{\sqrt{\frac{0.85(1-0.85)}{50}}}=\frac{-0.07}{\sqrt{\frac{0.85(0.15)}{50}}}=\frac{-0.07}{\sqrt{\frac{0.1275}{50}}}=\frac{-0.07}{\sqrt{0.00255}}=\frac{-0.07}{0.0505}=-1.386\nonumber\]
Now calculate the \(p\)-value based on the test statistic found.
This is a two-tailed test, using the \(z\) distribution, so use the Excel formula \(=2*(1-\text{NORM.S.DIST}(z,\text{true}))\).
In this problem we found \(z\), which is the test statistic, to be \(z=-1.386\). Always use the positive of the test statistic in the two-tailed Excel formula.
Use the Excel formula \(=2*(1-\text{NORM.S.DIST}(1.386,\text{true}))=0.1657\).
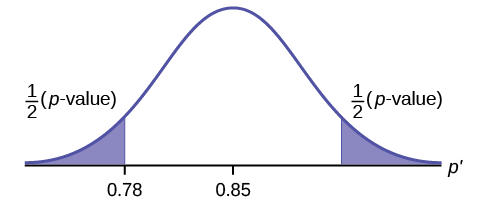
Make a decision:
\(\alpha\) is the minimum area that could be considered to make our result significant.
Compare \(\alpha\) and the \(p-\text{value}\)
- If \(p\)-value is less than the \(\alpha\) then we will Reject \(H_{0}\).
- If \(\alpha\) is less than the \(p\)-value then we will Fail to Reject \(H_{0}\).
Compare \(\alpha = 0.01\) and \(p\text{-value} = 0.1657\).
Since \(p\)-value \(>\alpha\), do not reject \(H_{0}\)
This means you do not reject \(p = 0.85\).
Conclusion:
At a 1% level of significance, the sample data do not show there is sufficient evidence to suggest that the proportion of students that want to go to the zoo is not 85%.
Suppose a consumer group suspects that the proportion of households that have three cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a critical value hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three cell phones.
Answer
Determine the hypothesis:
Since the level of significance is not given in the problem, we should assume that \(\alpha = 0.05\). This is a test of a single population proportion.
\(H_{0}: p = 0.30\)
\(H_{a}: p \neq 0.30\) (claim)
The \(\neq\) in the alternative hypothesis tells us this is a two-tailed test.
Calculate the evidence:
The problem contains no mention of a mean. The information is given in terms of percentages. Use the formulas for \(\hat{p}\), the estimated proportion.
Calculate the critical value. Since this is a two-tailed test, using the \(z\) distribution, so use the Excel formula \(=\text{NORM.S.INV}(1-\alpha/2)\).
In this problem, \(\alpha=0.05\).
Use the Excel formula, \(=\text{NORM.S.INV}(1-0.05/2)=1.9600.\)
This is a two-tailed test, so there will be two critical values, \(-1.96\) and \(1.96\).
Now, calculate the test statistic using the formula for a \(z\) proportion test.
\[z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\nonumber\]
\(p=0.30\) comes from \(H_{0}\). \(\hat{p}=\frac{43}{150}=0.2867\) comes from the sample, and \(n=150\).
\[z=\frac{0.2867-0.30}{\sqrt{\frac{0.30(1-0.30)}{150}}}=\frac{-0.0133}{\sqrt{\frac{0.30(0.70)}{150}}}=\frac{-0.0133}{\sqrt{\frac{0.21}{150}}}=\frac{-0.0133}{\sqrt{0.0014}}=\frac{-0.0133}{0.0374}=-0.3555\nonumber\]
Make a decision:
Graph the critical value and the test statistic along the number line of the Standard Normal Distribution graph.
Since this is two-tailed, everything less than the negative critical value, \(\text{CV}=-1.96\), and everything greater than the positive critical value, \(\text{CV}=1.96\) will be the rejection region.
Since the test statistic, \(z=-0.3555\) is not less than the negative critical value, \(\text{CV}=-2.5758\), or greater than the positive critical value, \(\text{CV}=2.5758\), the decision will be to Fail to Reject the Null Hypothesis.
Conclusion:
At a 5% level of significance, the sample data do not show sufficient evidence to conclude that the proportion of households who own 3 cell phones is not 30%.
Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 10% level of significance. State the null and alternative hypothesis, find the p-value, state your conclusion, and identify the Type I and Type II errors.
Answer
Determine the hypothesis:
A 10% level of significance means that \(\alpha = 0.10\). This is a test of a single population proportion.
\(H_{0}: p \geq 0.92\)
\(H_{a}: p < 0.92\) (claim)
The \(<\) in the alternative hypothesis indicates this is a left-tail test.
Calculate the evidence:
The problem contains no mention of a mean. The information is given in terms of percentages. Use the formulas for \(\hat{p}\), the estimated proportion.
Calculate the critical value. Since this is a left-tailed test, using the \(z\) distribution, so use the Excel formula \(=\text{NORM.S.INV}(\alpha)\).
In this problem, \(\alpha=0.10\).
Use the Excel formula, \(=\text{NORM.S.INV}(0.10)=-1.28155.\)
Now, calculate the test statistic using the formula for a \(z\) proportion test.
\[z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\nonumber\]
\(p=0.92\) comes from \(H_{0}\). \(\hat{p}=\frac{174}{200}=0.87\) comes from the sample, and \(n=200\).
\[z=\frac{0.87-0.92}{\sqrt{\frac{0.92(1-0.92)}{200}}}=\frac{-0.05}{\sqrt{\frac{0.92(0.08)}{200}}}=\frac{-0.05}{\sqrt{\frac{0.0736}{200}}}=\frac{-0.05}{\sqrt{0.000368}}=\frac{-0.05}{0.01918}=-2.6064\nonumber\]
Make a decision:
Graph the critical value and the test statistic along the number line of the Standard Normal Distribution graph.
Since this is left-tailed, everything to the left of, that is less than the critical value, \(\text{CV}=-1.28155\) will be the rejection region.
Since the test statistic, \(z=-2.6064\) is less than the critical value, \(\text{CV}=-1.28155\) the decision will be to Reject the Null Hypothesis.
Conclusion:
At a 10% level of significance, there is sufficient sample evidence to conclude that fewer than 92% of American adults own cell phones.
Type I and Type II Errors:
Type I Error: To conclude that fewer than 92% of American adults own cell phones when, in fact, 92% of American adults do own cell phones (reject the null hypothesis when the null hypothesis is true).
Type II Error: To conclude that 92% of American adults own cell phones when, in fact, fewer than 92% of American adults own cell phones (do not reject the null hypothesis when the null hypothesis is false).
The next example is a poem written by a statistics student named Nicole Hart. The solution to the problem follows the poem. Notice that the hypothesis test is for a single population proportion. This means that the null and alternate hypotheses use the parameter \(p\). The distribution for the test is normal. The estimated proportion \(\hat{p}\) is the proportion of fleas killed to the total fleas found on Fido. This is sample information. The problem gives a preconceived \(\alpha = 0.01\), for comparison. The poem is clever and humorous, so please enjoy it!
My dog has so many fleas,
They do not come off with ease.
As for shampoo, I have tried many types
Even one called Bubble Hype,
Which only killed 25% of the fleas,
Unfortunately I was not pleased.
I've used all kinds of soap,
Until I had given up hope
Until one day I saw
An ad that put me in awe.
A shampoo used for dogs
Called GOOD ENOUGH to Clean a Hog
Guaranteed to kill more fleas.
I gave Fido a bath
And after doing the math
His number of fleas
Started dropping by 3's!
Before his shampoo
I counted 42.
At the end of his bath,
I redid the math
And the new shampoo had killed 17 fleas.
So now I was pleased.
Now it is time for you to have some fun
With the level of significance being .01,
You must help me figure out
Use the new shampoo or go without?
Answer
Determine the hypothesis:
A 1% level of significance means that \(\alpha = 0.01\). This is a test of a single population proportion.
\(H_{0}: p \leq 0.25\)
\(H_{a}: p > 0.25\) (claim)
The \(>\) in the alternative hypothesis indicates a right-tailed test.
Calculate the evidence:
The problem contains no mention of a mean. The information is given in terms of percentages. Use the formulas for \(\hat{p}\), the estimated proportion.
Calculate the test statistic using the formula for a \(z\) proportion test.
\[z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\nonumber\]
\(p=0.25\) comes from \(H_{0}\). \(\hat{p}=\frac{17}{42}=0.4047\) comes from the sample, and \(n=42\).
\[z=\frac{0.4047-0.25}{\sqrt{\frac{0.25(1-0.25)}{42}}}=\frac{0.1548}{\sqrt{\frac{0.25(0.75)}{42}}}=\frac{0.1548}{\sqrt{\frac{0.1875}{42}}}=\frac{0.1548}{\sqrt{0.004464}}=\frac{0.1548}{0.0668}=2.3163\nonumber\]
Now calculate the \(p\)-value based on the test statistic found.
This is a right-tailed test, using the \(z\) distribution, so use the Excel formula \(=1-\text{NORM.S.DIST}(z,\text{true})\).
In this problem we found \(z\), which is the test statistic, to be \(z=2.3163\).
Use the Excel formula \(=1-\text{NORM.S.DIST}(0.6,\text{true})=0.0103\).
Interpretation of the \(p\)-value: If the null hypothesis is true, there is 0.5485 probability (54.85%) that the sample (estimated) proportion \(\hat{p}\) is 0.53 or more OR 0.47 or less (see the graph in Figure).
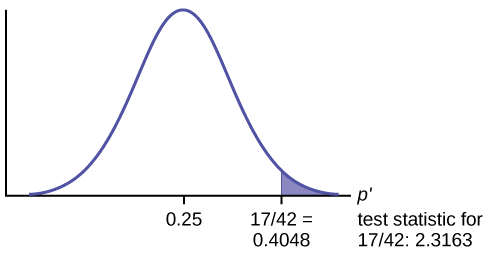
Make a decision:
\(\alpha\) is the minimum area that could be considered to make our result significant.
Compare \(\alpha\) and the \(p-\text{value}\)
- If \(p\)-value is less than the \(\alpha\) then we will Reject \(H_{0}\).
- If \(\alpha\) is less than the \(p\)-value then we will Fail to Reject \(H_{0}\).
Compare \(\alpha = 0.01\) and \(p\text{-value} = 0.0103\).
Since \(p\)-value \(>\alpha\), do not reject \(H_{0}\)
This means you do not reject \(p = 0.25\).
Conclusion:
At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of fleas that are killed by the new shampoo is more than 25%.
This test result is not very definitive since the \(p\text{-value}\) is very close to alpha. In reality, one would probably do more tests by giving the dog another bath after the fleas have had a chance to return.
In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim, using the critical value method, that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.
Answer
Determine the hypothesis:
A 0.005 level of significance means that \(\alpha = 0.005\). This is a test of a single population proportion.
\(H_{0}: p \leq 0.00034\)
\(H_{a}: p > 0.00034\) (claim)
Since the alternative hypothesis has a \(>\), this will be a right-tailed test.
Calculate the evidence:
The problem contains no mention of a mean. The information is given in terms of percentages. Use the formulas for \(\hat{p}\), the estimated proportion.
Calculate the critical value. Since this is a right-tailed test, using the \(z\) distribution, so use the Excel formula \(=\text{NORM.S.INV}(1-\alpha)\).
In this problem, \(\alpha=0.005\).
Use the Excel formula, \(=\text{NORM.S.INV}(1-0.005)=2.5758.\)
Now, calculate the test statistic using the formula for a \(z\) proportion test.
\[z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\nonumber\]
\(p=0.00034\) comes from \(H_{0}\). \(\hat{p}=\frac{172}{420,019}=0.0004095\) comes from the sample, and \(n=420,019\).
\[z=\frac{0.0004095-0.00034}{\sqrt{\frac{0.00034(1-0.00034)}{420,019}}}=\frac{0.0000695}{\sqrt{\frac{0.00034(0.99966)}{420,019}}}=\frac{0.0000695}{\sqrt{\frac{0.0003399}{420,019}}}=\frac{0.0000695}{\sqrt{0.00000000081}}=\frac{0.0003399}{0.0.000028}=2.4433\nonumber\]
Make a decision:
Graph the critical value and the test statistic along the number line of the Standard Normal Distribution graph.
Since this is right-tailed, everything greater than the critical value, \(\text{CV}=2.5758\) will be the rejection region.
Since the test statistic, \(z=2.4433\) is not greater than the critical value, \(\text{CV}=2.5758\) the decision will be to Fail to Reject the Null Hypothesis.
Conclusion:
We conclude that there is not enough evidence to support the claim of higher brain cancer rates for the cell phone users.
Type 1 error:
If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.
According to the US Census there are approximately 268,608,618 residents aged 12 and older. Statistics from the Rape, Abuse, and Incest National Network indicate that, on average, 207,754 rapes occur each year (male and female) for persons aged 12 and older. This translates into a percentage of sexual assaults of 0.078%. In Daviess County, KY, there were reported 11 rapes for a population of 37,937. Conduct a \(p\)-value hypothesis test to determine if there is a statistically significant difference between the local sexual assault percentage and the national sexual assault percentage. Use a significance level of 0.01.
Answer
Determine the hypothesis:
A 0.01 level of significance means that \(\alpha = 0.01\). This is a test of a single population proportion.
\(H_{0}: p = 0.00078\)
\(H_{a}: p \neq 0.00078\) (claim)
Since the alternative hypothesis says \(\neq\) this will be a two-tailed test.
Calculate the evidence:
The problem contains no mention of a mean. The information is given in terms of percentages. Use the formulas for \(\hat{p}\), the estimated proportion.
Calculate the test statistic using the formula for a \(z\) proportion test.
\[z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\nonumber\]
\(p=0.00078\) comes from \(H_{0}\). \(\hat{p}=\frac{11}{37,937}=0.00029\) comes from the sample, and \(n=37,937\).
\[z=\frac{0.00029-0.00078}{\sqrt{\frac{0.00078(1-0.00078)}{37,937}}}=\frac{-0.00049}{\sqrt{\frac{0.00078(0.99922)}{37,937}}}=\frac{-0.00049}{\sqrt{\frac{0.000779}{37,937}}}=\frac{-0.00049}{\sqrt{0.000000021}}=\frac{-0.00049}{0.0001433}=-3.4186\nonumber\]
Now calculate the \(p\)-value based on the test statistic found.
This is a two-tailed test, using the \(z\) distribution, so use the Excel formula \(=2*(1-\text{NORM.S.DIST}(z,\text{true}))\).
In this problem we found \(z\), which is the test statistic, to be \(z=-3.4186\).
Always use the positive number in the two-tailed formula, \(3.4186\)
Use the Excel formula \(=2*(1-\text{NORM.S.DIST}(3.4186,\text{true}))=0.00063\).
Make a decision:
\(\alpha\) is the minimum area that could be considered to make our result significant.
Compare \(\alpha\) and the \(p-\text{value}\)
- If \(p\)-value is less than the \(\alpha\) then we will Reject \(H_{0}\).
- If \(\alpha\) is less than the \(p\)-value then we will Fail to Reject \(H_{0}\).
Compare \(\alpha = 0.01\) and \(p\text{-value} = 0.00063\).
Since \(p\)-value \(<\alpha\), reject \(H_{0}\)
This means you reject \(p = 0.00078\).
Conclusion:
At a 1% level of significance, the sample data support the claim that the proportion of sexual assaults in Daviess County, Kentucky is different from the national average proportion.
Review
The hypothesis test itself has an established process. This can be summarized as follows:
- Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
- Determine the random variable.
- Determine the distribution for the test.
- Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A z-score and a t-score are examples of test statistics.)
- Compare the preconceived α with the p-value, make a decision (reject or do not reject H0), and write a clear conclusion using English sentences.
Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test. A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.
References
- Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
- Data from Bloomberg Businessweek. Available online at www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
- Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
- Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
- Data from Growing by Degrees by Allen and Seaman.
- Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
- Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
- Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
- Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm.
- Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
- Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
- Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
- Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1.
- Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
- Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
- “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
- Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
- Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).
Glossary
- Central Limit Theorem
- Given a random variable (RV) with known mean \(\mu\) and known standard deviation \(\sigma\). We are sampling with size \(n\) and we are interested in two new RVs - the sample mean, \(\bar{X}\), and the sample sum, \(\sum X\). If the size \(n\) of the sample is sufficiently large, then \(\bar{X} - N\left(\mu, \frac{\sigma}{\sqrt{n}}\right)\) and \(\sum X - N \left(n\mu, \sqrt{n}\sigma\right)\). If the size n of the sample is sufficiently large, then the distribution of the sample means and the distribution of the sample sums will approximate a normal distribution regardless of the shape of the population. The mean of the sample means will equal the population mean and the mean of the sample sums will equal \(n\) times the population mean. The standard deviation of the distribution of the sample means, \(\frac{\sigma}{\sqrt{n}}\), is called the standard error of the mean.
Contributors and Attributions
Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/30189442-699...b91b9de@18.114.


