Probability and Independence
- Page ID
- 217
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)For an experiment we define an event to be any collection of possible outcomes. A simple event is an event that consists of exactly one outcome.
- "or" means the union (i.e. either can occur)
- "and" means intersection (i.e. both must occur)
Two events are mutually exclusive if they cannot occur simultaneously. For a Venn diagram, we can tell that two events are mutually exclusive if their regions do not intersect
We define probability of an event \(E\) to be to be
\[P(E) = \dfrac{\text{number of simple events within E}}{\text{ total number of possible outcomes}} \nonumber \]
We have the following:
- \(P(E)\) is always between 0 and 1.
- The sum of the probabilities of all simple events must be 1.
- \(P(E) + P(\text{not } E) = 1\)
- If \(E\) and \(F\) are mutually exclusive then
\[ P(E \text{ or } F) = P(E) + P(F) \nonumber \]
The Difference Between "and" and "or"
If \(E\) and \(F\) are events then we use the terminology
\[ E \text{ and } F \nonumber \]
to mean all outcomes that belong to both \(E\) and \(F\).
We use the terminology
\[E \text{ or } F \nonumber \]
to mean all outcomes that belong to either \(E\) or \(F\).
Below is an example of two sets, \(A\) and \(B\), graphed in a Venn diagram.
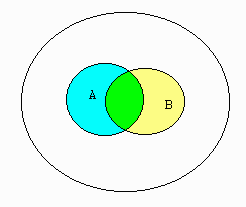
The green area represents \(A\) and \(B\) while all areas with color represent \(A\) or \(B\)
Our Women's Volleyball team is recruiting for new members. Suppose that a person inquires about the team.
- Let \(E\) be the event that the person is female
- Let \(F\) be the event that the person is a student
then \(E\) and \(F\) represents the qualifications for being a member of the team. Note that \(E\) or \(F\) is not enough.
We define
\[ P(E|F) = \dfrac{P(E \text{ and } F}{P(F)} \nonumber \]
We read the left hand side as "The probability of event \(E\) given event \(F\) occurred."
We call two events independent if the following definitions hold.
For independent Events
\[P(E|F) = P(E) \label{1a} \]
Equivalently, we can say that \(E\) and \(F\) are independent if
For Independent Events
\[P(E \text{ and } F) = P(E)P(F) \label{1b} \]
Consider rolling two dice. Let
- \(E\) be the event that the first die is a 3.
- \(F\) be the event that the sum of the dice is an 8.
Then \(E\) and \(F\) means that we rolled a three and then we rolled a 5
This probability is 1/36 since there are 36 possible pairs and only one of them is (3,5)
We have
\[ P(E) = 1/6 \nonumber \]
And note that (2,6),(3,5),(4,4),(5,3), and (6,2) give \(F\)
Hence
\[ P(F) = 5/36 \nonumber \]
We have
\[ P(E) P(F) = (1/6) (5/36) \nonumber \]
which is not 1/36 and we can conclude that \(E\) and \(F\) are not independent.
Test the following two events for independence:
- \(E\) the event that the first die is a 1.
- \(F\) the event that the sum is a 7.
A Counting Rule
For two events, \(E\) and \(F\), we always have
\[ P(E \text{ or } F) = P(E) + P(F) - P(E \text{ and } F) \label{2} \]
Find the probability of selecting either a heart or a face card from a 52 card deck.
Solution
We let
- \(E\) = the event that a heart is selected
- \(F\) = the event that a face card is selected
then
\[ P(E) = \dfrac{1}{4} \nonumber \]
and
\[ P(F) = \dfrac{3}{13} \nonumber \]
that is, Jack, Queen, or King out of 13 different cards of one kind.
\[ P(E \text{ and } F) = \dfrac{3}{52} \nonumber \]
The counting rule formula (eq. 2) gives
\[ P(E \text{ or } F) = \dfrac{1}{4} + \dfrac{3}{13} - \dfrac{3}{52} = \dfrac{22}{52} = 42\text{%} \nonumber \]
Contributors
- Larry Green (Lake Tahoe Community College)