10.4: Problems on Functions of Random Variables

Last updated
Save as PDF

Page ID: 10879

Paul Pfeiffer
Rice University

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Exercise $\PageIndex{1}$

Suppose $X$ is a nonnegative, absolutely continuous random variable. Let $Z = g(X) = Ce^{-aX}$, where $a > 0$, $C > 0$. Then $0 < Z \le C$. Use properties of the exponential and natural log function to show that

$F_Z (v) = 1 - F_X (- \dfrac{\text{In } (v/C)}{a})$ for $0 < v \le C$

Answer

$Z = Ce^{-aX} \le v$ iff $e^{-aX} \le v/C$ iff $-aX \le \text{In } (v/C)$ iff $X \ge - \text{In } (v/C)/a$, so that

$F_Z(v) = P(Z \le v) = P(X \ge -\text{In } (v/C)/a) = 1 - F_X (-\dfrac{\text{In } (v/C)}{a})$

Exercise $\PageIndex{2}$

Use the result of Exercise 10.4.1 to show that if $X$ ~ exponential $(\lambda)$, then

$F_Z (v) = (\dfrac{v}{C})^{\lambda/a}$ $0 < v \le C$

Answer: $F_Z (v) = 1 - [1- exp (-\dfrac{\lambda}{a} \cdot \text{In } (v/C))] = (\dfrac{v}{C})^{\lambda/a}$

Exercise $\PageIndex{3}$

Present value of future costs. Suppose money may be invested at an annual rate a, compounded continually. Then one dollar in hand now, has a value $e^{ax}$ at the end of $x$ years. Hence, one dollar spent $x$ years in the future has a present valuee$^{-ax}$. Suppose a device put into operation has time to failure (in years) $X$ ~ exponential ($\lambda$). If the cost of replacement at failure is $C$ dollars, then the present value of the replacement is $Z = Ce^{-aX}$. Suppose $\lambda = 1/10$, $a = 0.07$, and $C =$ $1000.

Use the result of Exercise 10.4.2. to determine the probability $Z \le 700, 500, 200$.
Use a discrete approximation for the exponential density to approximate the probabilities in part (a). Truncate $X$ at 1000 and use 10,000 approximation points.

Answer

$P(Z \le v) = (\dfrac{v}{1000})^{10/7}$

v = [700 500 200];
P = (v/1000).^(10/7)
P =  0.6008    0.3715    0.1003
tappr
Enter matrix [a b] of x-range endpoints  [0 1000]
Enter number of x approximation points  10000
Enter density as a function of t  0.1*exp(-t/10)
Use row matrices X and PX as in the simple case
G = 1000*exp(-0.07*t);
PM1 = (G<=700)*PX'
PM1 =  0.6005
PM2 = (G<=500)*PX'
PM2 =  0.3716
PM3 = (G<=200)*PX'
PM3 =  0.1003

Exercise $\PageIndex{4}$

Optimal stocking of merchandise. A merchant is planning for the Christmas season. He intends to stock m units of a certain item at a cost of c per unit. Experience indicates demand can be represented by a random variable $D$ ~ Poisson ($\mu$). If units remain in stock at the end of the season, they may be returned with recovery of $r$ per unit. If demand exceeds the number originally ordered, extra units may be ordered at a cost of s each. Units are sold at a price $p$ per unit. If $Z = g(D)$ is the gain from the sales, then

For $t \le m$, $g(t) = (p - c) t- (c - r)(m - t) = (p - r)t + (r - c) m$
For $t > m$, $g(t) = (p - c)m + (t - m) (p - s) = (p - s) t + (s - c)m$

Let $M = (-\infty, m]$. Then

$g(t) = I_M(t) [(p - r) t + (r - c)m] + I_M(t) [(p - s) t + (s - c) m]$

Suppose $\mu = 50$ $m = 50$ $c = 30$ $p = 50$ $r = 20$ $s = 40$.

Approximate the Poisson random variable $D$ by truncating at 100. Determine $P(500 \le Z \le 1100)$.

Answer

mu = 50;
D = 0:100;
c = 30;
p = 50;
r = 20;
s = 40;
m = 50;
PD = ipoisson(mu,D);
G = (p - s)*D + (s - c)*m +(s - r)*(D - m).*(D <= m);
M = (500<=G)&(G<=1100);
PM = M*PD'
PM =  0.9209
 
[Z,PZ] = csort(G,PD);         % Alternate: use dbn for Z
m = (500<=Z)&(Z<=1100);
pm = m*PZ'
pm =  0.9209

Exercise $\PageIndex{5}$

(See Example 2 from "Functions of a Random Variable") The cultural committee of a student organization has arranged a special deal for tickets to a concert. The agreement is that the organization will purchase ten tickets at $20 each (regardless of the number of individual buyers). Additional tickets are available according to the following schedule:

11-20, $18 each
21-30, $16 each
31-50, $15 each
51-100, $13 each

If the number of purchasers is a random variable $X$, the total cost (in dollars) is a random quantity $Z = g(X)$ described by

$g(X) = 200 + 18 I_{M1} (X) (X - 10) + (16 - 18) I_{M2} (X) (X - 20) +$

$(15 - 16) I_{M_3} (X) (X - 30) + (13 - 15) I_{M4} (X) (X - 50)$

where $M1 = [10, \infty)$, $M2 = [20, \infty)$, $M3 = [30, \infty)$, $M4 = [50, \infty)$

Suppose $X$~ Poisson (75). Approximate the Poisson distribution by truncating at 150. Determine $P(Z \ge 1000)$, $P(Z \ge 1300)$ and $P(900 \le Z \le 1400)$.

Answer

X = 0:150;
PX = ipoisson(75,X);
G = 200 + 18*(X - 10).*(X>=10) + (16 - 18)*(X - 20).*(X>=20) + ...
     (15 - 16)*(X- 30).*(X>=30) + (13 - 15)*(X - 50).*(X>=50);
P1 = (G>=1000)*PX'
P1 =  0.9288
P2 = (G>=1300)*PX'
P2 =  0.1142
P3 = ((900<=G)&(G<=1400))*PX'
P3 =  0.9742
[Z,PZ] = csort(G,PX);         % Alternate: use dbn for Z
p1 = (Z>=1000)*PZ'
p1 =  0.9288

Exercise $\PageIndex{6}$

(See Exercise 6 from "Problems on Random Vectors and Joint Distributions", and Exercise 1 from "Problems on Independent Classes of Random Variables")) The pair $\{X, Y\}$ has the joint distribution

(in m-file npr08_06.m):

$X = $ [-2.3 -0.7 1.1 3.9 5.1] $Y = $ [1.3 2.5 4.1 5.3]

$P = \begin{bmatrix} 0.0483 & 0.0357 & 0.0420 & 0.0399 & 0.0441 \\ 0.0437 & 0.0323 & 0.0380 & 0.0361 & 0.0399 \\ 0.0713 & 0.0527 & 0.0620 & 0.0609 & 0.0551 \\ 0.0667 & 0.0493 & 0.0580 & 0.0651 & 0.0589 \end{bmatrix}$

Determine $P(\text{max }\{X, Y\} \le 4)$. Let $Z = 3X^3 + 3X^2 Y - Y^3$.

Determine $P(Z< 0)$ and $P(-5 < Z \le 300)$.

Answer

npr08_06
Data are in X, Y, P
jcalc
Enter JOINT PROBABILITIES (as on the plane)  P
Enter row matrix of VALUES of X  X
Enter row matrix of VALUES of Y  Y
 Use array operations on matrices X, Y, PX, PY, t, u, and P
P1 = total((max(t,u)<=4).*P)
P1 =  0.4860
P2 = total((abs(t-u)>3).*P)
P2 =  0.4516
G = 3*t.^3 + 3*t.^2.*u - u.^3;
P3 = total((G<0).*P)
P3 =  0.5420
P4 = total(((-5<G)&(G<=300)).*P)
P4 =  0.3713
[Z,PZ] = csort(G,P);          % Alternate: use dbn for Z
p4 = ((-5<Z)&(Z<=300))*PZ'
p4 =  0.3713

Exercise $\PageIndex{7}$

(See Exercise 2 from "Problems on Independent Classes of Random Variables") The pair $\{X, Y\}$ has the joint distribution (in m-file npr09_02.m):

$X = $ [-3.9 -1.7 1.5 2 8 4.1] $Y = $ [-2 1 2.6 5.1]

$P = \begin{bmatrix} 0.0589 & 0.0342 & 0.0304 & 0.0456 & 0.0209 \\ 0.0962 & 0.056 & 0.0498 & 0.0744 & 0.0341 \\ 0.0682 & 0.0398 & 0.0350 & 0.0528 & 0.0242 \\ 0.0868 & 0.0504 & 0.0448 & 0.0672 & 0.0308 \end{bmatrix}$

Determine $P(\{X + Y \ge 5\} \cup \{Y \le 2\})$, $P(X^2 + Y^2 \le 10)$.

Answer

npr09_02
Data are in X, Y, P
jcalc
Enter JOINT PROBABILITIES (as on the plane)  P
Enter row matrix of VALUES of X  X
Enter row matrix of VALUES of Y  Y
 Use array operations on matrices X, Y, PX, PY, t, u, and P
M1 = (t+u>=5)|(u<=2);
P1 = total(M1.*P)
P1 =  0.7054
M2 = t.^2 + u.^2 <= 10;
P2 = total(M2.*P)
P2 =  0.3282

Exercise $\PageIndex{8}$

(See Exercsie 7 from "Problems on Random Vectors and Joint Distributions", and Exercise 3 from "Problems on Independent Classes of Random Variables") The pair has the joint distribution

(in m-file npr08_07.m):

$P(X = t, Y =u)$


t =	-3.1	-0.5	1.2	2.4	3.7	4.9
u = 7.5	0.0090	0.0396	0.0594	0.0216	0.0440	0.0203
4.1	0.0495	0	0.1089	0.0528	0.0363	0.0231
-2.0	0.0405	0.1320	0.0891	0.0324	0.0297	0.0189
-3.8	0.0510	0.0484	0.0726	0.0132	0	0.0077

Determine $P(X^2 - 3X \le 0)$, $P(X^3 - 3|Y| < 3)$.

Answer

npr08_07
Data are in X, Y, P
jcalc
Enter JOINT PROBABILITIES (as on the plane)  P
Enter row matrix of VALUES of X  X
Enter row matrix of VALUES of Y  Y
 Use array operations on matrices X, Y, PX, PY, t, u, and P
M1 = t.^2 - 3*t <=0;
P1 = total(M1.*P)
P1 =  0.4500
M2 = t.^3 - 3*abs(u) < 3;
P2 = total(M2.*P)
P2 =  0.7876

Exercise $\PageIndex{9}$

For the pair $\{X, Y\}$ in Exercise 10.4.8, let $Z = g(X, Y) = 3X^2 + 2XY - Y^2$. Determine and plot the distribution function for $Z$.

Answer

G = 3*t.^2 + 2*t.*u - u.^2;  % Determine g(X,Y)
[Z,PZ] = csort(G,P);         % Obtain dbn for Z = g(X,Y)
ddbn                         % Call for plotting m-procedure
Enter row matrix of VALUES  Z
Enter row matrix of PROBABILITIES  PZ   % Plot not reproduced here

Exercise $\PageIndex{10}$

For the pair $\{X, Y\}$ in Exercise 8, let

$W = g(X, Y) = \begin{cases} X & \text{for } X + Y \le 4 \\ 2Y & \text{for } X + Y > 4 \end{cases} = I_M (X, Y) X + I_{M^c} (X, Y) 2Y$

Determine and plot the distribution function for $W$.

Answer

H = t.*(t+u<=4) + 2*u.*(t+u>4);
[W,PW] = csort(H,P);
ddbn
Enter row matrix of VALUES  W
Enter row matrix of PROBABILITIES  PW   % Plot not reproduced here

For the distributions in Exercises 10-15 below

Determine analytically the indicated probabilities.
Use a discrete approximation to calculate the same probablities.'

Exercise $\PageIndex{11}$

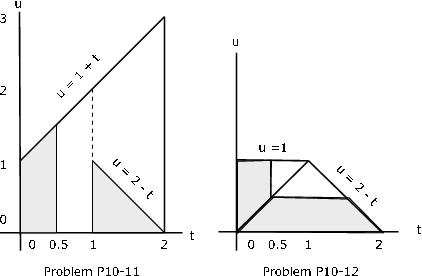
$f_{XY} (t, u) = \dfrac{3}{88} (2t + 3u^2)$ for $0 \le t \le 2$, $0 \le u \le 1+ t$ (see Exercise 15 from "Problems on Random Vectors and Joint Distributions").

$Z = I_{[0, 1]} (X) 4X + I_{(1, 2]} (X) (X + Y)$

Determine $P(Z \le 2)$

Answer

$P(Z \le 2) = P(Z \in Q = Q1M1 \bigvee Q2M2)$, where $M1 = \{(t, u): 0 \le t \le 1, 0 \le u \le 1 + t\}$

$M2 = \{(t, u) : 1 < t \le 2, 0 \le u \le 1 + t\}$

$Q1 = \{(t, u) : 0 \le t \le 1/2\}$, $Q2 = \{(t, u) : u \le 2 - t\}$ (see figure)

$P = \dfrac{3}{88} \int_{0}^{1/2} \int_{0}^{1 + t} (2t + 3u^2) du\ dt + \dfrac{3}{88} \int_{1}^{2} \int_{0}^{2 - t} (2t + 3u^2) du\ dt = \dfrac{563}{5632}$

tuappr
Enter matrix [a b] of X-range endpoints  [0 2]
Enter matrix [c d] of Y-range endpoints  [0 3]
Enter number of X approximation points  200
Enter number of Y approximation points  300
Enter expression for joint density  (3/88)*(2*t + 3*u.^2).*(u<=1+t)
Use array operations on X, Y, PX, PY, t, u, and P
G = 4*t.*(t<=1) + (t+u).*(t>1);
[Z,PZ] = csort(G,P);
PZ2 = (Z<=2)*PZ'
PZ2 =  0.1010                       % Theoretical = 563/5632 = 0.1000

Figure 10.4.1

Exercise $\PageIndex{12}$

$f_{XY} (t, u) = \dfrac{24}{11}$ for $0 \le t \le 2$, $0 \le u \le \text{min } \{1, 2 - t\}$(see Exercise 17 from "Problems on Random Vectors and Joint Distributions").

$Z = I_M(X, Y) \dfrac{1}{2} X + I_{M^c} (X, Y) Y^2$, $M = \{(t, u) : u > t\}$

Determine $P (Z \le 1/4)$.

Answer

$P(Z \le 1/4) = P((X, Y) \in M_1Q_1 \bigvee M_2Q_2)$, $M_1 = \{(t, u): 0 \le t \le u \le 1\}$

$M_2 = \{(t, u) : 0 \le t \le 2, 0 \le t \le \text{min } (t, 2 - t)\}$

$Q_1 = \{(t, u): t \le 1/2\}$ $Q_2 = \{(t, u): u \le 1/2\}$ (see figure)

$P = \dfrac{24}{11} \int_{0}^{1/2} \int_{0}^{1} tu \ du\ dt + \dfrac{24}{11} \int_{1/2}^{3/2} \int_{0}^{1/2} tu\ du\ dt + \dfrac{24}{11} \int_{3/2}^{2} \int_{0}^{2 - t} tu\ du\ dt = \dfrac{85}{176}$

tuappr
Enter matrix [a b] of X-range endpoints  [0 2]
Enter matrix [c d] of Y-range endpoints  [0 1]
Enter number of X approximation points  400
Enter number of Y approximation points  200
Enter expression for joint density  (24/11)*t.*u.*(u<=min(1,2-t))
Use array operations on X, Y, PX, PY, t, u, and P
G = 0.5*t.*(u>t) + u.^2.*(u<t);
[Z,PZ] = csort(G,P);
pp = (Z<=1/4)*PZ'
pp =  0.4844                        % Theoretical = 85/176 = 0.4830

Exercise $\PageIndex{13}$

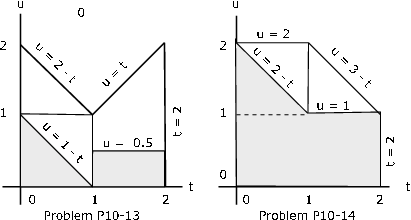
$f_{XY} (t, u) = \dfrac{3}{23} (t + 2u)$ for $0 \le t \le 2$, $0 \le u \le \text{max } \{2 - t, t\}$ (see Exercise 18 from "Problems on Random Vectors and Joint Distributions").

$Z = I_M (X, Y) (X + Y) + I_{M^c} (X, Y)2Y$, $M = \{(t, u): \text{max } (t, u) \le 1\}$

Determine $P(Z \le 1)$

Answer

$P(Z \le 1) = P((X, Y) \in M_1Q_1 \bigvee M_2Q_2)$, $M_1 = \{(t, u): 0 \le t \le 1, 0 \le u \le 1 - t\}$

$M_2 = \{(t, u) : 1 \le t \le 2, 0 \le u \le t\}$

$Q_1 = \{(t, u): u \le 1 - t\}$ $Q_2 = \{(t, u): u \le 1/2\}$ (see figure)

$P = \dfrac{3}{23} \int_{0}^{1} \int_{0}^{1-t} (t + 2u) \ du\ dt + \dfrac{3}{23} \int_{1}^{2} \int_{0}^{1/2} (t + 2u)\ du\ dt = \dfrac{9}{46}$

tuappr
Enter matrix [a b] of X-range endpoints  [0 2]
Enter matrix [c d] of Y-range endpoints  [0 2]
Enter number of X approximation points  300
Enter number of Y approximation points  300
Enter expression for joint density  (3/23)*(t + 2*u).*(u<=max(2-t,t))
Use array operations on X, Y, PX, PY, t, u, and P
M = max(t,u) <= 1;
G = M.*(t + u) + (1 - M)*2.*u;
p = total((G<=1).*P)
p =  0.1960                         % Theoretical = 9/46 = 0.1957

Figure 10.4.2

Exercise $\PageIndex{14}$

$f_{XY} (t, u) = \dfrac{12}{179} (3t^2 + u)$, for $0 \le t \le 2$, $0 \le u \le \text{min } \{2, 3 - t\}$ (see Exercise 19 from "Problems on Random Vectors and Joint Distributions").

$Z = I_M (X, Y) (X + Y) + I_{M^c} (X, Y) 2Y^2$, $M = \{(t, u): t \le 1, u \ge 1\}$

Determine $P(Z \le 2)$.

Answer

$P(Z \le 2) = P((X, Y) \in M_1 Q_1 \bigvee (M_2 \bigvee M_3) Q_2)$, $M_1 = \{(t, u): 0 \le t \le 1, 1 \le u \le 2\}$

$M_2 = \{(t, u) : 0 \le t \le 1, 0 \le u \le 1\}$ $M_3 = \{(t, u): 1 \le t \le 2, 0 \le u \le 3 - t\}$

$Q_1 = \{(t, u): u \le 1 - t\}$ $Q_2 = \{(t, u) : u \le 1/2\}$ (see figure)

$P = \dfrac{12}{179} \int_{0}^{1} \int_{0}^{2 - t} (3t^2 + u) du\ dt + \dfrac{12}{179} \int_{1}^{2} \int_{0}^{1} (3t^2 + u) du\ dt = \dfrac{119}{179}$

tuappr
Enter matrix [a b] of X-range endpoints  [0 2]
Enter matrix [c d] of Y-range endpoints  [0 2]
Enter number of X approximation points  300
Enter number of Y approximation points  300
Enter expression for joint density  (12/179)*(3*t.^2 + u).*(u<=min(2,3-t))
Use array operations on X, Y, PX, PY, t, u, and P
M = (t<=1)&(u>=1);
Z = M.*(t + u) + (1 - M)*2.*u.^2;
G = M.*(t + u) + (1 - M)*2.*u.^2;
p = total((G<=2).*P)
p =  0.6662                          % Theoretical = 119/179 = 0.6648

Exercise $\PageIndex{15}$

$f_{XY} (t, u) = \dfrac{12}{227} (3t + 2tu)$, for $0 \le t \le 2$, $0 \le u \le \text{min } \{1 + t, 2\}$ (see Exercise 20 from "Problems on Random Variables and joint Distributions")

$Z = I_M (X, Y) X + I_{M^c} (X, Y) \dfrac{Y}{X}$, $M = \{(t, u): u \le \text{min } (1, 2 - t)\}$

Determine $P(Z \le 1)$.

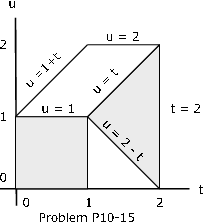
Figure 10.4.3

Answer

$P(Z \le 1) = P((X, Y) \in M_1 Q_1 \bigvee V_2Q_2)$, $M_1 = M$, $M_2 = M^c$

$Q_1 = \{(t, u): 0 \le t \le \}$ $Q_2 = \{(t, u) : u \le t\}$ (see figure)

$P = \dfrac{12}{227} \int_{0}^{1} \int_{0}^{1} (3t + 2tu) du\ dt + \dfrac{12}{227} \int_{1}^{2} \int_{2 - t}^{t} (3t + 2tu) du\ dt = \dfrac{124}{227}$

tuappr
Enter matrix [a b] of X-range endpoints  [0 2]
Enter matrix [c d] of Y-range endpoints  [0 2]
Enter number of X approximation points  400
Enter number of Y approximation points  400
Enter expression for joint density  (12/227)*(3*t+2*t.*u).*(u<=min(1+t,2))
Use array operations on X, Y, PX, PY, t, u, and P
Q = (u<=1).*(t<=1) + (t>1).*(u>=2-t).*(u<=t);
P = total(Q.*P)
P =  0.5478                        % Theoretical = 124/227 = 0.5463

Exercise $\PageIndex{16}$

The class $\{X, Y, Z\}$ is independent.

$X = -2 I_A + I_B + 3I_C$. Minterm probabilities are (in the usual order)

0.255 0.025 0.375 0.045 0.108 0.012 0.162 0.018

$Y = I_D + 3I_E + I_F - 3$. The class $\{D, E, F\}$ is independent with

$P(D) = 0.32$ $P(E) = 0.56$ $P(F) = 0.40$

$Z$ has distribution


Value	-1.3	1.2	2.7	3.4	5.8
Probability	0.12	0.24	0.43	0.13	0.08

Determine $P(X^2 + 3XY^2 >3Z)$.

Answer

% file npr10_16.m  Data for Exercise 16.
cx = [-2 1 3 0];
pmx = 0.001*[255  25 375  45 108  12 162  18];
cy = [1 3 1 -3];
pmy = minprob(0.01*[32 56 40]);
Z = [-1.3 1.2 2.7 3.4 5.8];
PZ = 0.01*[12 24 43 13  8];
disp('Data are in cx, pmx, cy, pmy, Z, PZ')
npr10_16                % Call for data
Data are in cx, pmx, cy, pmy, Z, PZ
[X,PX] = canonicf(cx,pmx);
[Y,PY] = canonicf(cy,pmy);
icalc3
Enter row matrix of X-values  X
Enter row matrix of Y-values  Y
Enter row matrix of Z-values  Z
Enter X probabilities  PX
Enter Y probabilities  PY
Enter Z probabilities  PZ
Use array operations on matrices X, Y, Z,
PX, PY, PZ, t, u, v, and P
M = t.^2 + 3*t.*u.^2 > 3*v;
PM = total(M.*P)
PM =  0.3587

Exercise $\PageIndex{17}$

The simple random variable X has distribution

$X =$ [-3.1 -0.5 1.2 2.4 3.7 4.9] $PX =$ [0.15 0.22 0.33 0.12 0.11 0.07]

Plot the distribution function $F_X$ and the quantile function $Q_X$.
Take a random sample of size $n =$ 10,000. Compare the relative frequency for each value with the probability that value is taken on.

Answer

X = [-3.1 -0.5 1.2 2.4 3.7 4.9];
PX = 0.01*[15 22 33 12 11  7];
ddbn
Enter row matrix of VALUES  X
Enter row matrix of PROBABILITIES  PX  % Plot not reproduced here
dquanplot
Enter VALUES for X  X
Enter PROBABILITIES for X  PX          % Plot not reproduced here
rand('seed',0)                      % Reset random number generator
dsample                             % for comparison purposes
Enter row matrix of VALUES  X
Enter row matrix of PROBABILITIES  PX
Sample size n  10000
    Value      Prob    Rel freq
   -3.1000    0.1500    0.1490
   -0.5000    0.2200    0.2164
    1.2000    0.3300    0.3340
    2.4000    0.1200    0.1184
    3.7000    0.1100    0.1070
    4.9000    0.0700    0.0752
Sample average ex = 0.8792
Population mean E[X] = 0.859
Sample variance vx = 5.146
Population variance Var[X] = 5.112

Search

Text Color

Text Size

Margin Size

Font Type