8.3: Problems on Random Vectors and Joint Distributions
- Page ID
- 10882
Exercise \(\PageIndex{1}\)
Two cards are selected at random, without replacement, from a standard deck. Let \(X\) be the number of aces and \(Y\) be the number of spades. Under the usual assumptions, determine the joint distribution and the marginals.
- Answer
-
Let \(X\) be the number of aces and \(Y\) be the number of spades. Define the events \(AS_i\), \(A_i\), \(S_i\), and \(N_i\), \(i = 1, 2\) of drawing ace of spades, other ace, spade (other than the ace), and neither on the i selection. Let \(P(i, k) = P(X = i, Y = k)\).
\(P(0, 0) = P(N_1N_2) = \dfrac{36}{52} \cdot \dfrac{35}{51} = \dfrac{1260}{2652}\)
\(P(0, 1) = P(N_1S_2 \bigvee S_1N_2) = \dfrac{36}{52} \cdot \dfrac{12}{51} + \dfrac{12}{52} \cdot \dfrac{36}{51} = \dfrac{864}{2652}\)
\(P(0, 2) = P(S_1 S_2) = \dfrac{12}{52} \cdot \dfrac{11}{51} = \dfrac{132}{2652}\)
\(P(1, 0) = P(A_N_2 \bigvee N_1 S_2) = \dfrac{3}{52} \cdot \dfrac{36}{51} + \dfrac{36}{52} \cdot \dfrac{3}{51} = \dfrac{216}{2652}\)
\(P(1, 1) = P(A_1S_2 \bigvee S_1A_2 \bigvee AS_1N_2 \bigvee N_1AS_2) = \dfrac{3}{52} \cdot \dfrac{12}{51} + \dfrac{12}{52} \cdot \dfrac{3}{51} + \dfrac{1}{52} \cdot \dfrac{36}{51} + \dfrac{36}{52} \cdot \dfrac{1}{51} = \dfrac{144}{2652}\)
\(P(1, 2) = P(AS_1S_2 \bigvee S_1AS_2) = \dfrac{1}{52} \cdot \dfrac{12}{51} + \dfrac{12}{52} \cdot \dfrac{1}{51} = \dfrac{24}{2652}\)
\(P(2, 0) = P(A_1A_2) = \dfrac{3}{52} \cdot \dfrac{2}{51} = \dfrac{6}{2652}\)
\(P(2, 1) = P(AS_1A_2 \bigvee A_1AS_2) = \dfrac{1}{52} \cdot \dfrac{3}{51} + \dfrac{3}{52} \cdot \dfrac{1}{51} = \dfrac{6}{2652}\)
\(P(2, 2) = P(\emptyset) = 0\)
% type npr08_01 % file npr08_01.m % Solution for Exercise 8.3.1. X = 0:2; Y = 0:2; Pn = [132 24 0; 864 144 6; 1260 216 6]; P = Pn/(52*51); disp('Data in Pn, P, X, Y') npr08_01 % Call for mfile Data in Pn, P, X, Y % Result PX = sum(P) PX = 0.8507 0.1448 0.0045 PY = fliplr(sum(P')) PY = 0.5588 0.3824 0.0588
Exercise \(\PageIndex{2}\)
Two positions for campus jobs are open. Two sophomores, three juniors, and three seniors apply. It is decided to select two at random (each possible pair equally likely). Let \(X\) be the number of sophomores and \(Y\) be the number of juniors who are selected. Determine the joint distribution for the pair \(\{X, Y\}\) and from this determine the marginals for each.
- Answer
-
Let \(A_i, B_i, C_i\) be the events of selecting a sophomore, junior, or senior, respectively, on the \(i\)th trial. Let \(X\) be the number of sophomores and \(Y\) be the number of juniors selected.
Set \(P(i, k) = P(X = i, Y = k)\)
\(P(0, 0) = P(C_1C_2) = \dfrac{3}{8} \cdot \dfrac{2}{7} = \dfrac{6}{56}\)
\(P(0, 1) = P(B_1C_2) + P(C_1B_2) = \dfrac{3}{8} \cdot \dfrac{3}{7} + \dfrac{3}{8} \cdot \dfrac{3}{7} = \dfrac{18}{56}\)
\(P(0, 2) = P(B_1B_2) = \dfrac{3}{8} \cdot \dfrac{2}{7} = \dfrac{6}{56}\)
\(P(1, 0) = P(A_1C_2) + P(C_1A_2) = \dfrac{2}{8} \cdot \dfrac{3}{7} + \dfrac{3}{8} \cdot \dfrac{2}{7} = \dfrac{12}{56}\)
\(P(1, 1) = P(A_1B_2) + P(B_1A_2) = \dfrac{2}{8} \cdot \dfrac{3}{7} + \dfrac{3}{8} \cdot \dfrac{2}{7} = \dfrac{12}{56}\)
\(P(2, 0) = P(A_1A_2) = \dfrac{2}{8} \cdot \dfrac{1}{7} = \dfrac{2}{56}\)
\(P(1, 2) = P(2, 1) = P(2, 2) = 0\)
\(PX =\) [30/56 24/56 2/56] \(PY =\) [20/56 30/56 6/56]
% file npr08_02.m % Solution for Exercise 8.3.2. X = 0:2; Y = 0:2; Pn = [6 0 0; 18 12 0; 6 12 2]; P = Pn/56; disp('Data are in X, Y,Pn, P') npr08_02 Data are in X, Y,Pn, P PX = sum(P) PX = 0.5357 0.4286 0.0357 PY = fliplr(sum(P')) PY = 0.3571 0.5357 0.1071
Exercise \(\PageIndex{3}\)
A die is rolled. Let \(X\) be the number that turns up. A coin is flipped \(X\) times. Let \(Y\) be the number of heads that turn up. Determine the joint distribution for the pair \(\{X, Y\}\). Assume \(P(X = k) = 1/6\) for \(1 \le k \le 6\) and for each \(k\), \(P(Y = j|X = k)\) has the binomial (\(k\), 1/2) distribution. Arrange the joint matrix as on the plane, with values of \(Y\) increasing upward. Determine the marginal distribution for \(Y\). (For a MATLAB based way to determine the joint distribution see Example 14.1.7 from "Conditional Expectation, Regression")
- Answer
-
\(P(X = i, Y = k) = P(X = i) P(Y = k|X = i) = (1/6) P(Y = k|X = i)\).
% file npr08_03.m % Solution for Exercise 8.3.3. X = 1:6; Y = 0:6; P0 = zeros(6,7); % Initialize for i = 1:6 % Calculate rows of Y probabilities P0(i,1:i+1) = (1/6)*ibinom(i,1/2,0:i); end P = rot90(P0); % Rotate to orient as on the plane PY = fliplr(sum(P')); % Reverse to put in normal order disp('Answers are in X, Y, P, PY') npr08_03 % Call for solution m-file Answers are in X, Y, P, PY disp(P) 0 0 0 0 0 0.0026 0 0 0 0 0.0052 0.0156 0 0 0 0.0104 0.0260 0.0391 0 0 0.0208 0.0417 0.0521 0.0521 0 0.0417 0.0625 0.0625 0.0521 0.0391 0.0833 0.0833 0.0625 0.0417 0.0260 0.0156 0.0833 0.0417 0.0208 0.0104 0.0052 0.0026 disp(PY) 0.1641 0.3125 0.2578 0.1667 0.0755 0.0208 0.0026
Exercise \(\PageIndex{4}\)
As a variation of Exercise 8.3.3., Suppose a pair of dice is rolled instead of a single die. Determine the joint distribution for the pair \(\{X, Y\}\) and from this determine the marginal distribution for \(Y\).
- Answer
-
% file npr08_04.m % Solution for Exercise 8.3.4. X = 2:12; Y = 0:12; PX = (1/36)*[1 2 3 4 5 6 5 4 3 2 1]; P0 = zeros(11,13); for i = 1:11 P0(i,1:i+2) = PX(i)*ibinom(i+1,1/2,0:i+1); end P = rot90(P0); PY = fliplr(sum(P')); disp('Answers are in X, Y, PY, P') npr08_04 Answers are in X, Y, PY, P disp(P) Columns 1 through 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0005 0 0 0 0 0 0.0013 0.0043 0 0 0 0 0.0022 0.0091 0.0152 0 0 0 0.0035 0.0130 0.0273 0.0304 0 0 0.0052 0.0174 0.0326 0.0456 0.0380 0 0.0069 0.0208 0.0347 0.0434 0.0456 0.0304 0.0069 0.0208 0.0312 0.0347 0.0326 0.0273 0.0152 0.0139 0.0208 0.0208 0.0174 0.0130 0.0091 0.0043 0.0069 0.0069 0.0052 0.0035 0.0022 0.0013 0.0005 Columns 8 through 11 0 0 0 0.0000 0 0 0.0000 0.0001 0 0.0001 0.0003 0.0004 0.0002 0.0008 0.0015 0.0015 0.0020 0.0037 0.0045 0.0034 0.0078 0.0098 0.0090 0.0054 0.0182 0.0171 0.0125 0.0063 0.0273 0.0205 0.0125 0.0054 0.0273 0.0171 0.0090 0.0034 0.0182 0.0098 0.0045 0.0015 0.0078 0.0037 0.0015 0.0004 0.0020 0.0008 0.0003 0.0001 0.0002 0.0001 0.0000 0.0000 disp(PY) Columns 1 through 7 0.0269 0.1025 0.1823 0.2158 0.1954 0.1400 0.0806 Columns 8 through 13 0.0375 0.0140 0.0040 0.0008 0.0001 0.0000
Exercise \(\PageIndex{5}\)
Suppose a pair of dice is rolled. Let \(X\) be the total number of spots which turn up. Roll the pair an additional \(X\) times. Let \(Y\) be the number of sevens that are thrown on the \(X\) rolls. Determine the joint distribution for the pair \(\{X, Y\}\) and from this determine the marginal distribution for \(Y\). What is the probability of three or more sevens?
- Answer
-
% file npr08_05.m % Data and basic calculations for Exercise 8.3.5. PX = (1/36)*[1 2 3 4 5 6 5 4 3 2 1]; X = 2:12; Y = 0:12; P0 = zeros(11,13); for i = 1:11 P0(i,1:i+2) = PX(i)*ibinom(i+1,1/6,0:i+1); end P = rot90(P0); PY = fliplr(sum(P')); disp('Answers are in X, Y, P, PY') npr08_05 Answers are in X, Y, P, PY disp(PY) Columns 1 through 7 0.3072 0.3660 0.2152 0.0828 0.0230 0.0048 0.0008 Columns 8 through 13 0.0001 0.0000 0.0000 0.0000 0.0000 0.0000
Exercise \(\PageIndex{6}\)
The pair \(\{X, Y\}\) has the joint distribution (in m-file npr08_06.m):
\(X =\) [-2.3 -0.7 1.1 3.9 5.1] \(Y =\) = [1.3 2.5 4.1 5.3]
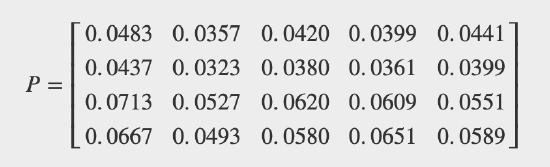
Determine the marginal distribution and the corner values for \(F_{XY}\). Determine \(P(X + Y > 2)\) and \(P(X \ge Y)\).
- Answer
-
npr08_06 Data are in X, Y, P jcalc Enter JOINT PROBABILITIES (as on the plane) P Enter row matrix of VALUES of X X Enter row matrix of VALUES of Y Y Use array operations on matrices X, Y, PX, PY, t, u, and P disp([X;PX]') -2.3000 0.2300 -0.7000 0.1700 1.1000 0.2000 3.9000 0.2020 5.1000 0.1980 disp([Y;PY]') 1.3000 0.2980 2.5000 0.3020 4.1000 0.1900 5.3000 0.2100 jddbn Enter joint probability matrix (as on the plane) P To view joint distribution function, call for FXY disp(FXY) 0.2300 0.4000 0.6000 0.8020 1.0000 0.1817 0.3160 0.4740 0.6361 0.7900 0.1380 0.2400 0.3600 0.4860 0.6000 0.0667 0.1160 0.1740 0.2391 0.2980 P1 = total((t+u>2).*P) P1 = 0.7163 P2 = total((t>=u).*P) P2 = 0.2799
Exercise \(\PageIndex{7}\)
The pair \(\{X, Y\}\) has the joint distribution (in m-file npr08_07.m):
\(P(X = i, Y = u)\)
| t = | -3.1 | -0.5 | 1.2 | 2.4 | 3.7 | 4.9 |
| u = 7.5 | 0.0090 | 0.0396 | 0.0594 | 0.0216 | 0.0440 | 0.0203 |
| 4.1 | 0.0495 | 0 | 0.1089 | 0.0528 | 0.0363 | 0.0231 |
| -2.0 | 0.0405 | 0.1320 | 0.0891 | 0.0324 | 0.0297 | 0.0189 |
| -3.8 | 0.0510 | 0.0484 | 0.0726 | 0.0132 | 0 | 0.0077 |
Determine the marginal distributions and the corner values for \(F_{XY}\). Determine \(P(1 \le X \le 4, Y > 4)\) and \(P(|X - Y| \le 2)\).
- Answer
-
npr08_07 Data are in X, Y, P jcalc Enter JOINT PROBABILITIES (as on the plane) P Enter row matrix of VALUES of X X Enter row matrix of VALUES of Y Y Use array operations on matrices X, Y, PX, PY, t, u, and P disp([X;PX]') -3.1000 0.1500 -0.5000 0.2200 1.2000 0.3300 2.4000 0.1200 3.7000 0.1100 4.9000 0.0700 disp([Y;PY]') -3.8000 0.1929 -2.0000 0.3426 4.1000 0.2706 7.5000 0.1939 jddbn Enter joint probability matrix (as on the plane) P To view joint distribution function, call for FXY disp(FXY) 0.1500 0.3700 0.7000 0.8200 0.9300 1.0000 0.1410 0.3214 0.5920 0.6904 0.7564 0.8061 0.0915 0.2719 0.4336 0.4792 0.5089 0.5355 0.0510 0.0994 0.1720 0.1852 0.1852 0.1929 M = (1<=t)&(t<=4)&(u>4); P1 = total(M.*P) P1 = 0.3230 P2 = total((abs(t-u)<=2).*P) P2 = 0.3357
Exercise \(\PageIndex{8}\)
The pair \(\{X, Y\}\) has the joint distribution (in m-file npr08_08.m):
\(P(X = t, Y = u)\)
| t = | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 |
| u = 12 | 0.0156 | 0.0191 | 0.0081 | 0.0035 | 0.0091 | 0.0070 | 0.0098 | 0.0056 | 0.0091 | 0.0049 |
| 10 | 0.0064 | 0.0204 | 0.0108 | 0.0040 | 0.0054 | 0.0080 | 0.0112 | 0.0064 | 0.0104 | 0.0056 |
| 9 | 0.0196 | 0.0256 | 0.0126 | 0.0060 | 0.0156 | 0.0120 | 0.0168 | 0.0096 | 0.0056 | 0.0084 |
| 5 | 0.0112 | 0.0182 | 0.0108 | 0.0070 | 0.0182 | 0.0140 | 0.0196 | 0.0012 | 0.0182 | 0.0038 |
| 3 | 0.0060 | 0.0260 | 0.0162 | 0.0050 | 0.0160 | 0.0200 | 0.0280 | 0.0060 | 0.0160 | 0.0040 |
| -1 | 0.0096 | 0.0056 | 0.0072 | 0.0060 | 0.0256 | 0.0120 | 0.0268 | 0.0096 | 0.0256 | 0.0084 |
| -3 | 0.0044 | 0.0134 | 0.0180 | 0.0140 | 0.0234 | 0.0180 | 0.0252 | 0.0244 | 0.0234 | 0.0126 |
| -5 | 0.0072 | 0.0017 | 0.0063 | 0.0045 | 0.0167 | 0.0090 | 0.0026 | 0.0172 | 0.0217 | 0.0223 |
Determine the marginal distributions. Determine \(F_{XY} (10, 6)\) and \(P(X > Y)\).
- Answer
-
npr08_08 Data are in X, Y, P jcalc - - - - - - - - - Use array operations on matrices X, Y, PX, PY, t, u, and P disp([X;PX]') 1.0000 0.0800 3.0000 0.1300 5.0000 0.0900 7.0000 0.0500 9.0000 0.1300 11.0000 0.1000 13.0000 0.1400 15.0000 0.0800 17.0000 0.1300 19.0000 0.0700 disp([Y;PY]') -5.0000 0.1092 -3.0000 0.1768 -1.0000 0.1364 3.0000 0.1432 5.0000 0.1222 9.0000 0.1318 10.0000 0.0886 12.0000 0.0918 F = total(((t<=10)&(u<=6)).*P) F = 0.2982 P = total((t>u).*P) P = 0.7390
Exercise \(\PageIndex{9}\)
Data were kept on the effect of training time on the time to perform a job on a production line. \(X\) is the amount of training, in hours, and \(Y\) is the time to perform the task, in minutes. The data are as follows (in m-file npr08_09.m):
\(P(X = t, Y = u)\)
| t = | 1 | 1.5 | 2 | 2.5 | 3 |
| u = 5 | 0.039 | 0.011 | 0.005 | 0.001 | 0.001 |
| 4 | 0.065 | 0.070 | 0.050 | 0.015 | 0.010 |
| 3 | 0.031 | 0.061 | 0.137 | 0.051 | 0.033 |
| 2 | 0.012 | 0.049 | 0.163 | 0.058 | 0.039 |
| 1 | 0.003 | 0.009 | 0.045 | 0.025 | 0.017 |
Determine the marginal distributions. Determine \(F_{XY}(2, 3)\) and \(P(Y/X \ge 1.25)\).
- Answer
-
npr08_09 Data are in X, Y, P jcalc - - - - - - - - - - - - Use array operations on matrices X, Y, PX, PY, t, u, and P disp([X;PX]') 1.0000 0.1500 1.5000 0.2000 2.0000 0.4000 2.5000 0.1500 3.0000 0.1000 disp([Y;PY]') 1.0000 0.0990 2.0000 0.3210 3.0000 0.3130 4.0000 0.2100 5.0000 0.0570 F = total(((t<=2)&(u<=3)).*P) F = 0.5100 P = total((u./t>=1.25).*P) P = 0.5570
For the joint densities in Exercises 10-22 below
- Sketch the region of definition and determine analytically the marginal density functions \(f_X\) and \(f_Y\).
- Use a discrete approximation to plot the marginal density \(f_X\) and the marginal distribution function \(F_X\).
- Calculate analytically the indicated probabilities.
- Determine by discrete approximation the indicated probabilities.
Exercise \(\PageIndex{10}\)
\(f_{XY}(t, u) = 1\) for \(0 \le t \le 1\), \(0 \le u \le 2(1 - t)\).
\(P(X > 1/2, Y > 1), P(0 \le X \le 1/2, Y > 1/2), P(Y \le X)\)
- Answer
-
Region is triangle with vertices (0, 0), (1, 0), (0, 2).
\(f_{X} (t) = \int_{0}^{2(1-t)} du = 2(1 - t)\), \(0 \le t \le 1\)
\(f_{Y} (u) = \int_{0}^{1 - u/2} dt = 1 - u/2\), \(0 \le u \le 2\)
\(M1 = \{(t, u):t > 1/2, u> 1\}\) lies outside the trianlge \(P((X, Y) \in M1) = 0\)
\(M2 = \{(t, u): 0 \le t \le 1/2, u > 1/2\}\) has area in the triangle = 1/2
\(M3\) = the region in the triangle under \(u = t\), which has area 1/3
tuappr Enter matrix [a b] of X-range endpoints [0 1] Enter matrix [c d] of Y-range endpoints [0 2] Enter number of X approximation points 200 Enter number of Y approximation points 400 Enter expression for joint density (t<=1)&(u<=2*(1-t)) Use array operations on X, Y, PX, PY, t, u, and P fx = PX/dx; FX = cumsum(PX); plot(X,fx,X,FX) % Figure not reproduced M1 = (t>0.5)&(u>1); P1 = total(M1.*P) P1 = 0 % Theoretical = 0 M2 = (t<=0.5)&(u>0.5); P2 = total(M2.*P) P2 = 0.5000 % Theoretical = 1/2 P3 = total((u<=t).*P) P3 = 0.3350 % Theoretical = 1/3
Exercise \(\PageIndex{11}\)
\(f_{XY} (t, u) = 1/2\) on the square with vertices at (1, 0), (2, 1), (1, 2), (0, 1).
\(P(X > 1, Y > 1), P(X \le 1/2, 1 < Y), P(Y \le X)\)
- Answer
-
The region is bounded by lines \(u = 1 + t\), \( u = 1 - t\), \(u = 3 - t\), and \(u = t - 1\)
\(f_X (t) = I_{[0,1]} (t) 0.5 \int_{1 - t}^{1 + t} du + I_{(1, 2]} (t) 0.5 \int_{t - 1}^{3 - t} du = I_{(1, 2]} (t) (2 - t) = f_Y(t)\) by symmetry
\(M1 = \{(t, u): t > 1, u > 1\}\) has area in the trangle = 1/2, so \(PM1 = 1/4\)
\(M2 = \{(t, u): t \le 1/2, u > 1\}\) has area in the trangle = 1/8\), so \(PM2 = 1/16\)
\(M3 = \{(t, u): u \le t\}\) has area in the trangle = 1, so \(PM3 = 1/2\)
tuappr Enter matrix [a b] of X-range endpoints [0 2] Enter matrix [c d] of Y-range endpoints [0 2] Enter number of X approximation points 200 Enter number of Y approximation points 200 Enter expression for joint density 0.5*(u<=min(1+t,3-t))& ... (u>=max(1-t,t-1)) Use array operations on X, Y, PX, PY, t, u, and P fx = PX/dx; FX = cumsum(PX); plot(X,fx,X,FX) % Plot not shown M1 = (t>1)&(u>1); PM1 = total(M1.*P) PM1 = 0.2501 % Theoretical = 1/4 M2 = (t<=1/2)&(u>1); PM2 = total(M2.*P) PM2 = 0.0631 % Theoretical = 1/16 = 0.0625 M3 = u<=t; PM3 = total(M3.*P) PM3 = 0.5023 % Theoretical = 1/2
Exercise \(\PageIndex{12}\)
\(f_{XY} (t, u) = 4t(1 - u)\) for \(0 \le t \le 1\), \(0 \le u \le 1\).
\(P(1/2 < X < 3/4, Y > 1/2)\), \(P(X \le 1/2, Y > 1/2)\), \(P(Y \le X)\)
- Answer
-
Region is the unit square,
\(f_X (t) = \int_{0}^{1} 4t(1 - u) du = 2t\), \(0 \le t \le 1\)
\(f_Y(u) = \int_{0}^{1} 4t(1 - u) dt = 2(1 - u)\), \(0 \le u \le 1\)
\(P1 = \int_{1/2}^{3/4} \int_{1/2}^{1} 4t (1 - u) du dt = 5/64\) \(P2 = \int_{0}^{1/2} \int_{1/2}^{1} 4t(1 - u) dudt = 1/16\)
\(P3 = \int_{0}^{1} \int_{0}^{t} 4t(1 - u) du dt = 5/6\)
tuappr Enter matrix [a b] of X-range endpoints [0 1] Enter matrix [c d] of Y-range endpoints [0 1] Enter number of X approximation points 200 Enter number of Y approximation points 200 Enter expression for joint density 4*t.*(1 - u) Use array operations on X, Y, PX, PY, t, u, and P fx = PX/dx; FX = cumsum(PX); plot(X,fx,X,FX) % Plot not shown M1 = (1/2<t)&(t<3/4)&(u>1/2); P1 = total(M1.*P) P1 = 0.0781 % Theoretical = 5/64 = 0.0781 M2 = (t<=1/2)&(u>1/2); P2 = total(M2.*P) P2 = 0.0625 % Theoretical = 1/16 = 0.0625 M3 = (u<=t); P3 = total(M3.*P) P3 = 0.8350 % Theoretical = 5/6 = 0.8333
Exercise \(\PageIndex{13}\)
\(f_{XY} (t, u) = \dfrac{1}{8} (t + u)\) for \(0 \le t \le 2\), \(0 \le u \le 2\).
\(P(X > 1/2, Y > 1/2), P(0 \le X \le 1, Y > 1), P(Y \le X)\)
- Answer
-
Region is the square \(0 \le t \le 2\), \(0 \le u \le 2\)
\(f_X (t) = \dfrac{1}{8} \int_{0}^{2} (t + u) = \dfrac{1}{4} ( t + 1) = f_Y(t)\), \(0 \le t \le 2\)
\(P1 = \int_{1/2}^{2} \int_{1/2}^{2} (t + u) dudt = 45/64\) \(P2 = \int_{0}^{1} \int_{1}^{2} (t + u) du dt = 1/4\)
\(P3 = \int_{0}^{2} \int_{0}^{1} (t + u) dudt = 1/2\)
tuappr Enter matrix [a b] of X-range endpoints [0 2] Enter matrix [c d] of Y-range endpoints [0 2] Enter number of X approximation points 200 Enter number of Y approximation points 200 Enter expression for joint density (1/8)*(t+u) Use array operations on X, Y, PX, PY, t, u, and P fx = PX/dx; FX = cumsum(PX); plot(X,fx,X,FX) M1 = (t>1/2)&(u>1/2); P1 = total(M1.*P) P1 = 0.7031 % Theoretical = 45/64 = 0.7031 M2 = (t<=1)&(u>1); P2 = total(M2.*P) P2 = 0.2500 % Theoretical = 1/4 M3 = u<=t; P3 = total(M3.*P) P3 = 0.5025 % Theoretical = 1/2
Exercise \(\PageIndex{14}\)
\(f_{XY}(t, u) = 4ue^{-2t}\) for \(0 \le t, 0 \le u \le 1\)
\(P(X \le 1, Y > 1), P(X > 0, 1/2 < Y < 3/4), P(X < Y)\)
- Answer
-
Region is strip by \(t = 0, u = 0, u = 1\)
\(f_X(t) = 2e^{-2t}\), \(0 \le t\), \(f_Y(u) = 2u\), \(0 \le u \le 1\), \(f_{XY} = f_X f_Y\)
\(P1 = 0\), \(P2 = \int_{0.5}^{\infty} 2e^{-2t} dt \int_{1/2}^{3/4} 2udu = e^{-1} 5/16\)
\(P3 = 4 \int_{0}^{1} \int_{t}^{1} ue^{-2t} dudt = \dfrac{3}{2} e^{-2} + \dfrac{1}{2} = 0.7030\)
tuappr Enter matrix [a b] of X-range endpoints [0 3] Enter matrix [c d] of Y-range endpoints [0 1] Enter number of X approximation points 400 Enter number of Y approximation points 200 Enter expression for joint density 4*u.*exp(-2*t) Use array operations on X, Y, PX, PY, t, u, and P M2 = (t > 0.5)&(u > 0.5)&(u<3/4); p2 = total(M2.*P) p2 = 0.1139 % Theoretical = (5/16)exp(-1) = 0.1150 p3 = total((t<u).*P) p3 = 0.7047 % Theoretical = 0.7030
Exercise \(\PageIndex{15}\)
\(f_{XY} (t, u) = \dfrac{3}{88} (2t + 3u^2)\) for \(0 \le t \le 2\), \(0 \le u \le 1 + t\).
\(F_{XY} (1, 1)\), \(P(X \le 1, Y > 1)\), \(P(|X - Y| < 1)\)
- Answer
-
Region bounded by \(t = 0\), \(t = 2\), \(u = 0\), \(u = 1 + t\)
\(f_X (t) = \dfrac{3}{88} \int_{0}^{1 + t} (2t + 3u^2) du = \dfrac{3}{88}(1 + t)(1 + 4t + t^2) = \dfrac{3}{88} ( 1 + 5t + 5t^2 + t^3)\), \(0 \le t \le 2\)
\(f_Y(u) = I_{[0,1]} (u) \dfrac{3}{88} \int_{0}^{2} (2t + 3u^2) dt + I_{(1, 3]} (u) \dfrac{3}{88} \int_{u - 1}^{2} (2t + 3u^2) dt = \)
\(I_{[0,1]} (u) \dfrac{3}{88} (6u^2 + 4) + I_{(1,3]} (t) \dfrac{3}{88} (3 + 2u + 8u^2 - 3u^3)\)
\(F_{XY}(1, 1) = \int_{0}^{1} \int_{0}^{1} f_{XY} (t, u) dudt = 3/44\)
\(P1 = \int_{0}^{1} \int_{1}^{1 + t} f_{XY} (t, u)dudt = 41/352\) \(P2 = \int_{0}^{1} \int_{1}^{1 + t} f_{XY} (t, u) dudt = 329/352\)
tuappr Enter matrix [a b] of X-range endpoints [0 2] Enter matrix [c d] of Y-range endpoints [0 3] Enter number of X approximation points 200 Enter number of Y approximation points 300 Enter expression for joint density (3/88)*(2*t+3*u.^2).*(u<=1+t) Use array operations on X, Y, PX, PY, t, u, and P fx = PX/dx; FX = cumsum(PX); plot(X,fx,X,FX) MF = (t<=1)&(u<=1); F = total(MF.*P) F = 0.0681 % Theoretical = 3/44 = 0.0682 M1 = (t<=1)&(u>1); P1 = total(M1.*P) P1 = 0.1172 % Theoretical = 41/352 = 0.1165 M2 = abs(t-u)<1; P2 = total(M2.*P) P2 = 0.9297 % Theoretical = 329/352 = 0.9347
Exercise \(\PageIndex{16}\)
\(f_{XY} (t, u) = 12t^2u\) on the parallelogram with vertices (-1, 0), (0, 0), (1, 1), (0, 1).
\(P(X \le 1/2, Y > 0), P(X < 1/2, Y \le 1/2), P(Y \ge 1/2)\)
- Answer
-
Region bounded by \(u = 0\), \(u = t\), \(u = 1\), \(u = t + 1\)
\(f_X (t) = I_{[-1, 0]} (t) 12 \int_{0}^{t + 1} t^2 u du + I_{(0, 1]} (t) 12 \int_{t}^{1} t^2 u du = I_{[-1, 0]} (t) 6t^2 (t + 1)^2 + I_{(0, 1]}(t) 6t^2(1 - t^2)\)
\(f_Y(u) = 12\int_{u - 1}^{t} t^2 udu + 12u^3 - 12u^2 + 4u\), \(0 \le u \le 1\)
\(P1 = 1 - 12 \int_{1/2}^{1} \int_{t}^{1} t^2 ududt = 33/80\), \(P2 = 12 \int_{0}^{1/2} \int_{u - 1}^{u} t^2 udtdu = 3/16\)
\(P3 = 1 - P2 = 13/16\)
tuappr Enter matrix [a b] of X-range endpoints [-1 1] Enter matrix [c d] of Y-range endpoints [0 1] Enter number of X approximation points 400 Enter number of Y approximation points 200 Enter expression for joint density 12*u.*t.^2.*((u<=t+1)&(u>=t)) Use array operations on X, Y, PX, PY, t, u, and P p1 = total((t<=1/2).*P) p1 = 0.4098 % Theoretical = 33/80 = 0.4125 M2 = (t<1/2)&(u<=1/2); p2 = total(M2.*P) p2 = 0.1856 % Theoretical = 3/16 = 0.1875 P3 = total((u>=1/2).*P) P3 = 0.8144 % Theoretical = 13/16 = 0.8125
Exercise \(\PageIndex{17}\)
\(f_{XY} (t, u) = \dfrac{24}{11} tu\) for \(0 \le t \le 2\), \(0 \le u \le \text{min}\ \{1, 2 - t\}\)
\(P(X \le 1, Y \le 1), P(X > 1), P(X < Y)\)
- Answer
-
Region is bounded by \(t = 0, u = 0, u = 2, u = 2 - t\)
\(f_X (t) = I_{[0, 1]} (t) \dfrac{24}{11} \int_{0}^{1} tudu + I_{(1, 2]} (t) \dfrac{24}{11} \int_{0}^{2 - t} tudu =\)
\(I_{[0, 1]} (t) \dfrac{12}{11} t + I_{(1, 2]} (t) \dfrac{12}{11} t(2 - t)^2\)
\(f_Y (u) = \dfrac{24}{11} \int_{0}^{2 - u} tudt = \dfrac{12}{11} u(u - 2)^2\), \(0 \le u \le 1\)
\(P1 = \dfrac{24}{11} \int_{0}^{1} \int_{0}^{1} tududt = 6/11\) \(P2 = \dfrac{24}{11} \int_{1}^{2} \int_{0}^{2 - t} tududt = 5/11\)
\(P3 = \dfrac{24}{11} \int_{0}^{1} \int_{t}^{1} tududt = 3/11\)
tuappr Enter matrix [a b] of X-range endpoints [0 2] Enter matrix [c d] of Y-range endpoints [0 1] Enter number of X approximation points 400 Enter number of Y approximation points 200 Enter expression for joint density (24/11)*t.*u.*(u<=2-t) Use array operations on X, Y, PX, PY, t, u, and P M1 = (t<=1)&(u<=1); P1 = total(M1.*P) P1 = 0.5447 % Theoretical = 6/11 = 0.5455 P2 = total((t>1).*P) P2 = 0.4553 % Theoretical = 5/11 = 0.4545 P3 = total((t<u).*P) P3 = 0.2705 % Theoretical = 3/11 = 0.2727
Exercise \(\PageIndex{18}\)
\(f_{XY} (t, u) = \dfrac{3}{23} (t + 2u)\) for \(0 \le t \le 2\), \(0 \le u \le \text{max}\ \{2 - t, t\}\)
\(P(X \ge 1, Y \ge 1), P(Y \le 1), P(Y \le X)\)
- Answer
-
Region is bounded by \(t = 0, t = 2, u = 0, u = 2 - t\) \((0 \le t \le 1)\), \(u = t (1 < t \le 2)\)
\(f_X(t) = I_{[0,1]} (t) \dfrac{3}{23} \int_{0}^{2 - t} (t + 2u) du + I_{(1, 2]} (t) \dfrac{3}{23} \int_{0}^{t} (t + 2u) du = I_{[0, 1]} (t) \dfrac{6}{23} (2 - t) + I_{(1, 2]} (t) \dfrac{6}{23}t^2\)
\(f_Y(u) = I_{[0, 1]} (u) \dfrac{3}{23} \int_{0}^{2} (t + 2u) du + I_{(1, 2]} (u) [\dfrac{3}{23} \int_{0}^{2 - u} (t + 2u) dt + \dfrac{3}{23} \int_{u}^{2} (t + 2u) dt]=\)
\(I_{[0,1]} (u) \dfrac{6}{23} (2u + 1) + I_{(1, 2]} (u) \dfrac{3}{23} (4 + 6u - 4u^2)\)
\(P1 = \dfrac{3}{23} \int_{1}^{2} \int_{1}^{t} (t + 2u) du dt = 13/46\), \(P2 = \dfrac{3}{23} \int_{0}^{2} \int_{0}^{1} (t + 2u) du dt = 12/23\)
\(P3 = \dfrac{3}{23} \int_{0}^{2} \int_{0}^{t} (t + 2u) dudt = 16/23\)
tuappr Enter matrix [a b] of X-range endpoints [0 2] Enter matrix [c d] of Y-range endpoints [0 2] Enter number of X approximation points 200 Enter number of Y approximation points 200 Enter expression for joint density (3/23)*(t+2*u).*(u<=max(2-t,t)) Use array operations on X, Y, PX, PY, t, u, and P M1 = (t>=1)&(u>=1); P1 = total(M1.*P) P1 = 0.2841 13/46 % Theoretical = 13/46 = 0.2826 P2 = total((u<=1).*P) P2 = 0.5190 % Theoretical = 12/23 = 0.5217 P3 = total((u<=t).*P) P3 = 0.6959 % Theoretical = 16/23 = 0.6957
Exercise \(\PageIndex{19}\)
\(f_{XY} (t, u) = \dfrac{12}{179} (3t^2 + u)\), for \(0 \le t \le 2\), \(0 \le u \le \text{min } \{1 + t, 2\}\)
\(P(X \ge 1, Y \ge 1), P(X \le 1, Y \le 1), P(Y < X)\)
- Answer
-
Region has two parts: (1) \(0 \le t \le 1, 0 \le u \le 2\) (2) \(1 < t \le 2, 0 \le u \le 3 - t\)
\(f_X (t) = I_{[0, 1]} (t) \dfrac{12}{179} \int_{0}^{2} (3t^2 + u) du + I_{(1, 2]} (t) \dfrac{12}{179} \int_{0}^{3 - t} (3t^2 + u) du =\)
\(I_{[0, 1]} (t) \dfrac{24}{179} (3t^2 + 1) + I_{(1, 2]} (t) \dfrac{6}{179} (9 - 6t + 19t^2 - 6t^3)\)
\(f_Y(u) = I_{[0, 1]} (u) \dfrac{12}{179} \int_{0}^{2}(3t^2 + u) dt + I_{(1, 2]} (u) \dfrac{12}{179} \int_{0}^{3 - u} (3t^2 + u) dt =\)
\(I_{[0, 1]} (u) \dfrac{24}{179} (4 + u) + I_{(1, 2]} (u) \dfrac{12}{179} (27 - 24u + 8u^2 - u^3)\)
\(P1 = \dfrac{12}{179} \int{1}^{2} \int_{1}^{3 - t} (3t^2 + u) du dt = 41/179\) \(P2 = \dfrac{12}{179} \int_{0}^{1} \int_{0}^{1} (3t^2 + u) dudt = 18/179\)
\(P3 = \dfrac{12}{179} \int_{0}^{3/2} \int_{0}^{t} (3t^2 + u) dudt + \dfrac{12}{179} \int_{3/2}^{2} \int_{0}^{3 - t} (3t^2 + u) dudt = 1001/1432\)
tuappr Enter matrix [a b] of X-range endpoints [0 2] Enter matrix [c d] of Y-range endpoints [0 2] Enter number of X approximation points 200 Enter number of Y approximation points 200 Enter expression for joint density (12/179)*(3*t.^2+u).* ... (u<=min(2,3-t)) Use array operations on X, Y, PX, PY, t, u, and P fx = PX/dx; FX = cumsum(PX); plot(X,fx,X,FX) M1 = (t>=1)&(u>=1); P1 = total(M1.*P) P1 = 2312 % Theoretical = 41/179 = 0.2291 M2 = (t<=1)&(u<=1); P2 = total(M2.*P) P2 = 0.1003 % Theoretical = 18/179 = 0.1006 M3 = u<=min(t,3-t); P3 = total(M3.*P) P3 = 0.7003 % Theoretical = 1001/1432 = 0.6990
Exercise \(\PageIndex{20}\)
\(f_{XY} (t, u) = \dfrac{12}{227} (3t + 2tu)\) for \(0 \le t \le 2\), \(0 \le u \le \text{min} \{1 + t, 2\}\)
\(P(X \le 1/2, Y \le 3/2), P(X \le 1.5, Y > 1), P(Y < X)\)
- Answer
-
Region is in two parts:
- \(0 \le t \le 1\), \(0 \le u \le 1 + t\)
- \(1 < t \le 2\), \(0 \le u \le 2\)
\(f_X(t) = I_{[0,1]} (t) \int_{0}^{1+t} f_{XY} (t, u) du + I_{(1, 2]} (t) \int_{0}^{2} f_{XY} (t, u) du =\)
\(I_{[0, 1]} (t) \dfrac{12}{227} (t^3 + 5t^2 + 4t) + I_{(1, 2]} (t) \dfrac{120}{227} t\)
\(f_Y(u) = I_{[0, 1]} (u) \int_{0}^{2} f_{XY} (t, u) dt + I_{(1, 2]} (u) \int_{u - 1}^{2} f_{XY} (t, u) dt = \)
\(I_{[0, 1]} (u) \dfrac{24}{227} (2u + 3) + I_{(1, 2]} (u) \dfrac{6}{227} (2u + 3) (3 + 2u - u^2)\)
\(= I_{[0, 1]} (u) \dfrac{24}{227} (2u + 3) + I_{(1, 2]} (u) \dfrac{6}{227} (9 + 12 u + u^2 - 2u^3)\)
\(P1 = \dfrac{12}{227} \int_{0}^{1/2} \int_{0}^{1 + t} (3t + 2tu) du dt = 139/3632\)
\(P2 = \dfrac{12}{227} \int_{0}^{1} \int_{1}^{1 + t} (3t + 2tu) dudt + \dfrac{12}{227} \int_{1}^{3/2} \int_{1}^{2} (3t + 2tu) du dt = 68/227\)
\(P3 = \dfrac{12}{227} \int_{0}^{2} \int_{1}^{t} (3t + 2tu) dudt = 144/227\)
tuappr Enter matrix [a b] of X-range endpoints [0 2] Enter matrix [c d] of Y-range endpoints [0 2] Enter number of X approximation points 200 Enter number of Y approximation points 200 Enter expression for joint density (12/227)*(3*t+2*t.*u).* ... (u<=min(1+t,2)) Use array operations on X, Y, PX, PY, t, u, and P M1 = (t<=1/2)&(u<=3/2); P1 = total(M1.*P) P1 = 0.0384 % Theoretical = 139/3632 = 0.0383 M2 = (t<=3/2)&(u>1); P2 = total(M2.*P) P2 = 0.3001 % Theoretical = 68/227 = 0.2996 M3 = u<t; P3 = total(M3.*P) P3 = 0.6308 % Theoretical = 144/227 = 0.6344
Exercise \(\PageIndex{21}\)
\(f_{XY} (t, u) = \dfrac{2}{13} (t + 2u)\) for \(0 \le t \le 2\), \(0 \le u \le \text{min}\ \{2t, 3 - t\}\)
\(P(X < 1), P(X \ge 1, Y \le 1), P(Y \le X/2)\)
- Answer
-
Region bounded by \(t = 2, u = 2t\) \((0 \le t \le 1)\), \(3 - t\) \((1 \le t \le 2)\)
\(f_X(t) = I_{[0, 1]} (t) \dfrac{2}{13} \int_{0}^{2t} (t + 2u) du + I_{(1, 2]} (t) \dfrac{2}{13} \int_{0}^{3 - t} (t + 2u) du = I_{[0, 1]} (t) \dfrac{12}{13} t^2 + I_{(1, 2]} (t) \dfrac{6}{13} (3 - t)\)
\(f_Y (u) = I_{[0, 1]} (u) \dfrac{2}{13} \int_{u/2}^{2} (t + 2u) dt + I_{(1, 2]} (u) \dfrac{2}{13} \int_{u/2}^{3 - u} (t + 2u) dt =\)
\(I_{[0, 1]} (u) (\dfrac{4}{13} + \dfrac{8}{13}u - \dfrac{9}{52} u^2) + I_{(1, 2]} (u) (\dfrac{9}{13} + \dfrac{6}{13} u - \dfrac{21}{52} u^2)\)
\(P1 = \int_{0}^{1} \int_{0}^{2t} (t + 2u) dudt = 4/13\) \(P2 = \int_{1}^{2} \int_{0}^{1} (t + 2u)dudt = 5/13\)
\(P3 = \int_{0}^{2} \int_{0}^{u/2} (t + 2u) dudt = 4/13\)
tuappr Enter matrix [a b] of X-range endpoints [0 2] Enter matrix [c d] of Y-range endpoints [0 2] Enter number of X approximation points 400 Enter number of Y approximation points 400 Enter expression for joint density (2/13)*(t+2*u).*(u<=min(2*t,3-t)) Use array operations on X, Y, PX, PY, t, u, and P P1 = total((t<1).*P) P1 = 0.3076 % Theoretical = 4/13 = 0.3077 M2 = (t>=1)&(u<=1); P2 = total(M2.*P) P2 = 0.3844 % Theoretical = 5/13 = 0.3846 P3 = total((u<=t/2).*P) P3 = 0.3076 % Theoretical = 4/13 = 0.3077
Exercise \(\PageIndex{22}\)
\(f_{XY} (t, u) = I_{[0, 1]} (t) \dfrac{3}{8} (t^2 + 2u) + I_{(1, 2]} (t) \dfrac{9}{14} t^2u^2\) for \(0 \le u \le 1\).
\(P(1/2 \le X \le 3/2, Y \le 1/2)\)
- Answer
-
Region is rectangle bounded by \(t = 0\), \(t = 2\), \(u = 0\), \(u = 1\)
\(f_{XY} (t, u) = I_{[0, 1]} (t) \dfrac{3}{8} (t^2 + 2u) + I_{(1, 2]} (t) \dfrac{9}{14} t^2 u^2\), \(0 \le u \le 1\)
\(f_X (t) = I_{[0, 1]} (t) \dfrac{3}{8} \int_{0}^{1} (t^2 + 2u) du + I_{(1, 2]} (t) \dfrac{9}{14} \int_{0}^{1} t^2 u^2 du = I_{[0,1]} (t) \dfrac{3}{8} (t^2 + 1) + I_{(1, 2]} (t) \dfrac{3}{14} t^2\)
\(f_Y(u) = \dfrac{3}{8} \int_{0}^{1} (t^2 + 2u0 dt + \dfrac{9}{14} \int_{1}^{2} t^2 u^2 dt = \dfrac{1}{8} + \dfrac{3}{4} u + \dfrac{3}{2} u^2\) \(0 \le u \le 1\)
\(P1 = \dfrac{3}{8} \int_{1/2}^{1} \int_{0}^{1/2} (t^2 + 2u) dudt + \dfrac{9}{14} \int_{1}^{3/2} \int_{0}^{1/2} t^2 u^2 dudt = 55/448\)
tuappr Enter matrix [a b] of X-range endpoints [0 2] Enter matrix [c d] of Y-range endpoints [0 1] Enter number of X approximation points 400 Enter number of Y approximation points 200 Enter expression for joint density (3/8)*(t.^2+2*u).*(t<=1) ... + (9/14)*(t.^2.*u.^2).*(t > 1) Use array operations on X, Y, PX, PY, t, u, and P M = (1/2<=t)&(t<=3/2)&(u<=1/2); P = total(M.*P) P = 0.1228 % Theoretical = 55/448 = 0.1228