The Midpoint
- Page ID
- 4737
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Outcomes
- Find the midpoint between two numbers.
- Sketch the midpoint of two numbers on a number line.
As the word sounds, "midpoint" means "the point in the middle". Finding a midpoint is not too difficult and has applications in many areas of statistics, from confidence intervals to sketching distributions, to means.
Finding the Midpoint Between Two Numbers
If we are given two numbers, then the midpoint is just the average of the two numbers. To calculate the midpoint, we add them up and then divide the result by 2. The formula is as follows:
Definition: the Midpoint
Let \(a\) and \(b\) be two numbers. Then the midpoint, \(M\) of these two numbers is
\[M\:=\frac{a+b}{2} \label{midpoint}\]
Example \(\PageIndex{1}\)
Find the midpoint of the numbers \(3.5\) and \(7.2\).
Solution
The most important thing about finding the midpoint is that the addition of the two numbers must occur before the division by 2. We can either do this one step at a time in our calculator or we can enclose the sum in parentheses. In this example we will perform the addition first:
\[3.5+7.2\:=\:10.7 \nonumber\]
Now we are ready to divide by 2:
\[\frac{10.7}{2}=5.35 \nonumber\]
Thus the midpoint of 3.5 and 7.2 is 5.35.
Example \(\PageIndex{2}\)
A major topic in statistics is the confidence interval which tells us the most likely interval that the mean or the proportion will lie in. Often the lower and upper bound of the confidence interval are given, but the midpoint of these two numbers is the best guess for what we are looking for. Suppose a 95% confidence interval for the difference between two means is -1.34 and 2.79. Find the midpoint of these numbers, which is the best guess for the difference between the two means.
Solution
We use the formula for the midpoint (Equation \ref{midpoint}):
\[M\:=\:\frac{a+b}{2}=\:\frac{-1.34+2.79}{2} \nonumber\]
Now let's use a calculator. We will need parentheses around the numerator:
\[\left(-1.34+2.79\right)\div2\:=\:0.725 \nonumber\]
Thus, the midpoint of the numbers -1.34 and 2.79 is 0.725.
Sketching the Midpoint on a Number Line
Visualizing the midpoint can often reveal it much better than just writing down its value. The diagrams are of fundamental importance in statistics.
Example \(\PageIndex{3}\)
Sketch the points -3, 5 and the midpoint of these two numbers on a number line.
Solution
We start by finding the midpoint using the midpoint formula (Equation \ref{midpoint}):
\[M\:=\frac{\:-3+5}{2}=\left(-3+5\right)\div2\:=\:1 \nonumber\]
Now we sketch these three points on the number line:

Example \(\PageIndex{4}\): hypothesis testing
Another application of the midpoint involves hypothesis testing. Sometimes we are given the hypothesized mean, which is the midpoint. We are also given the sample mean, which is either the left or right endpoint. The goal is to find the other endpoint. Suppose that the midpoint (hypothesized mean) is at 3.8 and the right endpoint (sample mean) is at 5.1. Find the value of the left endpoint.
Solution
It helps to sketch the diagram on the number line as shown below.
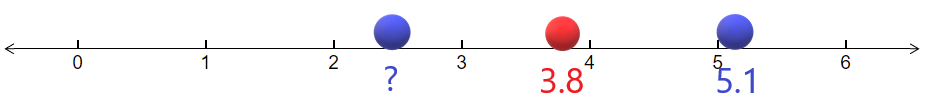
Now since 3.8 is the midpoint, the distance from the left endpoint to the midpoint is equal to the distance from 3.8 to 5.1. The distance from 3.8 to 5.1 is:
\[5.1\:-\:3.8\:=\:1.3 \nonumber\]
Therefore the left endpoint is 1.3 to the left of 3.8. This can be found by subtracting the two numbers:
\[3.8\:-\:1.3\:=\:2.5 \nonumber\]
Therefore the left endpoint is at 2.5.
Exercise
Suppose that the midpoint (hypothesized proportion) is at 0.31 and the left endpoint (sample proportion) is at 0.28. Find the value of the right endpoint.


