2.1: Qualitative Data
- Page ID
- 5164
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Remember, qualitative data are words describing a characteristic of the individual. There are several different graphs that are used for qualitative data. These graphs include bar graphs, Pareto charts, and pie charts.
Pie charts and bar graphs are the most common ways of displaying qualitative data. A spreadsheet program like Excel can make both of them. The first step for either graph is to make a frequency or relative frequency table. A frequency table is a summary of the data with counts of how often a data value (or category) occurs.
Example \(\PageIndex{1}\)
Suppose you have the following data for which type of car students at a college drive?
Ford, Chevy, Honda, Toyota, Toyota, Nissan, Kia, Nissan, Chevy, Toyota, Honda, Chevy, Toyota, Nissan, Ford, Toyota, Nissan, Mercedes, Chevy, Ford, Nissan, Toyota, Nissan, Ford, Chevy, Toyota, Nissan, Honda, Porsche, Hyundai, Chevy, Chevy, Honda, Toyota, Chevy, Ford, Nissan, Toyota, Chevy, Honda, Chevy, Saturn, Toyota, Chevy, Chevy, Nissan, Honda, Toyota, Toyota, Nissan
Solution
A listing of data is too hard to look at and analyze, so you need to summarize it. First you need to decide the categories. In this case it is relatively easy; just use the car type. However, there are several cars that only have one car in the list. In that case it is easier to make a category called other for the ones with low values. Now just count how many of each type of cars there are. For example, there are 5 Fords, 12 Chevys, and 6 Hondas. This can be put in a frequency distribution:
| Cateogry | Frequency |
|---|---|
| Ford | 5 |
| Chevy | 12 |
| Honda | 6 |
| Toyota | 12 |
| Nissan | 10 |
| Other | 5 |
| Total | 50 |
The total of the frequency column should be the number of observations in the data.
Since raw numbers are not as useful to tell other people it is better to create a third column that gives the relative frequency of each category. This is just the frequency divided by the total. As an example for Ford category:
relative frequency \(= \dfrac{5}{50} = 0.10\)
This can be written as a decimal, fraction, or percent. You now have a relative frequency distribution:
| Category | Frequency | Relative Frequency |
|---|---|---|
| Ford | 5 | 0.10 |
| Chevy | 12 | 0.24 |
| Honda | 6 | 0.12 |
| Toyota | 12 | 0.24 |
| Nissan | 10 | 0.20 |
| Other | 5 | 0.10 |
| Total | 50 | 1.00 |
The relative frequency column should add up to 1.00. It might be off a little due to rounding errors.
Now that you have the frequency and relative frequency table, it would be good to display this data using a graph. There are several different types of graphs that can be used: bar chart, pie chart, and Pareto charts.
Bar graphs or charts consist of the frequencies on one axis and the categories on the other axis. Then you draw rectangles for each category with a height (if frequency is on the vertical axis) or length (if frequency is on the horizontal axis) that is equal to the frequency. All of the rectangles should be the same width, and there should be equally width gaps between each bar.
Example \(\PageIndex{2}\) drawing a bar graph
Draw a bar graph of the data in Example \(\PageIndex{1}\).
Solution
| Category | Frequency | Relative Frequency |
|---|---|---|
| Ford | 5 | 0.10 |
| Chevy | 12 | 0.24 |
| Honda | 6 | 0.12 |
| Toyota | 12 | 0.24 |
| Nissan | 10 | 0.20 |
| Other | 5 | 0.10 |
| Total | 50 | 1.00 |
Put the frequency on the vertical axis and the category on the horizontal axis.
Then just draw a box above each category whose height is the frequency.
All graphs are drawn using \(R\). The command in \(R\) to create a bar graph is:
variable<-c(type in percentages or frequencies for each class with commas in between values)
barplot(variable,names.arg=c("type in name of 1st category", "type in name of 2nd category",…,"type in name of last category"),
ylim=c(0,number over max), xlab="type in label for x-axis", ylab="type in label for y-axis",ylim=c(0,number above maximum y value), main="type in title", col="type in a color") – creates a bar graph of the data in a color if you want.
For this example the command would be:
car<-c(5, 12, 6, 12, 10, 5)
barplot(car, names.arg=c("Ford", "Chevy", "Honda", "Toyota", "Nissan", "Other"), xlab="Type of Car", ylab="Frequency", ylim=c(0,12), main="Type of Car Driven by College Students", col="blue")
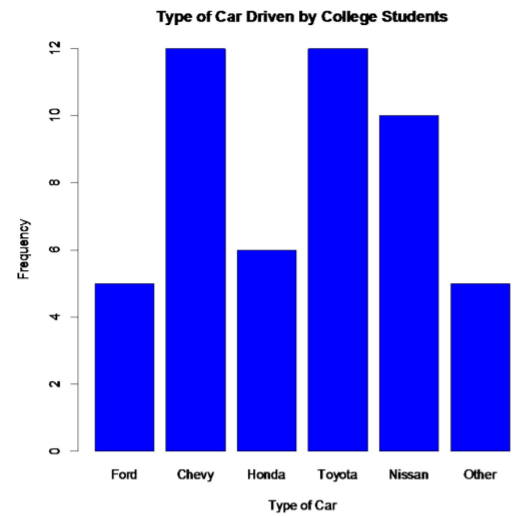.png?revision=1)
Notice from the graph, you can see that Toyota and Chevy are the more popular car, with Nissan not far behind. Ford seems to be the type of car that you can tell was the least liked, though the cars in the other category would be liked less than a Ford.
Some key features of a bar graph:
- Equal spacing on each axis.
- Bars are the same width.
- There should be labels on each axis and a title for the graph.
- There should be a scaling on the frequency axis and the categories should be listed on the category axis.
- The bars don’t touch.
You can also draw a bar graph using relative frequency on the vertical axis. This is useful when you want to compare two samples with different sample sizes. The relative frequency graph and the frequency graph should look the same, except for the scaling on the frequency axis.
Using R, the command would be:
car<-c(0.1, 0.24, 0.12, 0.24, 0.2, 0.1)
barplot(car, names.arg=c("Ford", "Chevy", "Honda", "Toyota", "Nissan", "Other"), xlab="Type of Car", ylab="Relative Frequency", main="Type of Car Driven by College Students", col="blue", ylim=c(0,.25))
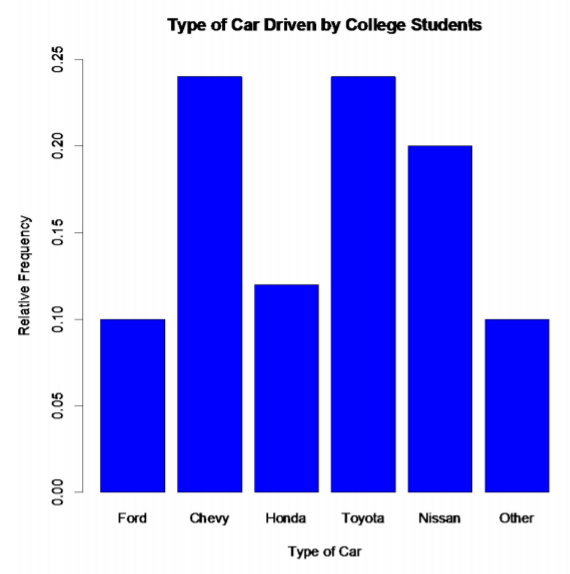.png?revision=1)
Another type of graph for qualitative data is a pie chart. A pie chart is where you have a circle and you divide pieces of the circle into pie shapes that are proportional to the size of the relative frequency. There are 360 degrees in a full circle. Relative frequency is just the percentage as a decimal. All you have to do to find the angle by multiplying the relative frequency by 360 degrees. Remember that 180 degrees is half a circle and 90 degrees is a quarter of a circle
Example \(\PageIndex{3}\) drawing a pie chart
Draw a pie chart of the data in Example \(\PageIndex{1}\).
First you need the relative frequencies.
| Category | Frequency | Relative Frequency |
|---|---|---|
| Ford | 5 | 0.10 |
| Chevy | 12 | 0.24 |
| Honda | 6 | 0.12 |
| Toyota | 12 | 0.24 |
| Nissan | 10 | 0.20 |
| Other | 5 | 0.10 |
| Total | 50 | 1.00 |
Solution
Then you multiply each relative frequency by 360° to obtain the angle measure for each category.
| Category | Relative Frequency | Angle (in degrees (°)) |
|---|---|---|
| Ford | 0.10 | 36.0 |
| Chevy | 0.24 | 86.4 |
| Honda | 0.12 | 43.2 |
| Toyota | 0.24 | 86.4 |
| Nissan | 0.20 | 72.0 |
| Other | 0.10 | 36.0 |
| Total | 1.00 | 360.0 |
Now draw the pie chart using a compass, protractor, and straight edge. Technology is preferred. If you use technology, there is no need for the relative frequencies or the angles.
You can use R to graph the pie chart. In R, the commands would be:
pie(variable,labels=c("type in name of 1st category", "type in name of 2nd category",…,"type in name of last category"),main="type in title", col=rainbow(number of categories)) – creates a pie chart with a title and rainbow of colors for each category.
For this example, the commands would be:
car<-c(5, 12, 6, 12, 10, 5)
pie(car, labels=c("Ford, 10%", "Chevy, 24%", "Honda, 12%", "Toyota, 24%", "Nissan, 20%", "Other, 10%"), main="Type of Car Driven by College Students", col=rainbow(6))
.png?revision=1)
As you can see from the graph, Toyota and Chevy are more popular, while the cars in the other category are liked the least. Of the cars that you can determine from the graph, Ford is liked less than the others.
Pie charts are useful for comparing sizes of categories. Bar charts show similar information. It really doesn’t matter which one you use. It really is a personal preference and also what information you are trying to address. However, pie charts are best when you only have a few categories and the data can be expressed as a percentage. The data doesn’t have to be percentages to draw the pie chart, but if a data value can fit into multiple categories, you cannot use a pie chart. As an example, if you are asking people about what their favorite national park is, and you say to pick the top three choices, then the total number of answers can add up to more than 100% of the people involved. So you cannot use a pie chart to display the favorite national park.
A third type of qualitative data graph is a Pareto chart, which is just a bar chart with the bars sorted with the highest frequencies on the left. Here is the Pareto chart for the data in Example \(\PageIndex{1}\).
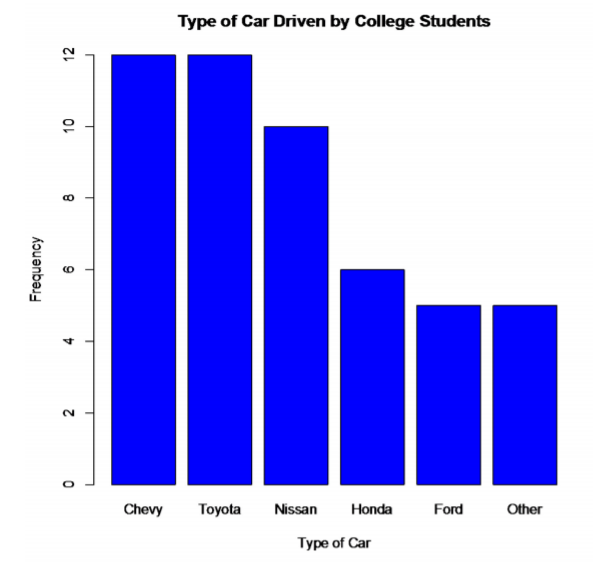.png?revision=1)
The advantage of Pareto charts is that you can visually see the more popular answer to the least popular. This is especially useful in business applications, where you want to know what services your customers like the most, what processes result in more injuries, which issues employees find more important, and other type of questions like these.
There are many other types of graphs that can be used on qualitative data. There are spreadsheet software packages that will create most of them, and it is better to look at them to see what can be done. It depends on your data as to which may be useful. The next example illustrates one of these types known as a multiple bar graph.
Example \(\PageIndex{4}\) multiple bar graph
In the Wii Fit game, you can do four different types of exercises: yoga, strength, aerobic, and balance. The Wii system keeps track of how many minutes you spend on each of the exercises everyday. The following graph is the data for Dylan over one week time period. Discuss any indication you can infer from the graph.
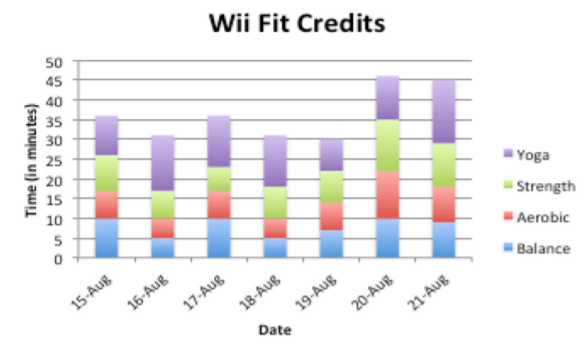.png?revision=1)
Solution
It appears that Dylan spends more time on balance exercises than on any other exercises on any given day. He seems to spend less time on strength exercises on a given day. There are several days when the amount of exercise in the different categories is almost equal.
The usefulness of a multiple bar graph is the ability to compare several different categories over another variable, in Example \(\PageIndex{4}\) the variable would be time. This allows a person to interpret the data with a little more ease.
Homework
Exercise \(\PageIndex{1}\)
- Eyeglassomatic manufactures eyeglasses for different retailers. The number of lenses for different activities is in Example \(\PageIndex{4}\).
Activity Grind Multicoat Assemble Make frames Receive finished Unknown Number of lenses 18872 12105 4333 25880 26991 1508 Table \(\PageIndex{4}\): Data for Eyeglassomatic
Grind means that they ground the lenses and put them in frames, multicoat means that they put tinting or scratch resistance coatings on lenses and then put them in frames, assemble means that they receive frames and lenses from other sources and put them together, make frames means that they make the frames and put lenses in from other sources, receive finished means that they received glasses from other source, and unknown means they do not know where the lenses came from. Make a bar chart and a pie chart of this data. State any findings you can see from the graphs. - To analyze how Arizona workers ages 16 or older travel to work the percentage of workers using carpool, private vehicle (alone), and public transportation was collected. Create a bar chart and pie chart of the data in Example \(\PageIndex{5}\). State any findings you can see from the graphs.
Transportation type Percentage Carpool 11.6% Private Vehicle (Alone) 75.8% Public Transportation 2.0% Other 10.6% Table \(\PageIndex{5}\): Data of Travel Mode for Arizona Workers - The number of deaths in the US due to carbon monoxide (CO) poisoning from generators from the years 1999 to 2011 are in table #2.1.6 (Hinatov, 2012). Create a bar chart and pie chart of this data. State any findings you see from the graphs.
Region Number of Deaths from CO While Using a Generator Urban Core 401 Sub-Urban 97 Large Rural 86 Small Rural/Isolated 111 Table \(\PageIndex{6}\): Data of Number of Deaths Due to CO Poisoning - In Connecticut households use gas, fuel oil, or electricity as a heating source. Example \(\PageIndex{7}\) shows the percentage of households that use one of these as their principle heating sources ("Electricity usage," 2013), ("Fuel oil usage," 2013), ("Gas usage," 2013). Create a bar chart and pie chart of this data. State any findings you see from the graphs.
Heating Source Percentage Electricity 15.3% Fuel Oil 46.3% Gas 35.6% Other 2.85 Table \(\PageIndex{7}\): Data of Household Heating Sources - Eyeglassomatic manufactures eyeglasses for different retailers. They test to see how many defective lenses they made during the time period of January 1 to March 31. Example \(\PageIndex{8}\) gives the defect and the number of defects. Create a Pareto chart of the data and then describe what this tells you about what causes the most defects.
Defect type Number of defects Scratch 5865 Right shaped - small 4613 Flaked 1992 Wrong axis 1838 Chamfer wrong 1596 Crazing, cracks 1546 Wrong shape 1485 Wrong PD 1398 Spots and bubbles 1371 Wrong height 1130 Right shape - big 1105 Lost in lab 976 Spots/bubble - intern 976 Table \(\PageIndex{8}\): Data of Defect Type - People in Bangladesh were asked to state what type of birth control method they use. The percentages are given in Example \(\PageIndex{9}\) ("Contraceptive use," 2013). Create a Pareto chart of the data and then state any findings you can from the graph.
Method Percentage Condom 4.50% Pill 28.50% Periodic Abstinence 4.90% Injection 7.00% Female Sterilization 5.00% IUD 0.90% Male Sterilization 0.70% Withdrawal 2.90% Other Modern Methods 0.70% Other Traditional Methods 0.60% Table \(\PageIndex{9}\): Data of Birth Control Type - The percentages of people who use certain contraceptives in Central American countries are displayed in Graph 2.1.6 ("Contraceptive use," 2013). State any findings you can from the graph.
.png?revision=1)
- Answer
-
See solutions


