18.2: Effect Sizes
- Page ID
- 8810
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)“Statistical significance is the least interesting thing about the results. You should describe the results in terms of measures of magnitude – not just, does a treatment affect people, but how much does it affect them.” Gene Glass (REF)
In the last chapter, we discussed the idea that statistical significance may not necessarily reflect practical significance. In order to discuss practical significance, we need a standard way to describe the size of an effect in terms of the actual data, which we refer to as an effect size. In this section we will introduce the concept and discuss various ways that effect sizes can be calculated.
An effect size is a standardized measurement that compares the size of some statistical effect to a reference quantity, such as the variability of the statistic. In some fields of science and engineering, this idea is referred to as a “signal to noise ratio”. There are many different ways that the effect size can be quantified, which depend on the nature of the data.
18.2.1 Cohen’s D
One of the most common measures of effect size is known as Cohen’s d, named after the statistician Jacob Cohen (who is most famous for his 1994 paper titled “The Earth Is Round (p < .05)”). It is used to quantify the difference between two means, in terms of their standard deviation:
where and are the means of the two groups, and is the pooled standard deviation (which is a combination of the standard deviations for the two samples, weighted by their sample sizes):
where and are the sample sizes and and are the standard deviations for the two groups respectively. Note that this is very similar in spirit to the t statistic — the main difference is that the denominator in the t statistic is based on the standard error of the mean, whereas the denominator in Cohen’s D is based on the standard deviation of the data. This means that while the t statistic will grow as the sample size gets larger, the value of Cohen’s D will remain the same.
There is a commonly used scale for interpreting the size of an effect in terms of Cohen’s d:
| D | Interpretation |
|---|---|
| 0.0 - 0.2 | neglibible |
| 0.2 - 0.5 | small |
| 0.5 - 0.8 | medium |
| 0.8 - | large |
It can be useful to look at some commonly understood effects to help understand these interpretations. For example, the effect size for gender differences in height (d = 1.6) is very large by reference to our table above. We can also see this by looking at the distributions of male and female heights in our sample. Figure 18.2 shows that the two distributions are quite well separated, though still overlapping, highlighting the fact that even when there is a very large effect size for the difference between two groups, there will be individuals from each group that are more like the other group.
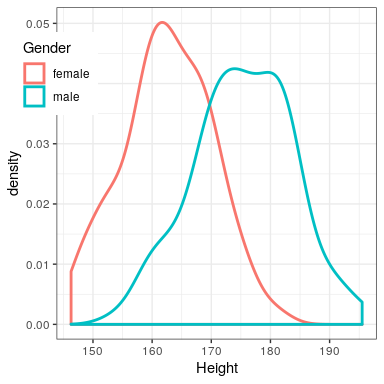
It is also worth noting that we rarely encounter effects of this magnitude in science, in part because they are such obvious effects that we don’t need scientific research to find them. As we will see in Chapter 32 on reproducibility, very large reported effects in scientific research often reflect the use of questionable research practices rather than truly huge effects in nature. It is also worth noting that even for such a huge effect, the two distributions still overlap - there will be some females who are taller than the average male, and vice versa. For most interesting scientific effects, the degree of overlap will be much greater, so we shouldn’t immediately jump to strong conclusions about different populations based on even a large effect size.
18.2.2 Pearson’s r
Pearson’s r, also known as the correlation coefficient, is a measure of the strength of the linear relationship between two continuous variables. We will discuss correlation in much more detail in Chapter 24, so we will save the details for that chapter; here, we simply introduce r as a way to quantify the relation between two variables.
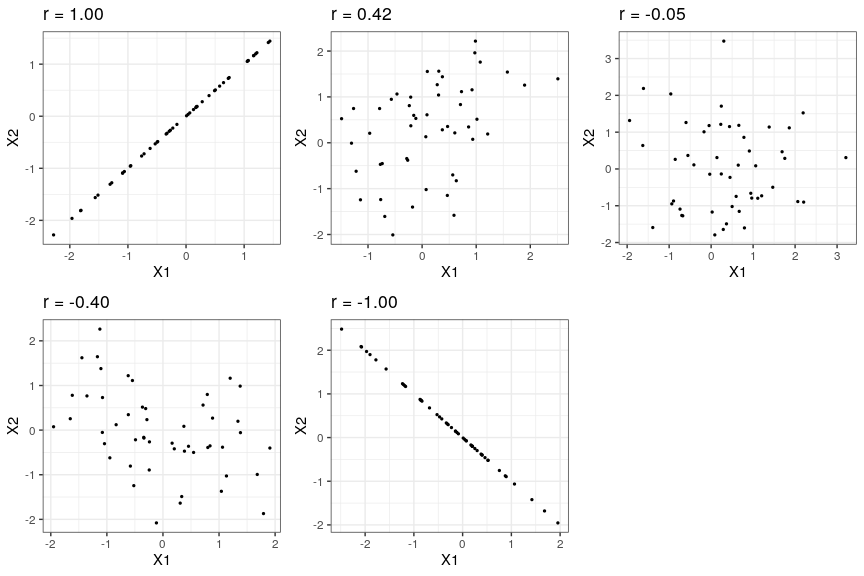
r is a measure that varies from -1 to 1, where a value of 1 represents a perfect positive relationship between the variables, 0 represents no relationship, and -1 represents a perfect negative relationship. Figure 18.3 shows examples of various levels of correlation using randomly generated data.
18.2.3 Odds ratio
In our earlier discussion of probability we discussed the concept of odds – that is, the relative likelihood of some event happening versus not happening:
We also discussed the odds ratio, which is simply the ratio of two odds. The odds ratio is a useful way to describe effect sizes for binary variables.
For example, let’s take the case of smoking and lung cancer. A study published in the International Journal of Cancer in 2012 (Pesch et al. 2012) combined data regarding the occurrence of lung cancer in smokers and individuals who have never smoked across a number of different studies. Note that these data come from case-control studies, which means that participants in the studies were recruited because they either did or did not have cancer; their smoking status was then examined. These numbers thus do not represent the prevalence of cancer amongst smokers in the general population – but they can tell us about the relationship between cancer and smoking.
| Status | NeverSmoked | CurrentSmoker |
|---|---|---|
| No Cancer | 2883 | 3829 |
| Cancer | 220 | 6784 |
We can convert these numbers to odds ratios for each of the groups. The odds of someone having lung cancer who has never smoked is 0.08 whereas the odds of a current smoker having lung cancer is 1.77. The ratio of these odds tells us about the relative likelihood of cancer between the two groups: The odds ratio of 23.22 tells us that the odds of cancer in smokers are roughly 23 times higher than never-smokers.


