8.1: Introduction

Last updated
Save as PDF

Page ID: 24055

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A statistic is a characteristic or measure from a sample. A parameter is a characteristic or measure from a population. We use statistics to generalize about parameters, known as estimations. Every time we take a sample statistic, we would expect that estimate to be close to the parameter, but not necessarily exactly equal to the unknown population parameter. How close would depend on how large a sample we took, who was sampled, how they were sampled and other factors. Hypothesis testing is a scientific method used to evaluate claims about population parameters.

A statistical hypothesis is an educated conjecture about a population parameter. This conjecture may or may not be true. We will take sample data and infer from the sample if there is evidence to support our claim about the unknown population parameter.

The null hypothesis (H₀, pronounced “H-naught” or “H-zero”), is a statistical hypothesis that states that there is no difference between a parameter and a specific value, or that there is no difference between two parameters. The null hypothesis is assumed true until there is sufficient evidence otherwise.

The alternative hypothesis (H₁ or H_a, pronounced “H-one” or “H-ā”), is a statistical hypothesis that states that there is a difference between a parameter and a specific value, or that there is a difference between two parameters. H₁ is always the complement of H₀.

The researcher decides the probability that the test is true by setting the level of significance, also called the significance level. We use the Greek letter α, pronounced “alpha,” to represent the significance level. The level of significance is the probability that the null hypothesis is rejected when it is actually true. Note: like in the previous chapter, 1 – $\alpha$ is the confidence level.

When doing your own research, you should set up their hypotheses and choose the significance level before analyzing the sample data.

When reading a word problem, your first step is to identify the parameter(s), for example μ, you are testing and which direction (left, right, or two-tail) test you are being asked to perform. For this course, the homework problems will state the researcher’s claim; usually this is the alternative hypothesis.

The null-hypothesis is always set up as a parameter equal to some value (called the test value) or equal to another parameter. The null hypothesis is assumed true unless there is strong evidence from the sample to suggest otherwise. Similar to our judicial system that a person is innocent until the prosecutor shows enough evidence that they are not innocent.

For example, an investment company wants to build a new food cart. They know from experience that food carts are successful if they have on average more than 100 people a day walk by the location. They have a potential site to build on, but before they begin, they want to see if they have enough foot traffic. They observe how many people walk by the site every day over a month. The investors want to be very careful about setting up in a bad location where the food cart will fail, rather than the missed opportunity build in a prime location. We have two hypotheses. For an average of more than 100 people, we would write this in symbols as μ > 100. This claim needs to go into the alternative hypothesis since there is no equality, just strictly greater than 100. The complement of greater than is μ ≤ 100. This has a form of equality (≤) so needs to go in the null hypothesis.

We then would set up the hypotheses as:

H₀: μ ≤ 100 (Do not build)
H₁: μ > 100 (Build).

When performing the hypothesis test, the test statistic assumes that the parameter is the null hypothesis equal to some value. This still implies that the parameter could be any value less than or equal to 100 but our hypothesis test should be written as:

H₀: μ = 100
H₁: μ > 100

Either notation is fine, but most textbooks will always have the = sign in the null hypothesis. The null hypothesis is based off historical value, a claim or product specification.

Signs are Important

When there is a greater than sign (>) in the alternative hypothesis, we call this a right-tailed test. If we had a less than sign (<) in the alternative hypothesis, then we would have a left-tailed test. If there were a not equal sign (≠) in the alternative hypothesis, we would have a two-tailed test. The tails will determine which side the critical region will fall on the sampling distribution. Note that you should never have an =, ≤ or ≥ sign appear in the alternative hypothesis.

There are three ways to set up the hypotheses for a population mean μ:

Two-tailed test Right-tailed test Left-tailed test

$\begin{array}{lll}
\mathrm{H}_{0}: \mu=\mu_{0} & \mathrm{H}_{0}: \mu=\mu_{0} & \mathrm{H}_{0}: \mu=\mu_{0} \\
\mathrm{H}_{1}: \mu \neq \mu_{0} & \mathrm{H}_{1}: \mu>\mu_{0} & \mathrm{H}_{1}: \mu<\mu_{0}
\end{array}$

Two-tailed test Right-tailed test Left-tailed test

$\begin{array}{lll}
\mathrm{H}_{0}: \mu=\mu_{0} & \mathrm{H}_{0}: \mu \leq \mu_{0} & \mathrm{H}_{0}: \mu \geq \mu_{0} \\
\mathrm{H}_{1}: \mu \neq \mu_{0} & \mathrm{H}_{1}: \mu>\mu_{0} & \mathrm{H}_{1}: \mu<\mu_{0}
\end{array}$

where μ₀ is a placeholder for the numeric test value.

The null-hypothesis of a two-tailed test states that the mean μ is equal to some value μ₀.
The null-hypothesis of a right-tailed test implies that the mean μ is less than or equal to some value μ₀.
The null-hypothesis of a left-tailed test implies that the mean μ is greater than or equal to some value μ₀.

Look for key phrases in the research question to help you set up the hypotheses. Make sure that the =, ≤ and ≥ sign always go in the null hypothesis. The ≠, > and < sign always go in the alternative hypothesis. Look for these phrases in Figure 8-1 to help you decide if you are setting up a two-tailed test (first column), a right-tailed test (second column), or left-tailed test (third column).

When you read a question, it is essential that you identify the parameter of interest. The parameter determines which distribution to use. Make sure that you can recognize and distinguish which parameter you are making a conjecture about: mean = µ, proportion = p, variance = σ² , standard deviation = σ. There will be more parameters in later chapters.

Do not use the sample statistics, like $\overline{ x }$ or $\hat{p}$, in the hypotheses. We are not making any inference about the sample statistics. We know the value of the sample statistic. We use the sample statistics to infer if a change has occurred in the population.

For example, if we were making a conjecture about the percent or proportion in a population we would have the hypotheses:

H_0: p = p₀

H₁: p ≠ p₀.

Setting up the hypotheses correctly is the most important step in hypothesis testing. Here are some example research questions and how to set up the null and alternative hypotheses correctly; in a later section, we will perform the entire hypothesis test.

Use Figure 8-1 as a guide in setting up your hypotheses. The first column shows the hypotheses and how to shade in the distribution for a two-tailed test, with common phrases in the claim. The two-tailed test will always have a not equal ≠ sign in the alternative hypothesis and both tails shaded. The second column is for a right-tailed test. Note that the greater than > sign always will be in the alternative hypothesis and the right tail is shaded. The third column is for a left-tailed test. The left-tailed test will always have a less than < sign in the alternative hypothesis and the left tail shaded in.

Hypothesis Testing Common Phrases

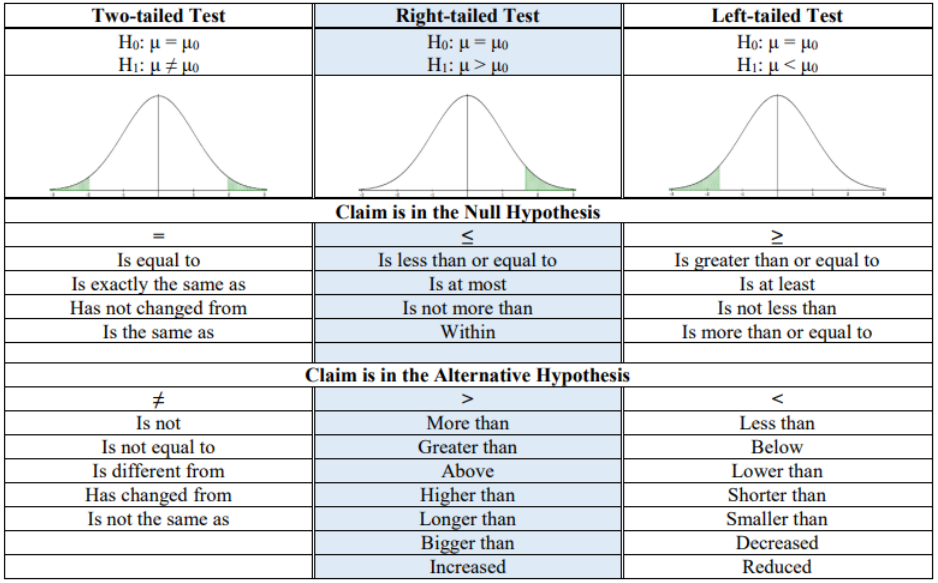
Figure 8-1

State the hypotheses in both words and symbols for the following claims.

The national mean salary for high school teachers is $61,420. A random sample of 30 teacher’s salaries had a mean of $49,850. A new director for a graduate teacher education program (GTEP) believes that the average salary of a teacher in Oregon is significantly less than national average.
A high school principal is looking into assigning parking spaces at their school if the proportion of students who own their own car is more than 30%. The principal does not have the time to ask all 1,200 students at their school so instead takes a random sample of 70 students and found that 33% owned their own car.
A teacher would like to know if the average age of students taking evening classes is different from the university’s average age of 26. They sample 40 students from a random sample of evening classes and found the average age to be 27.

Solution

a) The key phrase in the claim is “less than.” The less than sign < is only allowed in the alternative hypothesis and we are testing against the national average.

H₀: The national mean salary is $61,420.

H₁: The GTEP director believes the mean salary in Oregon is less than $61,420.

H₀: μ = 61420

H₁: μ < 61420

b) The key phrase in the claim is “more than.” The greater than sign > is only allowed in the alternative hypothesis. This is about a proportion, not a mean, so use the parameter p.

H₀: The principal will not assign parking spaces if 30% or less of students own a car.

H₁: The principal will assign parking spaces if more than 30% of students own a car.

H₀: p = 0.3

H₁: p > 0.3

c) The key word in the claim is “different.” The not equal sign ≠ is only allowed in the alternative hypothesis.

H₀: The population mean age is 26 years old.

H₁: The evening students’ mean age is believed to be different from 26 years old.

H₀: μ = 26

H₁: μ ≠ 26

Once we collect sample data we need to find out how far away the sample statistic can be from the hypothesized parameter to say that a statistically significant change has occurred.

Suppose a manufacturer of a new laptop battery claims the mean life of the battery is 900 days with a standard deviation of 40 days. You are the buyer of this battery and you think this claim is inflated. You would like to test your belief because without a good reason you cannot get out of your contract. You take a random sample of 35 batteries and find that the mean battery life is 890 days. What are the hypotheses for this question?

Solution

You have a guess that the mean life of a battery is less than 900 days. This is opposed to what the manufacturer claims. There really are two hypotheses, which are just guesses here – the one that the manufacturer claims and the one that you believe. For this problem:

H₀: μ = 900, since the manufacturer says the mean life of a battery is 900 days.

H₁: μ < 900, since you believe the mean life of the battery is less than 900 days.

Note that we do not put the sample mean of 890 in our hypotheses.

Is the sample mean of 890 days small enough to believe that you are right and the manufacturer is wrong? We would expect variation in our sample data and every time we take a new sample, the sample mean will most likely be different. How far away does the sample mean have to be from the product specification to verify our claim was correct? The sample data and the answer to these questions will be answered once we run the hypothesis test.

If you calculated a sample mean of 435, you would definitely believe the population mean is less than 900. However, even if you had a sample mean of 835 you would probably believe that the true mean was less than 900. What about 875? Or 893? There is some point where you would stop being so sure that the population mean is less than 900. That point separates the values of where you are sure or pretty sure that the mean is less than 900 from the area where you are not so sure.

How do you find that point where the sample mean is close enough to the hypothesized population mean? How close depends on how much error you want to make. Of course, you do not want to make any errors, but unfortunately, that is unavoidable in statistics since we are not measuring the entire population. You need to figure out how much error you made with your sample. Take the sample mean, and find the probability of getting another sample mean less than it, assuming for the moment that the manufacturer is right. The idea behind this is that you want to know what is the chance that you could have come up with your sample mean even if the population mean really is 900 days.

You want to find P($\bar{X}$ < 890 | H₀ is true) = P($\bar{X}$ < 890 | μ = 900). For short, we will call this probability the p-value or simply p.

To compute this p-value, you need to know how the sample mean is distributed. Since the sample size is at least 30 you know the sample mean is approximately normally distributed, by the Central Limit Theorem (CLT). Remember $\mu_{\bar{x}}=\mu$ and $\sigma_{\bar{x}}=\frac{\delta}{\sqrt{n}}$. Before calculating the probability, it is useful to see how many standard deviations away from the mean the sample mean is. Using the formula for the z-score for CLT, $z=\frac{\bar{x}-\mu}{\left(\frac{\sigma}{\sqrt{n}}\right)}$ we can compare this z-score to a zscore based on how sure we want to be of not making a mistake.

Using our sample mean we compute the z-score: $z=\frac{\bar{x}-\mu_{0}}{\left(\frac{\sigma}{\sqrt{n}}\right)}=\frac{890-900}{\left(\frac{40}{\sqrt{35}}\right)}=-1.479$. This sample mean is more than one standard deviation away from the mean. Is that far enough?

Look at the probability P($\bar{X}$ < 890 | H₀ is true) = P($\bar{X}$ < 890 | μ = 900) = P(Z < –1.479).

Using the TI Calculator normalcdf(-1E99,890,900,40/$\sqrt{35}$) $\approx$ 0.0696.

Alternatively, in Excel use =NORM.DIST(890,900,40/SQRT(35),TRUE) $\approx$ 0.0696.

Hence the p-value = 0.0696.

A picture is always useful. Figures 8-2 shows the populations distribution. Figure 8-3 shows the sampling distribution of the mean.

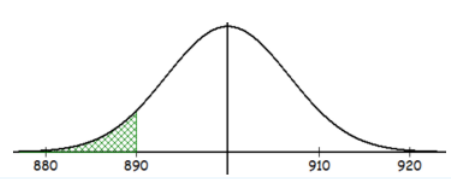
Figure 8-2

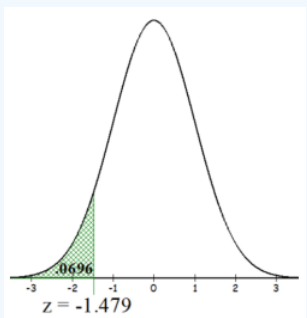
Figure 8-3

There is approximately a 6.96% chance that you could find a sample mean less than 890 when the population mean is 900 days. This is small but not really small. But how do you quantify really small? Is 5% or 10% or 15% really small? How do you decide? That depends on your field of study and the importance of the situation and will be answered in the next section.

To understand the process of a hypothesis test, you need to first understand what a hypothesis is, which is an educated guess about a parameter. Once you have the alternative hypothesis, you collect data and use the data to decide to see if there is enough evidence to show that the alternative hypothesis is true. However, in hypothesis testing you actually assume something else is true, the null hypothesis, and then you look at your data to see how likely it is to get an event that your data demonstrates with that assumption. If the event is very unusual, then you might think that your assumption is actually false. If you are able to say this assumption is false, then your alternative hypothesis could be true. You assume the opposite of your alternative hypothesis is true and show that it cannot be true. If this happens, then your alternative hypothesis is probably true. All hypothesis tests go through the same process. Once you have the process down, then the concept is much easier.

When setting up your hypotheses make sure the parameter, not the statistic, is used in the hypotheses. The equality always goes in the null hypothesis H₀ and the alternative hypothesis H_a will be a left-tailed test with a less than sign <, a two-tailed test with a not equal sign $\neq$, or a right-tailed test with a greater than sign >.

“‘But alright,’ went on the rumblings, ‘so what's the alternative?’

‘Well,’ said Ford, brightly but slowly, ‘stop doing it of course!’”

(Adams, 2002)