10.5: Statistical Inferences About β₁
- Page ID
- 546
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To learn how to construct a confidence interval for \(β_1\), the slope of the population regression line.
- To learn how to test hypotheses regarding \(β_1\).
The parameter \(β_1\), the slope of the population regression line, is of primary importance in regression analysis because it gives the true rate of change in the mean \( E(y)\) in response to a unit increase in the predictor variable \(x\). For every unit increase in \(x\) the mean of the response variable \(y\) changes by \(β_1\) units, increasing if \(β_1>0\) and decreasing if \(β_1 <0\). We wish to construct confidence intervals for \(β_1\) and test hypotheses about it.
Confidence Intervals for \(β_1\)
The slope \(\hat{β}_1\) of the least squares regression line is a point estimate of \(β_1\). A confidence interval for \(β_1\) is given by the following formula.
\[ \hat{β}_1 \pm t_{α/2} \dfrac{s_{\epsilon}}{\sqrt{SS_{xx}}} \nonumber \]
where \(S_\varepsilon =\sqrt{\frac{SSE}{n-2}}\) and the number of degrees of freedom is \(df=n-2\).
The assumptions listed in Section 10.3 must hold.
The statistic \(S_\varepsilon \) is called the sample standard deviation of errors. It estimates the standard deviation \(\sigma\) of the errors in the population of \(y\)-values for each fixed value of \(x\) (see Figure 10.3.1).
Construct the \(95\%\) confidence interval for the slope \(β_1\) of the population regression line based on the five-point sample data set
\[\begin{array}{c|c c c c c} x & 2 & 2 & 6 & 8 & 10 \\ \hline y &0 &1 &2 &3 &3\\ \end{array} \nonumber \]
Solution
The point estimate \(\hat{β}_1\) of \(β_1\) was computed in Example 10.4.2 as \(\hat{β}_1=0.34375\). In the same example \(SS_{xx}\) was found to be \(SS_{xx}=51.2\). The sum of the squared errors \(SSE\) was computed in Example 10.4.4 as \(SSE=0.75\). Thus
\[S_\varepsilon =\sqrt{\frac{SSE}{n-2}}=\sqrt{\frac{0.75}{3}}=0.50 \nonumber \]
Confidence level \(95\%\) means \(\alpha =1-0.95=0.05\) so \(\alpha /2=0.025\). From the row labeled \(df=3\) in Figure 7.1.6 we obtain \(t_{0.025}=3.182\). Therefore
\[\hat{\beta _1}\pm t_{\alpha /2}\frac{S_\varepsilon }{\sqrt{SS_{xx}}}=0.34375\pm 3.182\left ( \frac{0.50}{\sqrt{51.2}} \right )=0.34375\pm 0.2223 \nonumber \]
which gives the interval \((0.1215,0.5661)\). We are \(95\%\) confident that the slope \(β_1\) of the population regression line is between \(0.1215\) and \(0.5661\).
Using the sample data in Table 10.4.3 construct a \(90\%\) confidence interval for the slope \(β_1\) of the population regression line relating age and value of the automobiles of Example 10.4.3. Interpret the result in the context of the problem.
Solution
The point estimate \(\hat{β}_1\) of \(β_1\) was computed in Example 10.4.3, as was \(SS_{xx}\). Their values are \(\hat{β}_1=-2.05\) and \(SS_{xx}=14\). The sum of the squared errors \(SSE\) was computed in Example 10.4.5 as \(SSE=28.946\). Thus
\[S_\varepsilon =\sqrt{\frac{SSE}{n-2}}=\sqrt{\frac{28.946}{8}}=1.902169814 \nonumber \]
Confidence level \(90\%\) means \(\alpha =1-0.90=0.10\) so \(\alpha /2=0.05\). From the row labeled \(df=8\) in Figure 7.1.6 we obtain \(t_{0.05}=1.860\). Therefore
\[\hat{\beta _1}\pm t_{\alpha /2}\frac{S_\varepsilon }{\sqrt{SS_{xx}}}=-2.05\pm 1.860\left ( \frac{1.902169814}{\sqrt{14}} \right )=-2.05\pm 0.95 \nonumber \]
which gives the interval \((-3.00,-1.10)\). We are \(90\%\) confident that the slope \(β_1\) of the population regression line is between \(-3.00\) and \(-1.10\). In the context of the problem this means that for vehicles of this make and model between two and six years old we are \(90\%\) confident that for each additional year of age the average value of such a vehicle decreases by between \(\$1,100\) and \(\$3,000\).
Testing Hypotheses About β1
Hypotheses regarding \(β_1\) can be tested using the same five-step procedures, either the critical value approach or the \(p\)-value approach, that were introduced in Section 8.1 and Section 8.3. The null hypothesis always has the form \(H_0: \beta _1=B_0\) where \(B_0\) is a number determined from the statement of the problem. The three forms of the alternative hypothesis, with the terminology for each case, are:
| Form of \(H_a\) | Terminology |
|---|---|
| \(H_a: \beta _1<B_0\) | Left-tailed |
| \(H_a: \beta _1>B_0\) | Right-tailed |
| \(H_a: \beta _1\neq B_0\) | Two-tailed |
The value zero for \(B_0\) is of particular importance since in that case the null hypothesis is \(H_0: \beta _1=0\), which corresponds to the situation in which \(x\) is not useful for predicting \(y\). For if \(β_1=0\) then the population regression line is horizontal, so the mean \(E(y)\) is the same for every value of \(x\) and we are just as well off in ignoring \(x\) completely and approximating \(y\) by its average value. Given two variables \(x\) and \(y\), the burden of proof is that \(x\) is useful for predicting \(y\), not that it is not. Thus the phrase “test whether \(x\) is useful for prediction of \(y\),” or words to that effect, means to perform the test
\[H_0: \beta _1=0\; \; \text{vs.}\; \; H_a: \beta _1\neq 0 \nonumber \]
\[T=\frac{\hat{\beta _1}-B_0}{S_\varepsilon /\sqrt{SS_{xx}}} \nonumber \]
The test statistic has Student’s \(t\)-distribution with \(df=n-2\) degrees of freedom.
The assumptions listed in Section 10.3 must hold.
Test, at the \(2\%\) level of significance, whether the variable \(x\) is useful for predicting \(y\) based on the information in the five-point data set
\[\begin{array}{c|c c c c c} x & 2 & 2 & 6 & 8 & 10 \\ \hline y &0 &1 &2 &3 &3\\ \end{array} \nonumber \]
Solution
We will perform the test using the critical value approach.
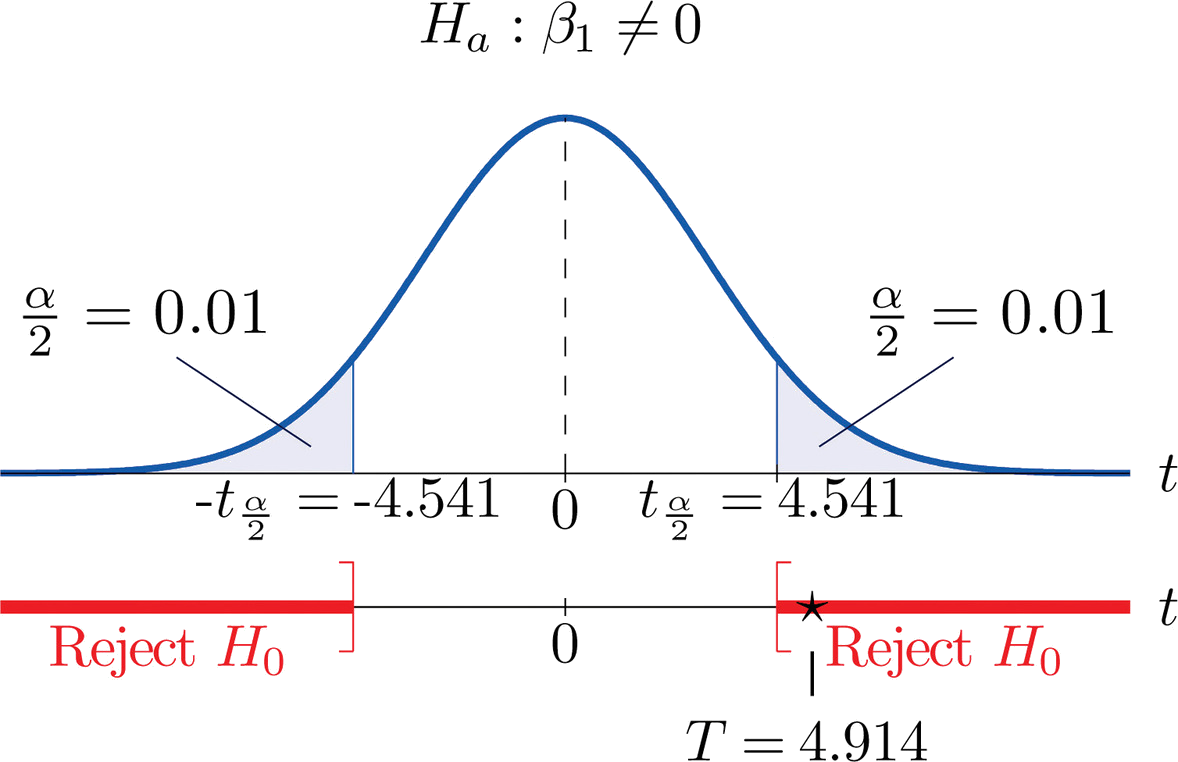
- Step 1. Since \(x\) is useful for prediction of \(y\) precisely when the slope \(β_1\) of the population regression line is nonzero, the relevant test is \[H_0: \beta _1=0\\ \text{vs.}\\ H_a: \beta _1\neq 0\; \; @\; \; \alpha =0.02 \nonumber \]
- Step 2. The test statistic is \[T=\frac{\hat{\beta _1}}{S_\varepsilon /\sqrt{SS_{xx}}} \nonumber \] and has Student’s \(t\)-distribution with \(n-2=5-2=3\) degrees of freedom.
- Step 3. From Example 10.4.1, \(β_1=0.34375 \) and \(SS_{xx}=51.2\). From "Example \(\PageIndex{1}\)", \(S_\varepsilon =0.50\). The value of the test statistic is therefore \[T=\frac{\hat{\beta _1}-B_0}{S_\varepsilon /\sqrt{SS_{xx}}}=\frac{0.34375}{0.50/\sqrt{51.2}}=4.919 \nonumber \]
- Step 4. Since the symbol in \(H_a\) is “\(\neq\)” this is a two-tailed test, so there are two critical values \(\pm t_{\alpha /2}=\pm t_{0.01}\). Reading from the line in Figure 7.1.6 labeled \(df=3\), \(t_{0.01}=4.541\). The rejection region is \[(-\infty ,-4.541]\cup [4.541,\infty ) \nonumber \].
- Step 5. As shown in Figure \(\PageIndex{1}\) "Rejection Region and Test Statistic for" the test statistic falls in the rejection region. The decision is to reject \(H_0\). In the context of the problem our conclusion is:
The data provide sufficient evidence, at the \(2\%\) level of significance, to conclude that the slope of the population regression line is nonzero, so that \(x\) is useful as a predictor of \(y\).
A car salesman claims that automobiles between two and six years old of the make and model discussed in Example 10.4.2 lose more than \(\$1,100\) in value each year. Test this claim at the \(5\%\) level of significance.
Solution
We will perform the test using the critical value approach.
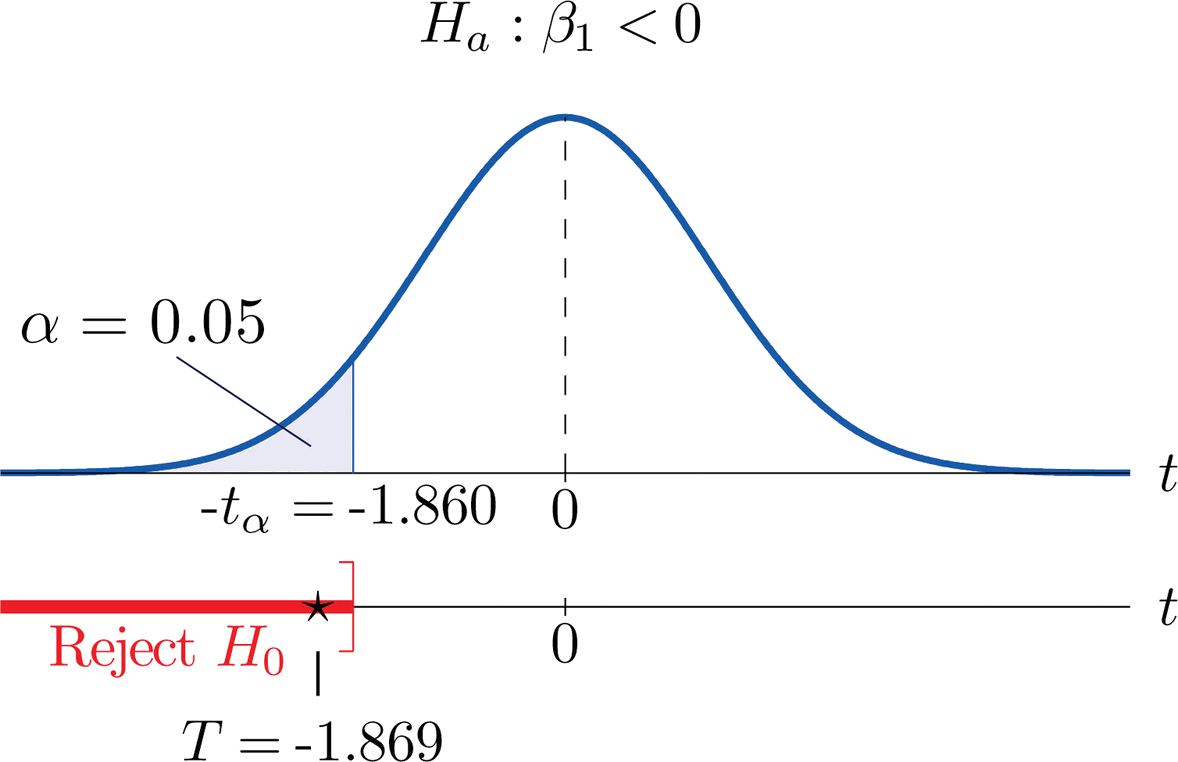
- Step 1. In terms of the variables \(x\) and \(y\), the salesman’s claim is that if \(x\) is increased by \(1\) unit (one additional year in age), then \(y\) decreases by more than \(1.1\) units (more than \(\$1,100\)). Thus his assertion is that the slope of the population regression line is negative, and that it is more negative than \(-1.1\). In symbols, \(β_1<-1.1\). Since it contains an inequality, this has to be the alternative hypotheses. The null hypothesis has to be an equality and have the same number on the right hand side, so the relevant test is \[H_0: \beta _1=-1.1\\ \text{vs.}\\ H_a: \beta _1<-1.1\; \; @\; \; \alpha =0.05 \nonumber \]
- Step 2. The test statistic is \[T=\frac{\hat{\beta _1}-B_0}{S_\varepsilon /\sqrt{SS_{xx}}} \nonumber \] and has Student’s \(t\)-distribution with \(8\) degrees of freedom.
- Step 3. From Example 10.4.2, \(β_1=-2.05\) and \(SS_{xx}=14\). From "Example \(\PageIndex{2}\)", \(S_\varepsilon =1.902169814\). The value of the test statistic is therefore \[T=\frac{\hat{\beta _1}-B_0}{S_\varepsilon /\sqrt{SS_{xx}}}=\frac{-2.05-(-1.1)}{1.902169814/\sqrt{14}}=-1.869 \nonumber \]
- Step 4. Since the symbol in \(H_a\) is “\(<\)” this is a left-tailed test, so there is a single critical value \(-t_{\alpha /2}=-t_{0.05}\). Reading from the line in Figure 7.1.6 labeled \(df=8\), \(t_{0.05}=1.860\). The rejection region is \[(-\infty ,-1.860] \nonumber \].
- Step 5. As shown in Figure \(\PageIndex{2}\) "Rejection Region and Test Statistic for " the test statistic falls in the rejection region. The decision is to reject \(H_0\). In the context of the problem our conclusion is:
The data provide sufficient evidence, at the \(5\%\) level of significance, to conclude that vehicles of this make and model and in this age range lose more than \(\$1,100\) per year in value, on average.
Key Takeaway
- The parameter \(β_1\), the slope of the population regression line, is of primary interest because it describes the average change in \(y\) with respect to unit increase in \(x\).
- The statistic \(\hat{β}_1\), the slope of the least squares regression line, is a point estimate of \(β_1\). Confidence intervals for \(β_1\) can be computed using a formula.
- Hypotheses regarding \(β_1\) are tested using the same five-step procedures introduced in Chapter 8.


