9.4: Comparison of Two Population Proportions
- Page ID
- 575
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To learn how to construct a confidence interval for the difference in the proportions of two distinct populations that have a particular characteristic of interest.
- To learn how to perform a test of hypotheses concerning the difference in the proportions of two distinct populations that have a particular characteristic of interest.
Suppose we wish to compare the proportions of two populations that have a specific characteristic, such as the proportion of men who are left-handed compared to the proportion of women who are left-handed. Figure \(\PageIndex{1}\) illustrates the conceptual framework of our investigation. Each population is divided into two groups, the group of elements that have the characteristic of interest (for example, being left-handed) and the group of elements that do not. We arbitrarily label one population as Population \(1\) and the other as Population \(2\), and subscript the proportion of each population that possesses the characteristic with the number \(1\) or \(2\) to tell them apart. We draw a random sample from Population \(1\) and label the sample statistic it yields with the subscript \(1\). Without reference to the first sample we draw a sample from Population \(2\) and label its sample statistic with the subscript \(2\).
Our goal is to use the information in the samples to estimate the difference \(p_1-p_2\) in the two population proportions and to make statistically valid inferences about it.
Confidence Intervals
Since the sample proportion \(\hat{p}_1\) computed using the sample drawn from Population \(1\) is a good estimator of population proportion \(p_1\) of Population \(1\) and the sample proportion \(\hat{p}_2\) computed using the sample drawn from Population \(2\) is a good estimator of population proportion \(p_2\) of Population \(2\), a reasonable point estimate of the difference \(p_1−p_2\) is \(\hat{p}_1 -\hat{p}_2\). In order to widen this point estimate into a confidence interval we suppose that both samples are large, as described in Section 7.3 and repeated below. If so, then the following formula for a confidence interval for \(p_1−p_2\) is valid.
\[(\hat{p}_1−\hat{p}_2) \pm z_{a/2} \sqrt{ \dfrac{ \hat{p}_1(1−\hat{p}_1)}{n_1}+ \dfrac{\hat{p}_2(1−\hat{p}_2)}{n_2}} \nonumber \]
The samples must be independent, and each sample must be large: each of the intervals
\[\left[ \hat{p}_1−3 \sqrt{ \dfrac{\hat{p}_1(1−\hat{p}_1)}{n_1}}, \hat{p}_1 + 3 \sqrt{ \dfrac{ \hat{p}_1(1−\hat{p}_1)}{n_1}} \right] \nonumber \]
and
\[\left[ \hat{p}_2−3 \sqrt{ \dfrac{\hat{p}_2(1−\hat{p}_2)}{n_2}}, \hat{p}_2 + 3 \sqrt{ \dfrac{ \hat{p}_2(1−\hat{p}_2)}{n_2}} \right] \nonumber \]
must lie wholly within the interval \([0,1]\).
The department of code enforcement of a county government issues permits to general contractors to work on residential projects. For each permit issued, the department inspects the result of the project and gives a “pass” or “fail” rating. A failed project must be re-inspected until it receives a pass rating. The department had been frustrated by the high cost of re-inspection and decided to publish the inspection records of all contractors on the web. It was hoped that public access to the records would lower the re-inspection rate. A year after the web access was made public, two samples of records were randomly selected. One sample was selected from the pool of records before the web publication and one after. The proportion of projects that passed on the first inspection was noted for each sample. The results are summarized below. Construct a point estimate and a \(90\%\) confidence interval for the difference in the passing rate on first inspection between the two time periods.
\[\begin{array}{c|c} \text{No public web access} & n_1=500\; \; \hat{p_1}=0.67 \\ \hline \text{Public web access} & n_2=100\; \; \hat{p_2}=0.80 \\ \end{array} \nonumber \]
Solution
The point estimate of \(p_1−p_2\) is
\[\hat{p}_1−\hat{p}_2=0.67−0.80=−0.13 \nonumber \]
Because the “No public web access” population was labeled as Population \(1\) and the “Public web access” population was labeled as Population \(2\), in words this means that we estimate that the proportion of projects that passed on the first inspection increased by \(13\) percentage points after records were posted on the web.
The sample sizes are sufficiently large for constructing a confidence interval since for sample 1:
\[ 3 \sqrt{ \dfrac{ \hat{p}_1(1−\hat{p}_1)}{n_1}} = 3 \sqrt{ \dfrac{ (0.67)(0.33)}{500}} =0.06 \nonumber \]
so that
\[\left [ \hat{p_1}-3\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}}, \hat{p_1}+3\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}} \right ]=[0.67-0.06,0.67+0.06]=[0.61,0.73]\subset [0,1] \nonumber \]
and for sample \(2\):
\[3\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}}=3\sqrt{\frac{(0.8)(0.2)}{100}}=0.12 \nonumber \]
so that
\[\left [ \hat{p_2}-3\sqrt{\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}, \hat{p_2}+3\sqrt{\frac{\hat{p_2}(1-\hat{p_2})}{n_2}} \right ]=[0.8-0.12,0.8+0.12]=[0.68,0.92]\subset [0,1] \nonumber \]
To apply the formula for the confidence interval, we first observe that the \(90\%\) confidence level means that \(\alpha =1-0.90=0.10\) so that \(z_{\alpha /2}=z_{0.05}\). From Figure 7.1.6 we read directly that \(z_{0.05}=1.645\). Thus the desired confidence interval is
\[\begin{align} (\hat{p}_1−\hat{p}_2)&± z_{α/2} \sqrt{ \dfrac{ \hat{p}_1(1−\hat{p}_1)}{n_1} + \dfrac{\hat{p}_2(1−\hat{p}_2)}{n_2}} \\ &= 0.13 ± 1.645 \sqrt{ \dfrac{(0.67)(0.33)}{500}+\dfrac{(0.8)(0.2)}{100}} \\ &= -0.13±0.07 \end{align} \nonumber \]
The \(90\%\) confidence interval is \([-0.20,-0.06]\). We are \(90\%\) confident that the difference in the population proportions lies in the interval \([-0.20,-0.06]\), in the sense that in repeated sampling \(90\%\) of all intervals constructed from the sample data in this manner will contain \(p_1−p_2\). Taking into account the labeling of the two populations, this means that we are \(90\%\) confident that the proportion of projects that pass on the first inspection is between \(6\) and \(20\) percentage points higher after public access to the records than before.
Hypothesis Testing
In hypothesis tests concerning the relative sizes of the proportions \(p_1\) and \(p_2\) of two populations that possess a particular characteristic, the null and alternative hypotheses will always be expressed in terms of the difference of the two population proportions. Hence the null hypothesis is always written
\[H_0: p_1−p_2=D_0 \nonumber \]
The three forms of the alternative hypothesis, with the terminology for each case, are:
| Form of \(H_a\) | Terminology |
|---|---|
| \(H_a : p _1−p_2 < D_0\) | Left-tailed |
| \(H_a : p_1−p_2>D_0\) | Right-tailed |
| \(H_a : p_1−p_2 \neq D_0\) | Two-tailed |
As long as the samples are independent and both are large the following formula for the standardized test statistic is valid, and it has the standard normal distribution.
\[Z=\frac{(\hat{p_1}-\hat{p_2})-D_0}{\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}} \nonumber \]
The test statistic has the standard normal distribution.
The samples must be independent, and each sample must be large: each of the intervals
\[\left [ \hat{p_1}-3\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}}, \hat{p_1}+3\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}} \right ] \nonumber \]
and
\[\left [ \hat{p_2}-3\sqrt{\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}, \hat{p_2}+3\sqrt{\frac{\hat{p_2}(1-\hat{p_2})}{n_2}} \right ] \nonumber \]
must lie wholly within the interval \([0,1]\).
Using the data of Example \(\PageIndex{1}\), test whether there is sufficient evidence to conclude that public web access to the inspection records has increased the proportion of projects that passed on the first inspection by more than \(5\) percentage points. Use the critical value approach at the \(10\%\) level of significance.
Solution
- Step 1. Taking into account the labeling of the populations an increase in passing rate at the first inspection by more than \(5\) percentage points after public access on the web may be expressed as \(p_2>p_1+0.05\), which by algebra is the same as \(p_1-p_2<-0.05\). This is the alternative hypothesis. Since the null hypothesis is always expressed as an equality, with the same number on the right as is in the alternative hypothesis, the test is
\[H_0: p_1-p_2=-0.05\\ \text{vs.}\\ H_a: p_1-p_2<-0.05\; \; @\; \; \alpha =0.10 \nonumber \]
- Step 2. Since the test is with respect to a difference in population proportions the test statistic is
\[Z=\frac{(\hat{p_1}-\hat{p_2})-D_0}{\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}} \nonumber \]
- Step 3. Inserting the values given in Example \(\PageIndex{1}\) and the value \(D_0=-0.05\)into the formula for the test statistic gives
\[Z=\frac{(\hat{p_1}-\hat{p_2})-D_0}{\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}}=\frac{(-0.13)-(-0.05)}{\sqrt{\frac{(0.67)(0.33)}{500}+\frac{(0.8)(0.2)}{100}}}=-1.770 \nonumber \]
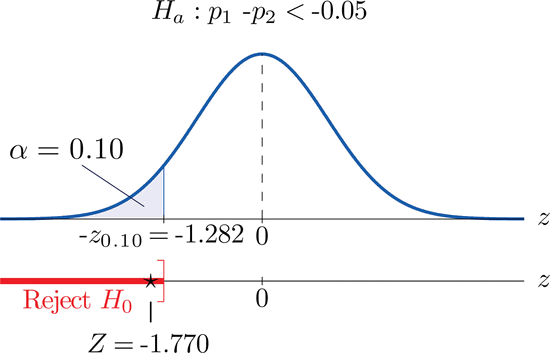
- Step 4. Since the symbol in \(H_a\) is “\(<\)” this is a left-tailed test, so there is a single critical value, \(z_\alpha =-z_{0.10}\). From the last row in Figure 7.1.6 \(z_{0.10}=1.282\), so \(-z_{0.10}=-1.282\). The rejection region is \((-\infty ,-1.282]\).
- Step 5. As shown in Figure \(\PageIndex{2}\) the test statistic falls in the rejection region. The decision is to reject \(H_0\). In the context of the problem our conclusion is:
The data provide sufficient evidence, at the \(10\%\) level of significance, to conclude that the rate of passing on the first inspection has increased by more than \(5\) percentage points since records were publicly posted on the web.
Perform the test of Example \(\PageIndex{2}\) using the \(p\)-value approach.
Solution
The first three steps are identical to those in Example \(\PageIndex{2}\)
- Step 4. Because the test is left-tailed the observed significance or \(p\)-value of the test is just the area of the left tail of the standard normal distribution that is cut off by the test statistic \(Z=-1.770\). From Figure 7.1.5 the area of the left tail determined by \(-1.77\) is \(0.0384\). The \(p\)-value is \(0.0384\).
- Step 5. Since the \(p\)-value \(0.0384\) is less than \(\alpha =0.10\), the decision is to reject the null hypothesis: The data provide sufficient evidence, at the \(10\%\) level of significance, to conclude that the rate of passing on the first inspection has increased by more than \(5\) percentage points since records were publicly posted on the web.
Finally a common misuse of the formulas given in this section must be mentioned. Suppose a large pre-election survey of potential voters is conducted. Each person surveyed is asked to express a preference between, say, Candidate \(A\) and Candidate \(B\). (Perhaps “no preference” or “other” are also choices, but that is not important.) In such a survey, estimators \(\hat{p}_A\) and \(\hat{p}B\) of \(p_A\) and \(p_B\) can be calculated. It is important to realize, however, that these two estimators were not calculated from two independent samples. While \(\hat{p}A−\hat{p}_B\) may be a reasonable estimator of \(p_A−p_B\), the formulas for confidence intervals and for the standardized test statistic given in this section are not valid for data obtained in this manner.
Key Takeaway
- A confidence interval for the difference in two population proportions is computed using a formula in the same fashion as was done for a single population mean.
- The same five-step procedure used to test hypotheses concerning a single population proportion is used to test hypotheses concerning the difference between two population proportions. The only difference is in the formula for the standardized test statistic.


