9.1: Comparison of Two Population Means- Large, Independent Samples
- Page ID
- 572
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To understand the logical framework for estimating the difference between the means of two distinct populations and performing tests of hypotheses concerning those means.
- To learn how to construct a confidence interval for the difference in the means of two distinct populations using large, independent samples.
- To learn how to perform a test of hypotheses concerning the difference between the means of two distinct populations using large, independent samples.
Suppose we wish to compare the means of two distinct populations. Figure \(\PageIndex{1}\) illustrates the conceptual framework of our investigation in this and the next section. Each population has a mean and a standard deviation. We arbitrarily label one population as Population \(1\) and the other as Population \(2\), and subscript the parameters with the numbers \(1\) and \(2\) to tell them apart. We draw a random sample from Population \(1\) and label the sample statistics it yields with the subscript \(1\). Without reference to the first sample we draw a sample from Population \(2\) and label its sample statistics with the subscript \(2\).
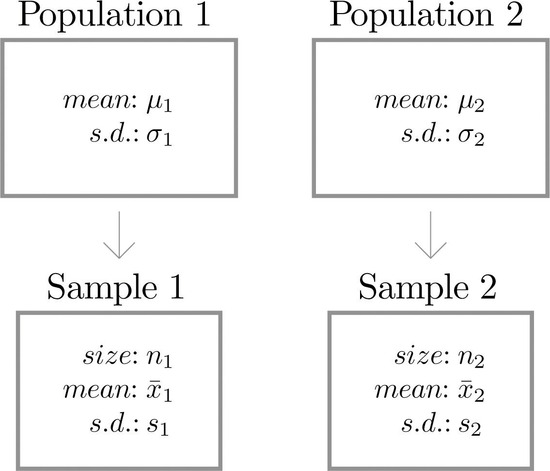
Samples from two distinct populations are independent if each one is drawn without reference to the other, and has no connection with the other.
Our goal is to use the information in the samples to estimate the difference \(\mu _1-\mu _2\) in the means of the two populations and to make statistically valid inferences about it.
Confidence Intervals
Since the mean \(x-1\) of the sample drawn from Population \(1\) is a good estimator of \(\mu _1\) and the mean \(x-2\) of the sample drawn from Population \(2\) is a good estimator of \(\mu _2\), a reasonable point estimate of the difference \(\mu _1-\mu _2\) is \(\bar{x_1}-\bar{x_2}\). In order to widen this point estimate into a confidence interval, we first suppose that both samples are large, that is, that both \(n_1\geq 30\) and \(n_2\geq 30\). If so, then the following formula for a confidence interval for \(\mu _1-\mu _2\) is valid. The symbols \(s_{1}^{2}\) and \(s_{2}^{2}\) denote the squares of \(s_1\) and \(s_2\). (In the relatively rare case that both population standard deviations \(\sigma _1\) and \(\sigma _2\) are known they would be used instead of the sample standard deviations.)
\(100(1-\alpha )\%\) Confidence Interval for the Difference Between Two Population Means: Large, Independent Samples
The samples must be independent, and each sample must be large:
To compare customer satisfaction levels of two competing cable television companies, \(174\) customers of Company \(1\) and \(355\) customers of Company \(2\) were randomly selected and were asked to rate their cable companies on a five-point scale, with \(1\) being least satisfied and \(5\) most satisfied. The survey results are summarized in the following table:
| Company 1 | Company 2 |
|---|---|
| \(n_1=174\) | \(n_2=355\) |
| \(x-1=3.51\) | \(x-2=3.24\) |
| \(s_1=0.51\) | \(s_2=0.52\) |
Construct a point estimate and a 99% confidence interval for \(\mu _1-\mu _2\), the difference in average satisfaction levels of customers of the two companies as measured on this five-point scale.
Solution
The point estimate of \(\mu _1-\mu _2\) is
\[\bar{x_1}-\bar{x_2}=3.51-3.24=0.27 \nonumber \]
In words, we estimate that the average customer satisfaction level for Company \(1\) is \(0.27\) points higher on this five-point scale than it is for Company \(2\).
To apply the formula for the confidence interval, proceed exactly as was done in Chapter 7. The \(99\%\) confidence level means that \(\alpha =1-0.99=0.01\) so that \(z_{\alpha /2}=z_{0.005}\). From Figure 7.1.6 "Critical Values of " we read directly that \(z_{0.005}=2.576\). Thus
\[(\bar{x_1}-\bar{x_2})\pm z_{\alpha /2}\sqrt{\frac{s_{1}^{2}}{n_1}+\frac{s_{2}^{2}}{n_2}}=0.27\pm 2.576\sqrt{\frac{0.51^{2}}{174}+\frac{0.52^{2}}{355}}=0.27\pm 0.12 \nonumber \]
We are \(99\%\) confident that the difference in the population means lies in the interval \([0.15,0.39]\), in the sense that in repeated sampling \(99\%\) of all intervals constructed from the sample data in this manner will contain \(\mu _1-\mu _2\). In the context of the problem we say we are \(99\%\) confident that the average level of customer satisfaction for Company \(1\) is between \(0.15\) and \(0.39\) points higher, on this five-point scale, than that for Company \(2\).
Hypothesis Testing
Hypotheses concerning the relative sizes of the means of two populations are tested using the same critical value and \(p\)-value procedures that were used in the case of a single population. All that is needed is to know how to express the null and alternative hypotheses and to know the formula for the standardized test statistic and the distribution that it follows.
The null and alternative hypotheses will always be expressed in terms of the difference of the two population means. Thus the null hypothesis will always be written
\[H_0: \mu _1-\mu _2=D_0 \nonumber \]
where \(D_0\) is a number that is deduced from the statement of the situation. As was the case with a single population the alternative hypothesis can take one of the three forms, with the same terminology:
| Form of Ha | Terminology |
|---|---|
| \(H_a: \mu _1-\mu _2<D_0\) | Left-tailed |
| \(H_a: \mu _1-\mu _2>D_0\) | Right-tailed |
| \(H_a: \mu _1-\mu _2\neq D_0\) | Two-tailed |
As long as the samples are independent and both are large the following formula for the standardized test statistic is valid, and it has the standard normal distribution. (In the relatively rare case that both population standard deviations \(\sigma _1\) and \(\sigma _2\) are known they would be used instead of the sample standard deviations.)
Standardized Test Statistic for Hypothesis Tests Concerning the Difference Between Two Population Means: Large, Independent Samples
\[Z=\frac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{\frac{s_{1}^{2}}{n_1}+\frac{s_{2}^{2}}{n_2}}} \nonumber \]
The test statistic has the standard normal distribution.
The samples must be independent, and each sample must be large: \(n_1\geq 30\) and \(n_2\geq 30\).
Refer to Example \(\PageIndex{1}\) concerning the mean satisfaction levels of customers of two competing cable television companies. Test at the \(1\%\) level of significance whether the data provide sufficient evidence to conclude that Company \(1\) has a higher mean satisfaction rating than does Company \(2\). Use the critical value approach.
Solution:
- Step 1. If the mean satisfaction levels \(\mu _1\) and \(\mu _2\) are the same then \(\mu _1=\mu _2\), but we always express the null hypothesis in terms of the difference between \(\mu _1\) and \(\mu _2\), hence \(H_0\) is \(\mu _1-\mu _2=0\). To say that the mean customer satisfaction for Company \(1\) is higher than that for Company \(2\) means that \(\mu _1>\mu _2\), which in terms of their difference is \(\mu _1-\mu _2>0\). The test is therefore
\[H_0: \mu _1-\mu _2=0 \nonumber \]
\[vs. \nonumber \]
\[H_a: \mu _1-\mu _2>0\; \; @\; \; \alpha =0.01 \nonumber \]
- Step 2. Since the samples are independent and both are large the test statistic is
\[Z=\frac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{\frac{s_{1}^{2}}{n_1}+\frac{s_{2}^{2}}{n_2}}} \nonumber \]
- Step 3. Inserting the data into the formula for the test statistic gives
\[Z=\frac{(\bar{x_1}-\bar{x_2})-D_0}{\sqrt{\frac{s_{1}^{2}}{n_1}+\frac{s_{2}^{2}}{n_2}}}=\frac{(3.51-3.24)-0}{\sqrt{\frac{0.51^{2}}{174}+\frac{0.52^{2}}{355}}}=5.684 \nonumber \]
- Step 4. Since the symbol in \(H_a\) is “\(>\)” this is a right-tailed test, so there is a single critical value, \(z_\alpha =z_{0.01}\), which from the last line in Figure 7.1.6 "Critical Values of " we read off as \(2.326\). The rejection region is \([2.326,\infty )\).
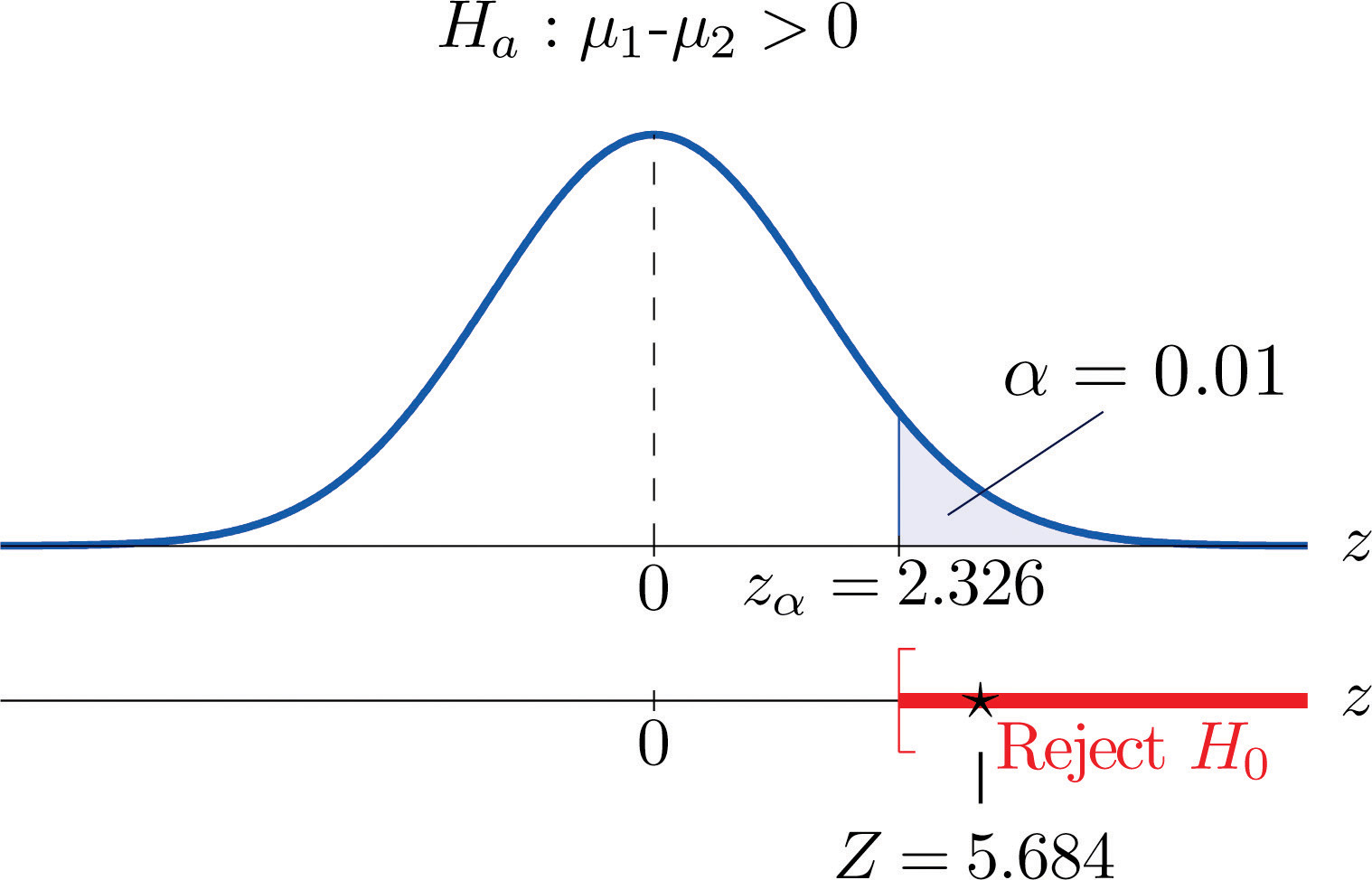
Figure \(\PageIndex{2}\): Rejection Region and Test Statistic for Example \(\PageIndex{2}\)
- Step 5. As shown in Figure \(\PageIndex{2}\) the test statistic falls in the rejection region. The decision is to reject \(H_0\). In the context of the problem our conclusion is:
The data provide sufficient evidence, at the \(1\%\) level of significance, to conclude that the mean customer satisfaction for Company \(1\) is higher than that for Company \(2\).
Perform the test of Example \(\PageIndex{2}\) using the \(p\)-value approach.
Solution:
The first three steps are identical to those in Example \(\PageIndex{2}\)
- Step 4. The observed significance or \(p\)-value of the test is the area of the right tail of the standard normal distribution that is cut off by the test statistic \(Z=5.684\). The number \(5.684\) is too large to appear in Figure 7.1.5, which means that the area of the left tail that it cuts off is \(1.0000\) to four decimal places. The area that we seek, the area of the right tail, is therefore \(1-1.0000=0.0000\) to four decimal places. See Figure \(\PageIndex{3}\). That is, \(p\)-value=\(0.0000\) to four decimal places. (The actual value is approximately \(0.000000007\).)
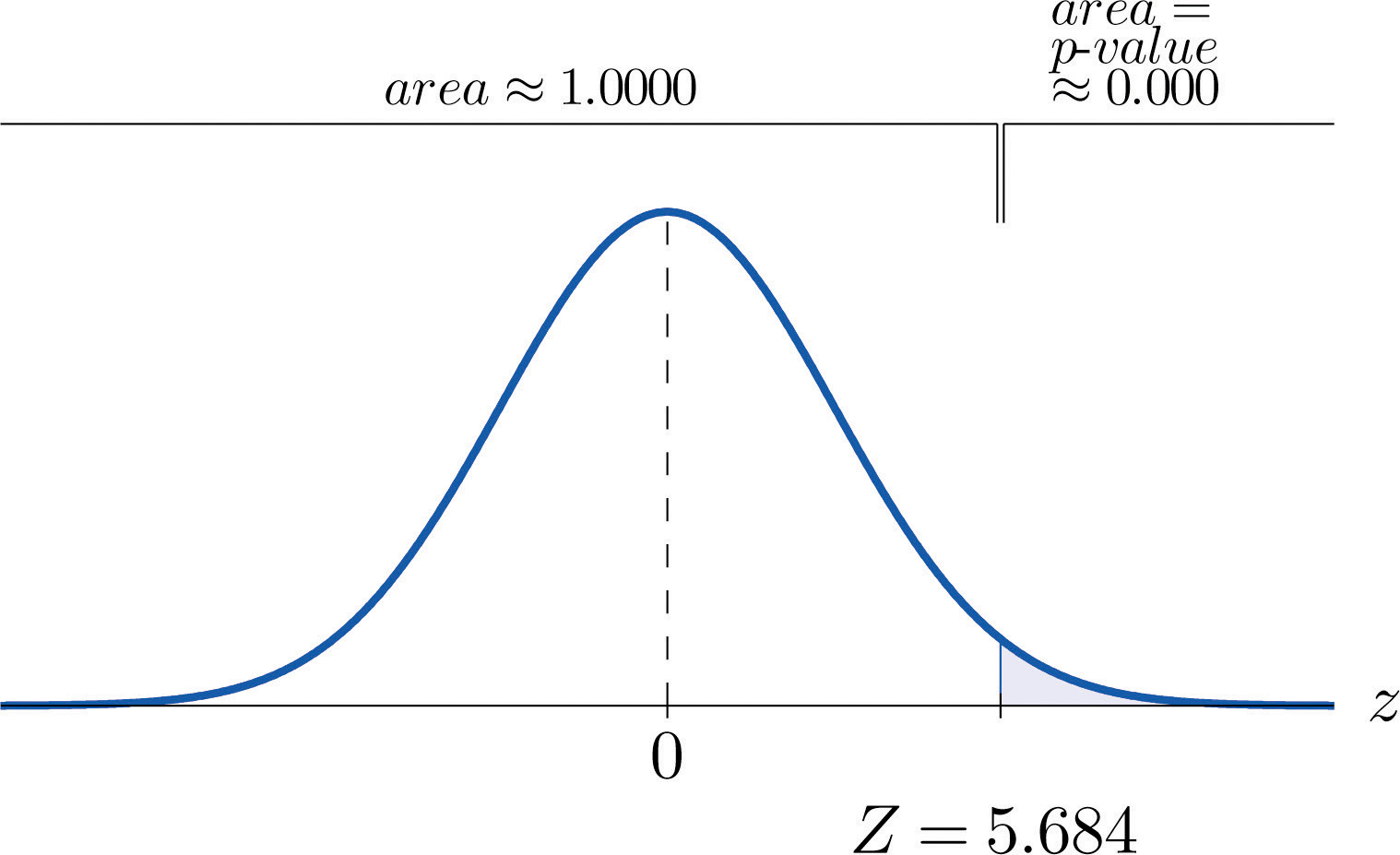
- Step 5. Since \(0.0000<0.01\), \(p-value <\alpha\) so the decision is to reject the null hypothesis:
The data provide sufficient evidence, at the \(1\%\) level of significance, to conclude that the mean customer satisfaction for Company \(1\) is higher than that for Company \(2\).
- A point estimate for the difference in two population means is simply the difference in the corresponding sample means.
- In the context of estimating or testing hypotheses concerning two population means, “large” samples means that both samples are large.
- A confidence interval for the difference in two population means is computed using a formula in the same fashion as was done for a single population mean.
- The same five-step procedure used to test hypotheses concerning a single population mean is used to test hypotheses concerning the difference between two population means. The only difference is in the formula for the standardized test statistic.


