8.2: Large Sample Tests for a Population Mean
- Page ID
- 520
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To learn how to apply the five-step test procedure for a test of hypotheses concerning a population mean when the sample size is large.
- To learn how to interpret the result of a test of hypotheses in the context of the original narrated situation.
In this section we describe and demonstrate the procedure for conducting a test of hypotheses about the mean of a population in the case that the sample size \(n\) is at least \(30\). The Central Limit Theorem states that \(\overline{X}\) is approximately normally distributed, and has mean \(\mu _{\overline{X}}=\mu\) and standard deviation \(\sigma _{\overline{X}}=\sigma /\sqrt{n}\), where \(\mu\) and \(\sigma\) are the mean and the standard deviation of the population. This implies that the statistic
\[\frac{\bar{x}-\mu }{\sigma /\sqrt{n}} \nonumber \]
has the standard normal distribution, which means that probabilities related to it are given in Figure 7.1.5 and the last line in Figure 7.1.6.
If we know \(\sigma\) then the statistic in the display is our test statistic. If, as is typically the case, we do not know \(\sigma\), then we replace it by the sample standard deviation \(s\). Since the sample is large the resulting test statistic still has a distribution that is approximately standard normal.
Standardized Test Statistics for Large Sample Hypothesis Tests Concerning a Single Population Mean
- If \(\sigma\) is known: \(Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}}\)
- If \(\sigma\) is unknown: \(Z=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}\)
The test statistic has the standard normal distribution.
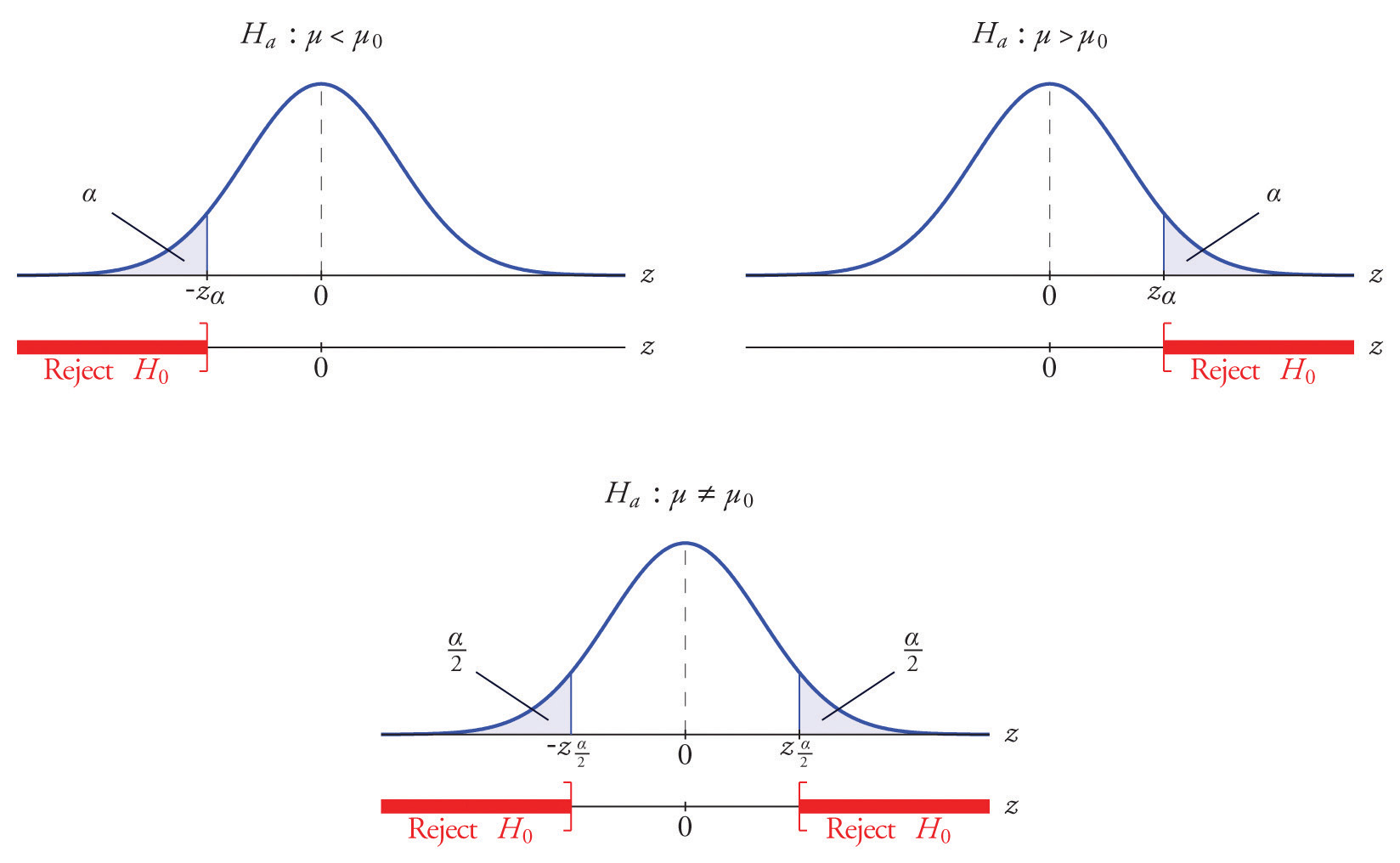
The distribution of the standardized test statistic and the corresponding rejection region for each form of the alternative hypothesis (left-tailed, right-tailed, or two-tailed), is shown in Figure \(\PageIndex{1}\).
It is hoped that a newly developed pain reliever will more quickly produce perceptible reduction in pain to patients after minor surgeries than a standard pain reliever. The standard pain reliever is known to bring relief in an average of \(3.5\) minutes with standard deviation \(2.1\) minutes. To test whether the new pain reliever works more quickly than the standard one, \(50\) patients with minor surgeries were given the new pain reliever and their times to relief were recorded. The experiment yielded sample mean \(\bar{x}=3.1\) minutes and sample standard deviation \(s=1.5\) minutes. Is there sufficient evidence in the sample to indicate, at the \(5\%\) level of significance, that the newly developed pain reliever does deliver perceptible relief more quickly?
Solution
We perform the test of hypotheses using the five-step procedure given at the end of Section 8.1.
- Step 1. The natural assumption is that the new drug is no better than the old one, but must be proved to be better. Thus if \(\mu\) denotes the average time until all patients who are given the new drug experience pain relief, the hypothesis test is \[H_0: \mu =3.5\\ \text{vs}\\ H_a:\mu <3.5\; @\; \alpha =0.05 \nonumber \]
- Step 2. The sample is large, but the population standard deviation is unknown (the \(2.1\) minutes pertains to the old drug, not the new one). Thus the test statistic is \[Z=\frac{\bar{x}-\mu _0}{s /\sqrt{n}} \nonumber \] and has the standard normal distribution.
- Step 3. Inserting the data into the formula for the test statistic gives \[Z=\frac{\bar{x}-\mu _0}{s /\sqrt{n}}=\frac{3.1-3.5}{1.5/\sqrt{50}}=-1.886 \nonumber \]
- Step 4. Since the symbol in \(H_a\) is “\(<\)” this is a left-tailed test, so there is a single critical value, \(-z_\alpha =-z_{0.005}\), which from the last line in Figure 7.1.6 we read off as \(-1.645\). The rejection region is \((-\infty ,-1.645]\).
- Step 5. As shown in Figure \(\PageIndex{2}\) the test statistic falls in the rejection region. The decision is to reject \(H_0\). In the context of the problem our conclusion is:
The data provide sufficient evidence, at the \(5\%\) level of significance, to conclude that the average time until patients experience perceptible relief from pain using the new pain reliever is smaller than the average time for the standard pain reliever.
.png?revision=1&size=bestfit&width=544&height=350)
A cosmetics company fills its best-selling \(8\) ounce jars of facial cream by an automatic dispensing machine. The machine is set to dispense a mean of \(8.1\) ounces per jar. Uncontrollable factors in the process can shift the mean away from \(8.1\) and cause either underfill or overfill, both of which are undesirable. In such a case the dispensing machine is stopped and recalibrated. Regardless of the mean amount dispensed, the standard deviation of the amount dispensed always has value \(0.22\) ounce. A quality control engineer routinely selects \(30\) jars from the assembly line to check the amounts filled. On one occasion, the sample mean is \(\bar{x}=8.2\) ounces and the sample standard deviation is \(s=0.25\) ounce. Determine if there is sufficient evidence in the sample to indicate, at the \(1\%\) level of significance, that the machine should be recalibrated.
Solution
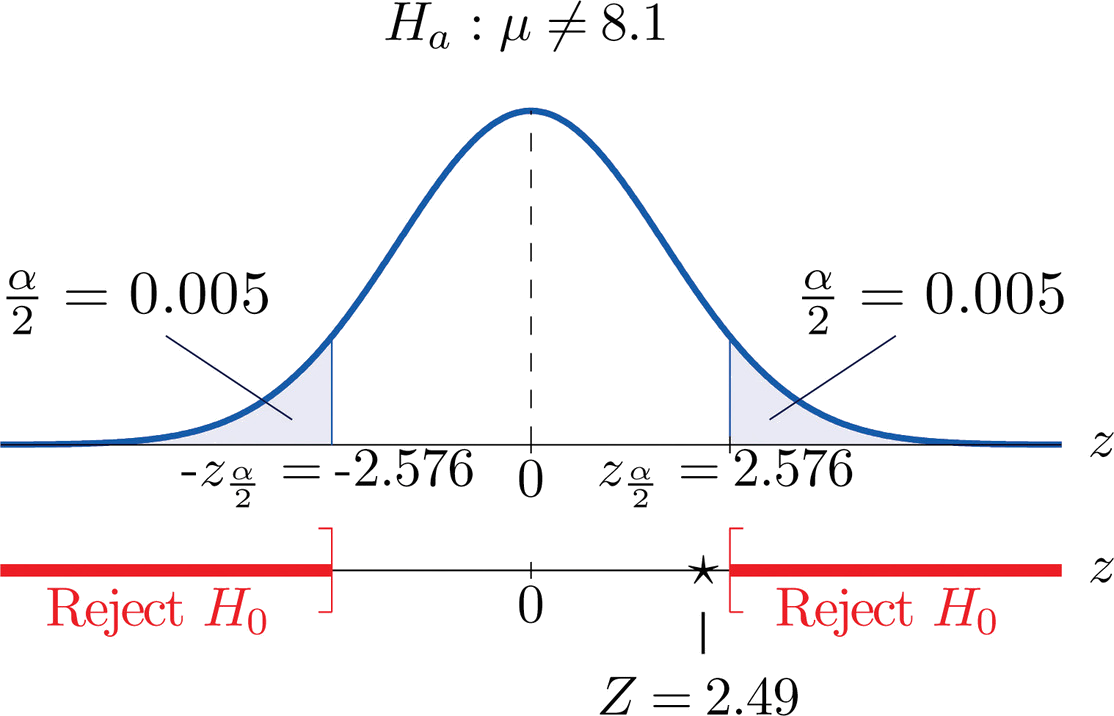
- Step 1. The natural assumption is that the machine is working properly. Thus if \(\mu\) denotes the mean amount of facial cream being dispensed, the hypothesis test is \[H_0: \mu =8.1\\ \text{vs}\\ H_a:\mu \neq 8.1\; @\; \alpha =0.01 \nonumber \]
- Step 2. The sample is large and the population standard deviation is known. Thus the test statistic is \[Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}} \nonumber \] and has the standard normal distribution.
- Step 3. Inserting the data into the formula for the test statistic gives \[Z=\frac{\bar{x}-\mu _0}{\sigma /\sqrt{n}}=\frac{8.2-8.1}{0.22/\sqrt{30}}=2.490 \nonumber \]
- Step 4. Since the symbol in \(H_a\) is “\(\neq\)” this is a two-tailed test, so there are two critical values, \(\pm z_{\alpha /2}=\pm z_{0.005}\), which from the last line in Figure 7.1.6 "Critical Values of " we read off as \(\pm 2.576\). The rejection region is \((-\infty ,-2.576]\cup [2.576,\infty )\).
- Step 5. As shown in Figure \(\PageIndex{3}\) the test statistic does not fall in the rejection region. The decision is not to reject \(H_0\). In the context of the problem our conclusion is:
The data do not provide sufficient evidence, at the \(1\%\) level of significance, to conclude that the average amount of product dispensed is different from \(8.1\) ounce. We conclude that the machine does not need to be recalibrated.
- There are two formulas for the test statistic in testing hypotheses about a population mean with large samples. Both test statistics follow the standard normal distribution.
- The population standard deviation is used if it is known, otherwise the sample standard deviation is used.
- The same five-step procedure is used with either test statistic.


