17.7: Chi Square (Exercises)
- Page ID
- 2515
General Questions
Q1
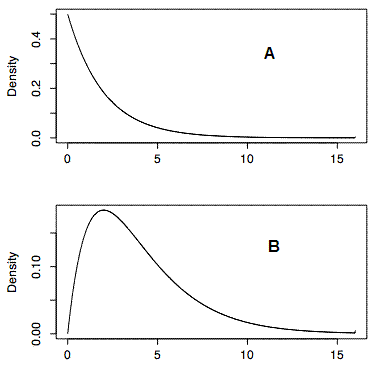
Which of the two Chi Square distributions shown below (\(A\) or \(B\)) has the larger degrees of freedom? How do you know? (relevant section)
Q2
Twelve subjects were each given two flavors of ice cream to taste and then were asked whether they liked them. Two of the subjects liked the first flavor and nine of them liked the second flavor. Is it valid to use the Chi Square test to determine whether this difference in proportions is significant? Why or why not? (relevant section)
Q3
A die is suspected of being biased. It is rolled \(25\) times with the following result:
|
Outcome
|
Frequency
|
|
1
|
9
|
|
2
|
4
|
|
3
|
1
|
|
4
|
8
|
|
5
|
3
|
|
6
|
0
|
Conduct a significance test to see if the die is biased.
- What Chi Square value do you get and how many degrees of freedom does it have?
- What is the \(p\) value? (relevant section)
Q4
A recent experiment investigated the relationship between smoking and urinary incontinence. Of the \(322\) subjects in the study who were incontinent, \(113\) were smokers, \(51\) were former smokers, and \(158\) had never smoked. Of the \(284\) control subjects who were not incontinent, \(68\) were smokers, \(23\) were former smokers, and \(193\) had never smoked.
- Create a table displaying this data.
- What is the expected frequency in each cell?
- Conduct a significance test to see if there is a relationship between smoking and incontinence. What Chi Square value do you get? What \(p\) value do you get?
- What do you conclude? (relevant section)
Q5
At a school pep rally, a group of sophomore students organized a free raffle for prizes. They claim that they put the names of all of the students in the school in the basket and that they randomly drew \(36\) names out of this basket. Of the prize winners, \(6\) were freshmen, \(14\) were sophomores, \(9\) were juniors, and \(7\) were seniors. The results do not seem that random to you. You think it is a little fishy that sophomores organized the raffle and also won the most prizes. Your school is composed of \(30\%\) freshmen, \(25\%\) sophomores, \(25\%\) juniors, and \(20\%\) seniors.
- What are the expected frequencies of winners from each class?
- Conduct a significance test to determine whether the winners of the prizes were distributed throughout the classes as would be expected based on the percentage of students in each group. Report your Chi Square and \(p\) values.
- What do you conclude? (relevant section)
Q6
Some parents of the West Bay little leaguers think that they are noticing a pattern. There seems to be a relationship between the number on the kids' jerseys and their position. These parents decide to record what they see. The hypothetical data appear below. Conduct a Chi Square test to determine if the parents' suspicion that there is a relationship between jersey number and position is right. Report your Chi Square and p values. (relevant section)
|
|
Infield
|
Outfield
|
Pitcher
|
Total
|
|
0-9
|
12
|
5
|
5
|
22
|
|
10-19
|
5
|
10
|
2
|
17
|
|
20+
|
4
|
4
|
7
|
15
|
|
Total
|
21
|
19
|
14
|
54
|
Q7
True/false: A Chi Square distribution with \(2\; df\) has a larger mean than a Chi Square distribution with \(12\; df\). (relevant section)
Q8
True/false: A Chi Square test is often used to determine if there is a significant relationship between two continuous variables. (relevant section)
Q9
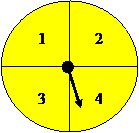
True/false: Imagine that you want to determine if the spinner shown below is biased. You spin it \(50\) times and write down how many times the arrow lands in each section. You will reject the null hypothesis at the \(0.05\) level and determine that this spinner is biased if you calculate a Chi Square value of \(7.82\) or higher. (relevant section)
Questions from Case Studies
The following question uses data from the SAT and GPA (SG) case study.
Q10
Answer these items to determine if the math SAT scores are normally distributed. You may want to first standardize the scores. (relevant section)
- If these data were normally distributed, how many scores would you expect there to be in each of these brackets:
- smaller than \(1\) \(SD\) below the mean
- in between the mean and \(1\) \(SD\) below the mean
- in between the mean and \(1\) \(SD\) above the mean
- greater than \(1\) \(SD\) above the mean?
- How many scores are actually in each of these brackets?
- Conduct a Chi Square test to determine if the math SAT scores are normally distributed based on these expected and observed frequencies. (relevant section)
The following questions are from the Diet and Health (DH) case study.
Q11
(DH#3) Conduct a Pearson Chi Square test to determine if there is any relationship between diet and outcome. Report the Chi Square and \(p\) values and state your conclusions. (relevant section)
The following questions are from ARTIST (reproduced with permission).

Q12
A study compared members of a medical clinic who filed complaints with a random sample of members who did not complain. The study divided the complainers into two subgroups: those who filed complaints about medical treatment and those who filed nonmedical complaints. Here are the data on the total number in each group and the number who voluntarily left the medical clinic. Set up a two-way table. Analyze these data to see if there is a relationship between complaint (no, yes - medical, yes - nonmedical) and leaving the clinic (yes or no).
| No Complaint | Medical Complaint | Non Medical Complaint | |
| Total | 743 | 199 | 440 |
| Left | 22 | 26 | 28 |
Q13
Imagine that you believe there is a relationship between a person's eye color and where he or she prefers to sit in a large lecture hall. You decide to collect data from a random sample of individuals and conduct a chi-square test of independence. What would your two-way table look like? Use the information to construct such a table, and be sure to label the different levels of each category.
Q14
A geologist collects hand-specimen sized pieces of limestone from a particular area. A qualitative assessment of both texture and color is made with the following results. Is there evidence of association between color and texture for these limestones? Explain your answer.
|
Color |
|||
|
Texture |
Light |
Medium |
Dark |
|
Fine |
4 |
20 |
8 |
|
Medium |
5 |
23 |
12 |
|
Coarse |
21 |
23 |
4 |
Q15
Suppose that college students are asked to identify their preferences in political affiliation (Democrat, Republican, or Independent) and in ice cream (chocolate, vanilla, or strawberry). Suppose that their responses are represented in the following two-way table (with some of the totals left for you to calculate).
| Chocolate | Vanilla | Strawberry | Total | |
| Democrat | 26 | 43 | 13 | 82 |
| Republican | 45 | 12 | 8 | 65 |
| Independent | 9 | 13 | 4 | |
| Total | 68 | 25 | 173 |
- What proportion of the respondents prefer chocolate ice cream?
- What proportion of the respondents are Independents?
- What proportion of Independents prefer chocolate ice cream?
- What proportion of those who prefer chocolate ice cream are Independents?
- Analyze the data to determine if there is a relationship between political party preference and ice cream preference.
Q16
NCAA collected data on graduation rates of athletes in Division I in the mid \(1980s\). Among \(2,332\) men, \(1,343\) had not graduated from college, and among \(959\) women, \(441\) had not graduated.
- Set up a two-way table to examine the relationship between gender and graduation.
- Identify a test procedure that would be appropriate for analyzing the relationship between gender and graduation. Carry out the procedure and state your conclusion.
Select Answers
S3
- \(\text{Chi Square} = 16.0\), \(df = 5\)
S4
- Incontinent/Smoker cell: \(96.2\)
S5
- \(p = 0.18\)
S6
\(\text{Chi Square} = 10.2\)
S10
-
- Scores smaller than \(1\) \(SD\) below the mean: \(24\)
S11
\(\text{Chi Square} = 16.6\)


