14.E: Regression (Exercises)
- Page ID
- 2650
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)General Questions
Q1
What is the equation for a regression line? What does each term in the line refer to? (relevant section)
Q2
The formula for a regression equation based on a sample size of \(25\) observations is \(Y' = 2X + 9\).
- What would be the predicted score for a person scoring \(6\) on \(X\)?
- If someone's predicted score was \(14\), what was this person's score on \(X\)? (relevant section)
Q3
What criterion is used for deciding which regression line fits best? (relevant section)
Q4
What does the standard error of the estimate measure? What is the formula for the standard error of the estimate? (relevant section)
Q5
- In a regression analysis, the sum of squares for the predicted scores is \(100\) and the sum of squares error is \(200\), what is \(R^2\)?
- In a different regression analysis, \(40\%\) of the variance was explained. The sum of squares total is \(1000\). What is the sum of squares of the predicted values? (relevant section)
Q6
For the \(X,Y\) data below, compute:
- \(r\) and determine if it is significantly different from zero.
- the slope of the regression line and test if it differs significantly from zero.
- the \(95\%\) confidence interval for the slope.
(relevant section)
|
X
|
Y
|
|
2
|
5
|
|
4
|
6
|
|
4
|
7
|
|
5
|
11
|
|
6
|
12
|
Q7
What assumptions are needed to calculate the various inferential statistics of linear regression? (relevant section)
Q8
The correlation between years of education and salary in a sample of \(20\) people from a certain company is \(0.4\). Is this correlation statistically significant at the \(0.05\) level? (relevant section)
Q9
A sample of \(X\) and \(Y\) scores is taken, and a regression line is used to predict \(Y\) from \(X\). If \(SSY' = 300\), \(SSE = 500\), and \(N = 50\), what is: (relevant section relevant section)
- \(SSY\)?
- the standard error of the estimate?
- \(R^2\)?
Q10
Using linear regression, find the predicted post-test score for someone with a score of \(43\) on the pre-test. (relevant section)
| Pre | Post |
| 59 | 56 |
| 52 | 63 |
| 44 | 55 |
| 51 | 50 |
| 42 | 66 |
| 42 | 48 |
| 41 | 58 |
| 45 | 36 |
| 27 | 13 |
| 63 | 50 |
| 54 | 81 |
| 44 | 56 |
| 50 | 64 |
| 47 | 50 |
| 55 | 63 |
| 49 | 57 |
| 45 | 73 |
| 57 | 63 |
| 46 | 46 |
| 60 | 60 |
| 65 | 47 |
| 64 | 73 |
| 50 | 58 |
| 74 | 85 |
| 59 | 44 |
Q11
The equation for a regression line predicting the number of hours of TV watched by children (\(Y\)) from the number of hours of TV watched by their parents (\(X\)) is \(Y' = 4 + 1.2X\). The sample size is \(12\).
- If the standard error of \(b\) is \(0.4\), is the slope statistically significant at the \(0.05\) level? (relevant section)
- If the mean of \(X\) is \(8\), what is the mean of \(Y\)? (relevant section)
Q12
Based on the table below, compute the regression line that predicts \(Y\) from \(X\). (relevant section)
|
MX
|
MY
|
sX | sY | r |
| 10 |
12
|
2.5 | 3.0 | -0.6 |
Q13
Does \(A\) or \(B\) have a larger standard error of the estimate? (relevant section)
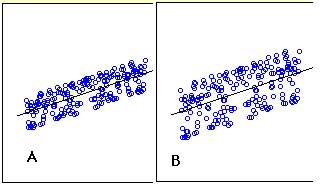
Q14
True/false: If the slope of a simple linear regression line is statistically significant, then the correlation will also always be significant. (relevant section)
Q15
True/false: If the slope of the relationship between \(X\) and \(Y\) is larger for \(\text{Population 1}\) than for \(\text{Population 2}\), the correlation will necessarily be larger in \(\text{Population 1}\) than in \(\text{Population 1}\). Why or why not? (relevant section)
Q16
True/false: If the correlation is \(0.8\), then \(40\%\) of the variance is explained. (relevant section)
Q17
True/false: If the actual \(Y\) score was \(31\), but the predicted score was \(28\), then the error of prediction is \(3\). (relevant section)
Questions from Case Studies
The following question is from the Angry Moods (AM) case study.
Q18
(AM#23) Find the regression line for predicting Anger-Out from Control-Out.
- What is the slope?
- What is the intercept?
- Is the relationship at least approximately linear?
- Test to see if the slope is significantly different from \(0\).
- What is the standard error of the estimate?
(relevant section, relevant section, relevant section)
The following question is from the SAT and GPA (SG) case study.
Q19
(SG#3) Find the regression line for predicting the overall university GPA from the high school GPA.
- What is the slope?
- What is the \(y\)-intercept?
- If someone had a \(2.2\) GPA in high school, what is the best estimate of his or her college GPA?
- If someone had a \(4.0\) GPA in high school, what is the best estimate of his or her college GPA?
(relevant section)
The following questions are from the Driving (D) case study.
Q20
(D#5) What is the correlation between age and how often the person chooses to drive in inclement weather? Is this correlation statistically significant at the \(0.01\) level? Are older people more or less likely to report that they drive in inclement weather? (relevant section, relevant section )
Q21
(D#8) What is the correlation between how often a person chooses to drive in inclement weather and the percentage of accidents the person believes occur in inclement weather? Is this correlation significantly different from \(0\)? (relevant section, relevant section )
Q22
(D#10) Use linear regression to predict how often someone rides public transportation in inclement weather from what percentage of accidents that person thinks occur in inclement weather. (Pubtran by Accident)
- Create a scatter plot of this data and add a regression line.
- What is the slope?
- What is the intercept?
- Is the relationship at least approximately linear?
- Test if the slope is significantly different from \(0\).
- Comment on possible assumption violations for the test of the slope.
- What is the standard error of the estimate?
(relevant section, relevant section, relevant section)
Selected Answers
S2
- \(21\)
S5
- \(0.33\)
S6
- \(b = 1.91\)
S9
- \(800\)
S12
\(a = 19.2\)
S18
- \(3.45\)
S19
- \(2.6\)
S20
\(r = 0.43\)
S22
- \(0.35\)


