27.1: Linear Regression (Section 26.1)
- Page ID
- 8858
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
To perform linear regression in R, we use the lm() function. Let’s generate some data and use this function to compute the linear regression solution.
npoints <- 100
intercept = 10
# slope of X/Y relationship
slope=0.5
# this lets us control the strength of the relationship
# by varying the amount of noise added to the y variable
noise_sd = 0.6
regression_data <- tibble(x = rnorm(npoints)) %>%
mutate(y = x*slope + rnorm(npoints)*noise_sd + intercept)
ggplot(regression_data,aes(x,y)) +
geom_point()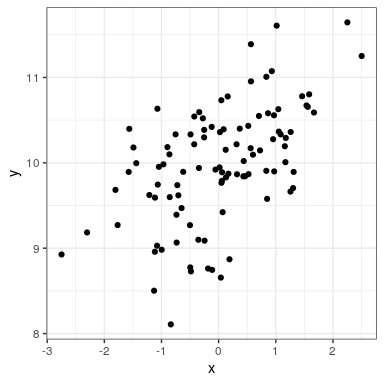
We can then apply lm() to these data:
lm_result <- lm(y ~ x, data=regression_data)
summary(lm_result)##
## Call:
## lm(formula = y ~ x, data = regression_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.5563 -0.3042 -0.0059 0.3804 1.2522
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.9761 0.0580 172.12 < 2e-16 ***
## x 0.3725 0.0586 6.35 6.6e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.58 on 98 degrees of freedom
## Multiple R-squared: 0.292, Adjusted R-squared: 0.284
## F-statistic: 40.4 on 1 and 98 DF, p-value: 6.65e-09We should see three things in the lm() results:
- The estimate of the Intercept in the model should be very close to the intercept that we specified
- The estimate for the x parameter should be very close to the slope that we specified
- The residual standard error should be roughly similar to the noise standard deviation that we specified


