4.3: The Binomial Distribution
- Page ID
- 562
- To learn the concept of a binomial random variable.
- To learn how to recognize a random variable as being a binomial random variable.
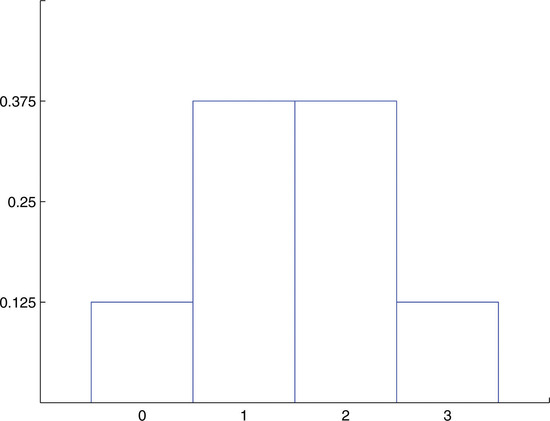
The experiment of tossing a fair coin three times and the experiment of observing the genders according to birth order of the children in a randomly selected three-child family are completely different, but the random variables that count the number of heads in the coin toss and the number of boys in the family (assuming the two genders are equally likely) are the same random variable, the one with probability distribution
\[\begin{array}{c|cccc} x& 0& 1& 2& 3\\ \hline P(x)& 0.125& 0.375& 0.375& 0.125\\ \end{array} \nonumber \]
A histogram that graphically illustrates this probability distribution is given in Figure \(\PageIndex{1}\). What is common to the two experiments is that we perform three identical and independent trials of the same action, each trial has only two outcomes (heads or tails, boy or girl), and the probability of success is the same number, \(0.5\), on every trial. The random variable that is generated is called the binomial random variable with parameters \(n=3\) and \(p=0.5\). This is just one case of a general situation.
Suppose a random experiment has the following characteristics.
- There are \(n\) identical and independent trials of a common procedure.
- There are exactly two possible outcomes for each trial, one termed “success” and the other “failure.”
- The probability of success on any one trial is the same number \(p\).
Then the discrete random variable \(X\) that counts the number of successes in the n trials is the binomial random variable with parameters \(n\) and \(p\). We also say that \(X\) has a binomial distribution with parameters \(n\) and \(p\).
The following four examples illustrate the definition. Note how in every case “success” is the outcome that is counted, not the outcome that we prefer or think is better in some sense.
- A random sample of \(125\) students is selected from a large college in which the proportion of students who are females is \(57\%\). Suppose \(X\) denotes the number of female students in the sample. In this situation there are \(n=125\) identical and independent trials of a common procedure, selecting a student at random; there are exactly two possible outcomes for each trial, “success” (what we are counting, that the student be female) and “failure;” and finally the probability of success on any one trial is the same number \(p = 0.57\). \(X\) is a binomial random variable with parameters \(n = 125\) and \(p = 0.57\).
- A multiple-choice test has \(15\) questions, each of which has five choices. An unprepared student taking the test answers each of the questions completely randomly by choosing an arbitrary answer from the five provided. Suppose \(X\) denotes the number of answers that the student gets right. \(X\) is a binomial random variable with parameters \(n = 15\) and \(p=1/5=0.20\).
- In a survey of \(1,000\) registered voters each voter is asked if he intends to vote for a candidate Titania Queen in the upcoming election. Suppose \(X\) denotes the number of voters in the survey who intend to vote for Titania Queen. \(X\) is a binomial random variable with \(n = 1000\) and \(p\) equal to the true proportion of voters (surveyed or not) who intend to vote for Titania Queen.
- An experimental medication was given to \(30\) patients with a certain medical condition. Suppose \(X\) denotes the number of patients who develop severe side effects. \(X\) is a binomial random variable with \(n = 30\) and \(p\) equal to the true probability that a patient with the underlying condition will experience severe side effects if given that medication.
Probability Formula for a Binomial Random Variable
Often the most difficult aspect of working a problem that involves the binomial random variable is recognizing that the random variable in question has a binomial distribution. Once that is known, probabilities can be computed using the following formula.
If \(X\) is a binomial random variable with parameters \(n\) and \(p\), then
\[P(x)=\dfrac{n!}{x!(n−x)!}p^xq^{n−x} \nonumber \]where \(q=1-p\) and where for any counting number \(m\), \(m!\) (read “m factorial”) is defined by
\[0!=1,1!=1,2!=1⋅2,3!=1⋅2⋅3 \nonumber \]and in general
\[m!=1⋅2 ⋅ ⋅ ⋅ (m−1)⋅m \nonumber \]Seventeen percent of victims of financial fraud know the perpetrator of the fraud personally.
- Use the formula to construct the probability distribution for the number \(X\) of people in a random sample of five victims of financial fraud who knew the perpetrator personally.
- A investigator examines five cases of financial fraud every day. Find the most frequent number of cases each day in which the victim knew the perpetrator.
- A investigator examines five cases of financial fraud every day. Find the average number of cases per day in which the victim knew the perpetrator.
Solution
The random variable X is binomial with parameters \(n = 5\) and \(p = 0.17\); \(q=1-p=0.83\). The possible values of \(X\) are \(0, 1, 2, 3, 4,\; \text{and}\; 5\).
\[\begin{align*} P(0) &= \frac{5!}{0!5!}(0.17)^0(0.83)^5\\ &= \frac{1\cdot 2\cdot 3\cdot 4\cdot 5}{(1)(1\cdot 2\cdot 3\cdot 4\cdot 5)}1\cdot (0.3939040643)\\ &= 0.3939040643\approx 0.3939 \end{align*} \nonumber \]
\[\begin{align*} P(1) &= \frac{5!}{1!4!}(0.17)^1(0.83)^4\\ &= \frac{1\cdot 2\cdot 3\cdot 4\cdot 5}{(1)(1\cdot 2\cdot 3\cdot 4)}(0.17)\cdot (0.47458321)\\ &= 5\cdot (0.17)\cdot (0.47458321)\\ &= 0.4033957285 \approx 0.4034 \end{align*} \nonumber \]
\[\begin{align*} P(2) &= \frac{5!}{2!3!}(0.17)^2(0.83)^3\\ &= \frac{1\cdot 2\cdot 3\cdot 4\cdot 5}{(1\cdot 2)(1\cdot 2\cdot 3)}(0.0289)\cdot (0.571787)\\ &= 10\cdot (0.0289)\cdot (0.571787)\\ &= 0.165246443 \approx 0.1652 \end{align*} \nonumber \]
\[\begin{array}{c|cccccc} x& 0& 1& 2& 3& 4& 5\\ \hline P(x)& 0.3939& 0.4034& 0.1652& 0.0338& 0.0035& 0.0001 \\ \end{array} \nonumber \]
The probabilities do not add up to exactly \(1\) because of rounding.
This probability distribution is represented by the histogram in Figure \(\PageIndex{2}\), which graphically illustrates just how improbable the events \(X = 4\) and \(X = 5\) are. The corresponding bar in the histogram above the number \(4\) is barely visible, if visible at all, and the bar above \(5\) is far too short to be visible.
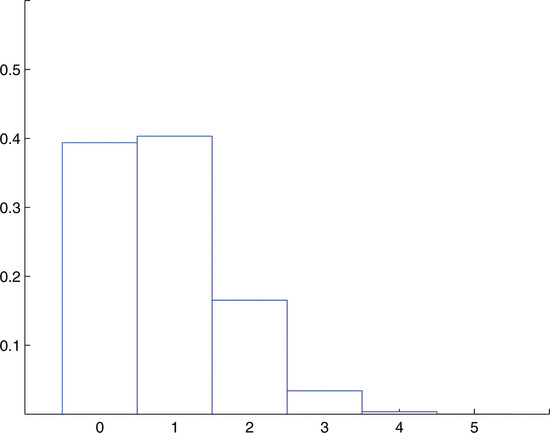
The value of \(X\) that is most likely is \(X = 1\), so the most frequent number of cases seen each day in which the victim knew the perpetrator is one.
The average number of cases per day in which the victim knew the perpetrator is the mean of \(X\), which is
\[\begin{align} μ&=\sum xP(x) \\ &=0⋅0.3939+1⋅0.4034+2⋅0.1652+3⋅0.0338+4⋅0.0035+5⋅0.0001 \\ &= 0.8497 \end{align} \nonumber \]
Special Formulas for the Mean and Standard Deviation of a Binomial Random Variable
Since a binomial random variable is a discrete random variable, the formulas for its mean, variance, and standard deviation given in the previous section apply to it, as we just saw in Example \(\PageIndex{2}\) in the case of the mean. However, for the binomial random variable there are much simpler formulas.
If \(X\) is a binomial random variable with parameters \(n\) and \(p\), then
\[\mu=np \nonumber \]
\[\sigma ^2=npq \nonumber \]
\[\sigma =\sqrt{npq} \nonumber \]
where \( q=1-p\).
Find the mean and standard deviation of the random variable \(X\) of Example \(\PageIndex{1}\).
Solution
The random variable \(X\) is binomial with parameters \(n = 5\) and \(p = 0.17\), and \(q=1-p=0.83\). Thus its mean and standard deviation are
\[\mu =np=(5)\cdot (0.17)=0.85 \; \; \text{(exactly)} \nonumber \]
and
\[\sigma =\sqrt{npq}=\sqrt{(5)\cdot (0.17)\cdot (0.83)}=\sqrt{0.7055}\approx 0.8399 \nonumber \]
The Cumulative Probability Distribution of a Binomial Random Variable
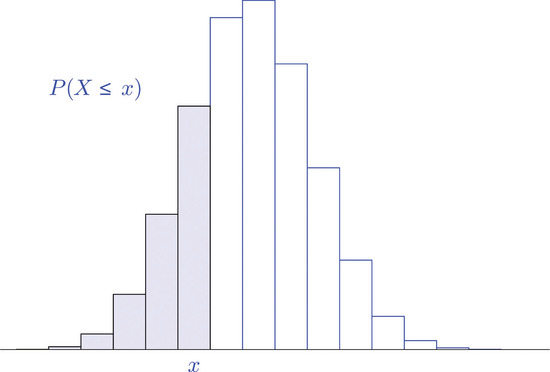
In order to allow a broader range of more realistic problems contains probability tables for binomial random variables for various choices of the parameters \(n\) and \(p\). These tables are not the probability distributions that we have seen so far, but are cumulative probability distributions. In the place of the probability \(P(x)\) the table contains the probability
\[P(X≤x) = P(0) + P(1) + \ldots + P(x) \nonumber \]
This is illustrated in Figure \(\PageIndex{3}\). The probability entered in the table corresponds to the area of the shaded region. The reason for providing a cumulative table is that in practical problems that involve a binomial random variable typically the probability that is sought is of the form \( P(X≤x)\) or \( P(X≥x)\). The cumulative table is much easier to use for computing \( P(X≤x)\) since all the individual probabilities have already been computed and added. The one table suffices for both \( P(X≤x)\) or \( P(X≥x)\) and can be used to readily obtain probabilities of the form \( P(x)\), too, because of the following formulas. The first is just the Probability Rule for Complements.
If \(X\) is a discrete random variable, then
\[P(X≥x)=1−P(X≤x−1) \nonumber \]
and
\[P(x)=P(X≤x)−P(X≤x−1) \nonumber \]
A student takes a ten-question true/false exam.
- Find the probability that the student gets exactly six of the questions right simply by guessing the answer on every question.
- Find the probability that the student will obtain a passing grade of \(60\%\) or greater simply by guessing.
Solution
Let \(X\) denote the number of questions that the student guesses correctly. Then \(X\) is a binomial random variable with parameters \(n = 10\) and \(p= 0.50\).
- The probability sought is \(P(6)\). The formula gives \[P(6)=10!(6!)(4!)(.5)6.54=0.205078125\nonumber \] Using the table, \[P(6)=P(X≤6)−P(X≤5)=0.8281−0.6230=0.2051\nonumber \]
- The student must guess correctly on at least \(60\%\) of the questions, which is \((0.60)\cdot (10)=6\) questions. The probability sought is not \(P(6)\) (an easy mistake to make), but \[P(X≥6)=P(6)+P(7)+P(8)+P(9)+P(10)\nonumber \] Instead of computing each of these five numbers using the formula and adding them we can use the table to obtain \[P(X≥6)=1−P(X≤5)=1−0.6230=0.3770\nonumber \] which is much less work and of sufficient accuracy for the situation at hand.
An appliance repairman services five washing machines on site each day. One-third of the service calls require installation of a particular part.
- The repairman has only one such part on his truck today. Find the probability that the one part will be enough today, that is, that at most one washing machine he services will require installation of this particular part.
- Find the minimum number of such parts he should take with him each day in order that the probability that he have enough for the day's service calls is at least \(95\%\).
Solution
Let \(X\) denote the number of service calls today on which the part is required. Then \(X\) is a binomial random variable with parameters \(n = 5\) and \(p=1/3=0.\bar{3}\)
- Note that the probability in question is not \(P(1)\), but rather \(P(X\leq 1)\). Using the cumulative distribution table, \[P(X≤1)=0.4609\nonumber \]
- The answer is the smallest number \(x\) such that the table entry \(P(X\leq x)\) is at least \(0.9500\). Since \(P(X\leq2 )=0.7901\) is less than \(0.95\), two parts are not enough. Since \(P(X\leq 3)=0.9547 \) is as large as \(0.95\), three parts will suffice at least \(95\%\) of the time. Thus the minimum needed is three.
Summary
- The discrete random variable \(X\) that counts the number of successes in \(n\) identical, independent trials of a procedure that always results in either of two outcomes, “success” or “failure,” and in which the probability of success on each trial is the same number \(p\), is called the binomial random variable with parameters \(n\) and \(p\).
- There is a formula for the probability that the binomial random variable with parameters \(n\) and \(p\) will take a particular value \(x\).
- There are special formulas for the mean, variance, and standard deviation of the binomial random variable with parameters \(n\) and \(p\) that are much simpler than the general formulas that apply to all discrete random variables.
- Cumulative probability distribution tables, when available, facilitate computation of probabilities encountered in typical practical situations.


