4.2: Values of the Pearson Correlation
- Page ID
- 2097
Learning Objectives
- Describe what Pearson's correlation measures
- Give the symbols for Pearson's correlation in the sample and in the population
- State the possible range for Pearson's correlation
- Identify a perfect linear relationship
The Pearson product-moment correlation coefficient is a measure of the strength of the linear relationship between two variables. It is referred to as Pearson's correlation or simply as the correlation coefficient. If the relationship between the variables is not linear, then the correlation coefficient does not adequately represent the strength of the relationship between the variables.
The symbol for Pearson's correlation is "\(ρ\)" when it is measured in the population and "\(r\)" when it is measured in a sample. Because we will be dealing almost exclusively with samples, we will use \(r\) to represent Pearson's correlation unless otherwise noted.
Pearson's \(r\) can range from \(-1\) to \(1\). An \(r\) of \(-1\) indicates a perfect negative linear relationship between variables, an \(r\) of \(0\) indicates no linear relationship between variables, and an \(r\) of \(1\) indicates a perfect positive linear relationship between variables. Figure \(\PageIndex{1}\) shows a scatter plot for which \(r = 1\).
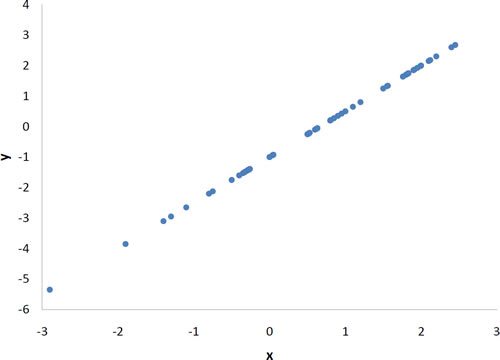
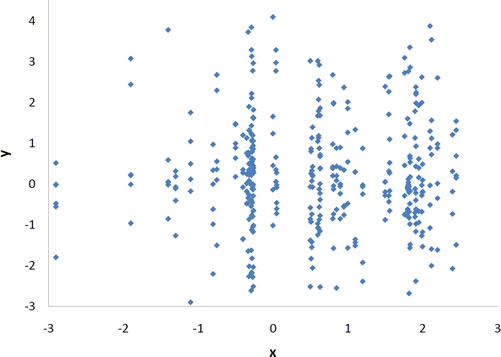
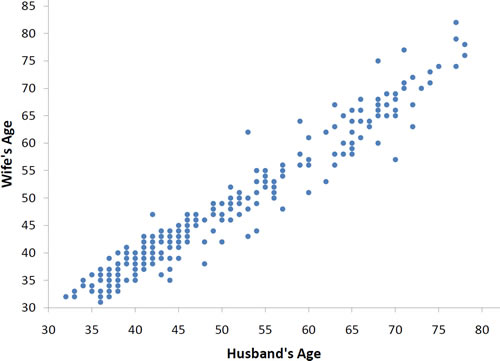
With real data, you would not expect to get values of \(r\) of exactly \(-1, 0,\: or\; 1\). The data for spousal ages shown in Figure \(\PageIndex{4}\) and described in the introductory section has an \(r\) of \(0.97\).
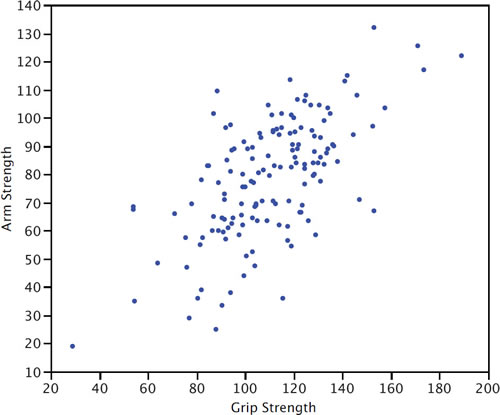
The relationship between grip strength and arm strength depicted in Figure \(\PageIndex{5}\) (also described in the introductory section) is \(0.63\).


