3.13: Variability Demo
- Page ID
- 2307
Learning Objectives
- Identify differences in the means and standard deviations of distributions
Instructions
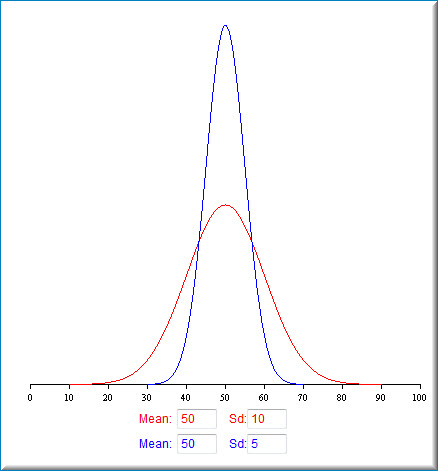
The demonstration shows a graph of two normal distributions. Both distributions have means of \(50\). The red distribution has a standard deviation of \(10\); the blue distribution has a standard deviation of \(5\). You can see that the red distribution is more spread out than the blue distribution. Note that about two thirds of the area of the distributions is within one standard deviation of the mean. For the red distribution, this is between \(40\) and \(60\); for the blue distribution, this is between \(45\) and \(55\). About \(95\%\) of a normal distribution is within two standard deviations from the mean. For the red distribution, this is between \(30\) and \(70\); for the blue it is between \(40\) and \(60\).
You can change the means and standard deviations of the distributions and see the results visually. For some values, the distributions will be off the graph. For example, if you give a distribution a mean of \(200\), it will not be shown.
Illustrated Instructions
The demonstration starts with \(2\) normal distributions with equal means and different standard deviations (see screenshot below).
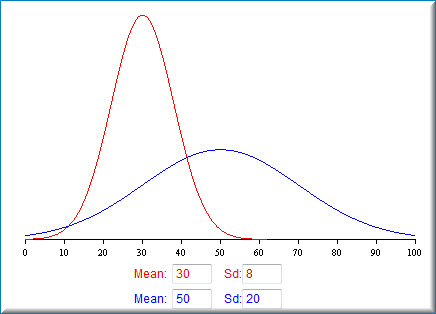
The means and standard deviations for both distributions can be changed and these changes will be reflected in the graph. The screenshot below shows the distributions with different means and standard deviations.