10.9: Confidence Interval Simulation
- Page ID
- 2631
Learning Objectives
- Develop a basic understanding of the properties of a sampling distribution based on the properties of the population
Instructions
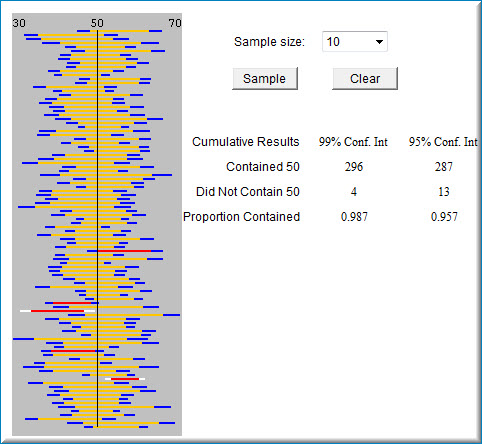
This simulation illustrates confidence intervals. For each run of the simulation, \(100\) sample experiments are conducted and a confidence interval on the mean is computed for each experiment. In each experiment, scores are sampled from a population with a mean of \(50\) and a standard deviation of \(10\). Therefore the parameter being estimated is always \(50\). Both \(95\%\) and \(99\%\) confidence intervals are computed for each experiment. If the \(95\%\) confidence interval contains the population mean of \(50\), then the confidence interval is shown as an orange line. If the interval does not contain \(50\), it is shown as a red line. The \(99\%\) confidence intervals are shown by extending the \(95\%\) intervals. The extension is in blue if the \(99\%\) interval contains \(50\) and in white if it does not. You can choose to make the sample size for each experiment \(10\), \(15\), or \(20\). One hundred simulated experiments are conducted when you click the "Sample" button. The cumulative results are shown at the bottom of the display. You can reset the cumulative results by clicking the "Clear" button.
Illustrated Instructions
The demonstration generates confidence intervals for sample experiments taken from a population with a mean of \(50\) and a standard deviation of \(10\). You can choose from various sample sizes but as can be seen from the figure below the default size is \(10\). Each time you click the sample button confidence intervals for \(100\) experiments are generated and displayed on the graph on the left.
The figure below displays the results of \(300\) experiments with a sample size of \(10\). The \(95\%\) confidence intervals that contain the mean of \(50\) are shown in orange and the those that do not are shown in red. The \(99\%\) confidence intervals are shown in blue if they contain \(50\) and white if they do not.