3.1: Introduction to Autoregressive Moving Average (ARMA) Processes
- Page ID
- 860
In this chapter autoregressive moving average processes are discussed. They play a crucial role in specifying time series models for applications. As the solutions of stochastic difference equations with constant coefficients and these processes possess a linear structure.
Definition 3.1.1: ARMA processes
(a) A weakly stationary process \(X_t\colon t\in\mathbb{Z}\) is called an autoregressive moving average time series of order \(p,q\), abbreviated by \(ARMA(p,q)\), if it satisfies the difference equations
\[\begin{equation}\label{eq:3.1.1}
X_t=\phi_1X_{t-1}+\ldots+\phi_pX_{t-p}+Z_t+\theta_1Z_{t-1}+\ldots+\theta_qZ_{t-q},
\qquad
t\in\mathbb{Z},
\end{equation} \tag{3.1.1} \]
where \(\phi_1,\ldots,\phi_p\) and \(\theta_1,\ldots,\theta_q\) are real constants, \(\phi_p\not=0\not=\theta_q\), and \((Z_t\colon t\in\mathbb{Z})\sim{\rm WN}(0,\sigma^2)\).
(b) A weakly stationary stochastic process \(X_t\colon t\in\mathbb{Z}\) is called an \(ARMA(p,q)\) time series with mean \(\mu\) if the process \(X_t-\mu\colon t\in\mathbb{Z}\) satisfies the equation system.
A more concise representation of Equation \ref{eq:3.1.1} can be obtained with the use of the backshift operator \(B\). To this end, define the autoregressive polynomial and the moving average polynomial by
\[ \phi(z)=1-\phi_1z-\phi_2z^2-\ldots-\phi_pz^p,\qquad z\in\mathbb{C}, \nonumber \]
and
\[ \theta(z)=1+\theta_1z+\theta_2z^2+\ldots+\theta_qz^q,\qquad z\in\mathbb{C}, \nonumber \]
respectively, where \(\mathbb{C}\) denotes the set of complex numbers. Inserting the backshift operator into these polynomials, the equations in (3.1.1) become
\[\begin{equation}\label{eq:3.1.2}
\phi(B)X_t=\theta(B)Z_t,\qquad t\in\mathbb{Z}.
\end{equation}\tag{3.1.2} \]
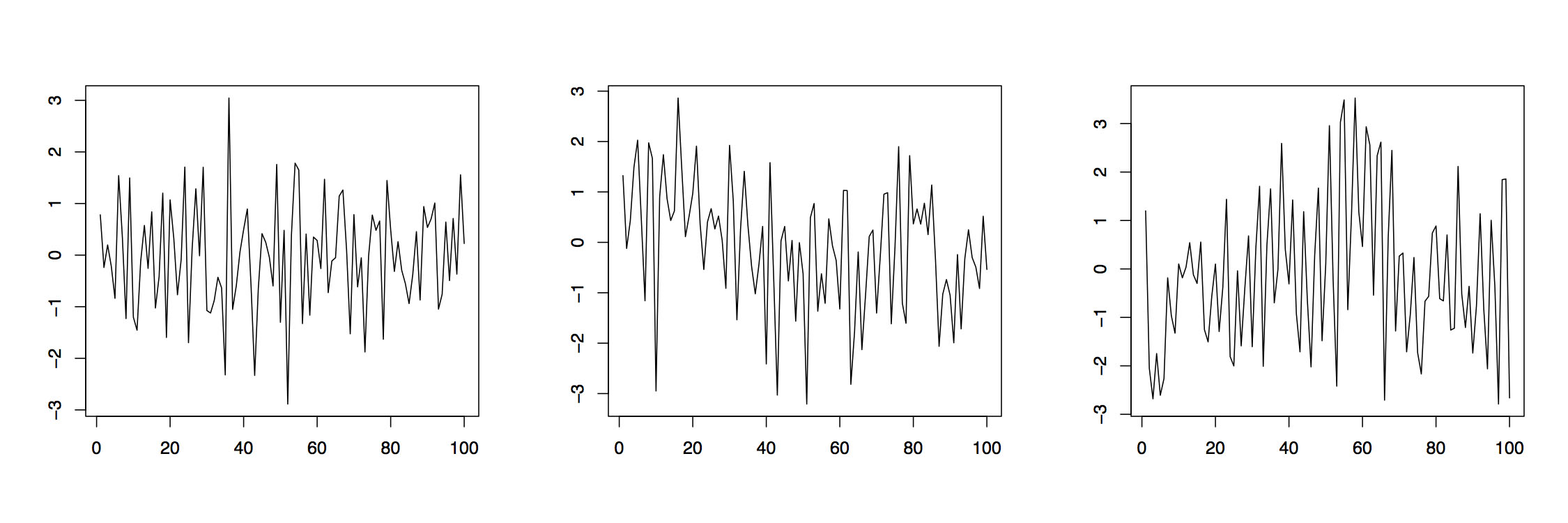
Example 3.1.1 Figure 3.1 displays realizations of three different autoregressive moving average time series based on independent, standard normally distributed \((Z_t\colon t\in\mathbb{Z})\). The left panel is an ARMA(2,2) process with parameter specifications \(\phi_1=.2\), \(\phi_2=-.3\), \(\theta_1=-.5\) and \(\theta_2=.3\). The middle plot is obtained from an ARMA(1,4) process with parameters \(\phi_1=.3\), \(\theta_1=-.2\), \(\theta_2=-.3\), \(\theta_3=.5\), and \(\theta_4=.2\), while the right plot is from an ARMA(4,1) with parameters \(\phi_1=-.2\), \(\phi_2=-.3\), \(\phi_3=.5\) and \(\phi_4=.2\) and \(\theta_1=.6\). The plots indicate that ARMA models can provide a flexible tool for modeling diverse residual sequences. It will turn out in the next section that all three realizations here come from (strictly) stationary processes. Similar time series plots can be produced in R using the commands
>arima22 =
arima.sim(list(order=c(2,0,2), ar=c(.2,-.3), ma=c(-.5,.3)), n=100)
>arima14 =
arima.sim(list(order=c(1,0,4), ar=.3, ma=c(-.2,-.3,.5,.2)), n=100)
>arima41 =
arima.sim(list(order=c(4,0,1), ar=c(-.2,-.3,.5,.2), ma=.6), n=100)
Some special cases covered in the following two examples have particular relevance in time series analysis.
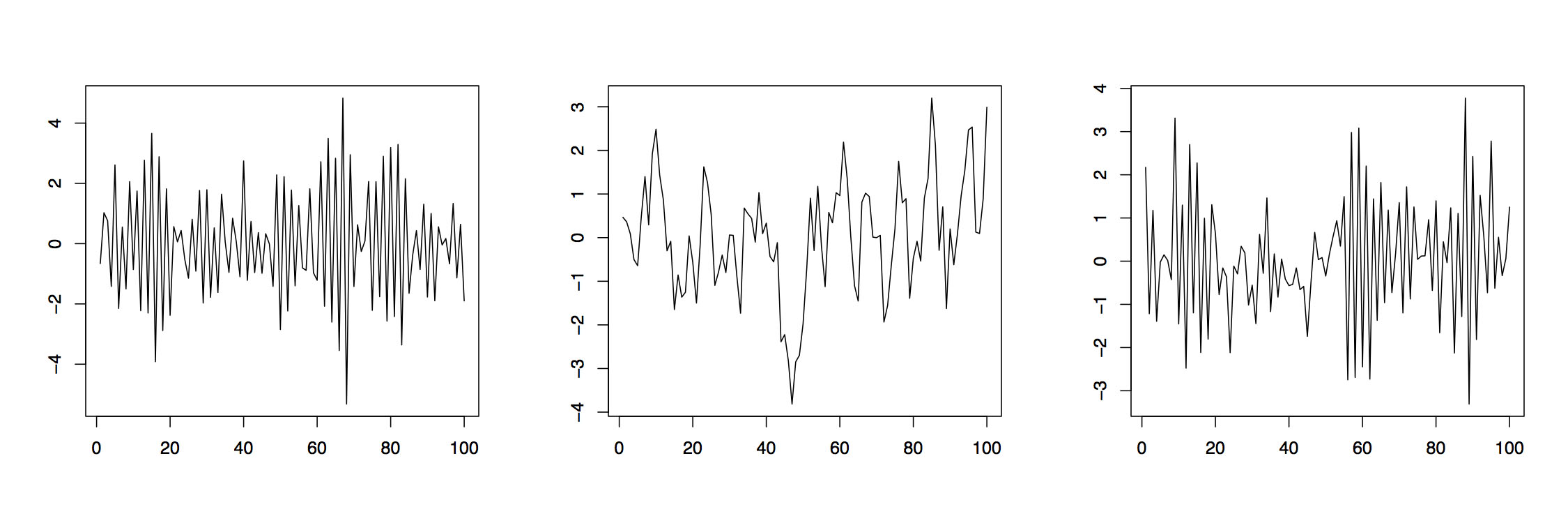
Example 3.1.2 (AR Processes) If the moving average polynomial in (3.1.2) is equal to one, that is, if \(\theta(z)\equiv 1\), then the resulting \((X_t\colon t\in\mathbb{Z})\)is referred to as autoregressive process of order \(p\), AR\((p)\). These time series interpret the value of the current variable \(X_t\) as a linear combination of \(p\) previous variables \(X_{t-1},\ldots,X_{t-p}\) plus an additional distortion by the white noise \(Z_t\). Figure 3.1.2 displays two AR(1) processes with respective parameters \(\phi_1=-.9\) (left) and \(\phi_1=.8\) (middle) as well as an AR(2) process with parameters \(\phi_1=-.5\) and \(\phi_2=.3\). The corresponding R commands are
>ar1neg = arima.sim(list(order=c(1,0,0), ar=-.9), n=100)
>ar1pos = arima.sim(list(order=c(1,0,0), ar=.8), n=100)
>ar2 = arima.sim(list(order=c(2,0,0), ar=c(-.5,.3)), n=100)
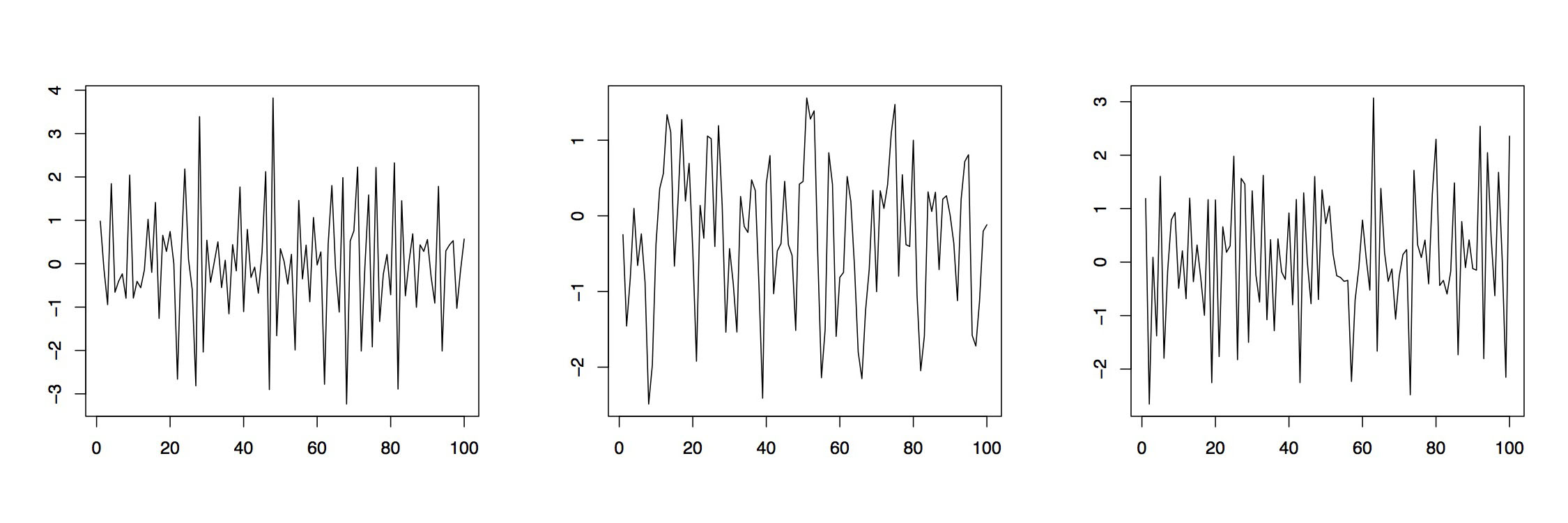
Figure 3.3: Realizations of three moving average processes.
Example 3.1.3 (MA Processes) If the autoregressive polynomial in (3.1.2) is equal to one, that is, if \(\phi(z)\equiv 1\), then the resulting \((X_t\colon t\in\mathbb{Z})\) is referred to as moving average process of order \(q\), MA(\(q\))}. Here the present variable \(X_t\) is obtained as superposition of \(q\) white noise terms \(Z_t,\ldots,Z_{t-q}\). Figure (3.1.3) shows two MA(1) processes with respective parameters \(\theta_1=.5\) (left) and \(\theta_1=-.8\) (middle). The right plot is observed from an MA(2) process with parameters \(\theta_1=-.5\) and \(\theta_2=.3\). In R one may use
> ma1pos = arima.sim(list(order=c(0,0,1), ma=.5), n=100)
> ma1neg = arima.sim(list(order=c(0,0,1), ma=-.8), n=100)
> ma2 = arima.sim(list(order=c(0,0,2), ma=c(-.5,.3)), n=100)
For the analysis upcoming in the next chapters, we now introduce moving average processes of infinite order \((q=\infty)\). They are an important tool for determining stationary solutions to the difference equations (3.1.1).
Definition 3.1.2 Linear processes
A stochastic process \((X_t\colon t\in\mathbb{Z})\) is called linear process or MA\((\infty)\) time series if there is a sequence \((\psi_j\colon j\in\mathbb{N}_0)\) with \(\sum_{j=0}^\infty|\psi_j|<\infty\) such that
\[\begin{equation}\label{eq:3.1.3}
X_t=\sum_{j=0}^\infty\psi_jZ_{t-j},\qquad t\in\mathbb{Z},
\end{equation}\tag{3.1.3} \]
where \((Z_t\colon t\in\mathbb{Z})\sim{\rm WN}(0,\sigma^2)\).
Moving average time series of any order \(q\) are special cases of linear processes. Just pick \(\psi_j=\theta_j\) for \(j=1,\ldots,q\) and set \(\psi_j=0\) if \(j>q\). It is common to introduce the power series
\[ \psi(z)=\sum_{j=0}^\infty\psi_jz^j, \qquad z\in\mathbb{C}, \nonumber \]
to express a linear process in terms of the backshift operator. Display (3.1.3) can now be rewritten in the compact form
\[ X_t=\psi(B)Z_t,\qquad t\in\mathbb{Z}. \nonumber \]
With the definitions of this section at hand, properties of ARMA processes, such as stationarity and invertibility, are investigated in the next section. The current section is closed giving meaning to the notation \(X_t=\psi(B)Z_t\). Note that one is possibly dealing with an infinite sum of random variables. For completeness and later use, in the following example the mean and ACVF of a linear process are derived.
Example 3.1.4 Mean and ACVF of a linear process
Let \((X_t\colon t\in\mathbb{Z})\) be a linear process according to Definition 3.1.2. Then, it holds that
\[ E[X_t] =E\left[\sum_{j=0}^\infty\psi_jZ_{t-j}\right] =\sum_{j=0}^\infty\psi_jE[Z_{t-j}]=0, \qquad t\in\mathbb{Z}. \nonumber \]
Next observe also that
\begin{align*}
\gamma(h)
&=\mathrm{Cov}(X_{t+h},X_t)\\[.2cm]
&=E\left[\sum_{j=0}^\infty\psi_jZ_{t+h-j}\sum_{k=0}^\infty\psi_kZ_{t-k}\right]\\[.2cm]
&=\sigma^2\sum_{k=0}^\infty\psi_{k+h}\psi_k<\infty
\end{align*}
by assumption on the sequence \((\psi_j\colon j\in\mathbb{N}_0)\).


