8.1: Multiple Regressions

It frequently happens that a dependent variable (y) in which we are interested is related to more than one independent variable. If this relationship can be estimated, it may enable us to make more precise predictions of the dependent variable than would be possible by a simple linear regression. Regressions based on more than one independent variable are called multiple regressions.

Multiple linear regression is an extension of simple linear regression and many of the ideas we examined in simple linear regression carry over to the multiple regression setting. For example, scatterplots, correlation, and least squares method are still essential components for a multiple regression.

For example, a habitat suitability index (used to evaluate the impact on wildlife habitat from land use changes) for ruffed grouse might be related to three factors:

x₁ = stem density
x₂ = percent of conifers
x₃ = amount of understory herbaceous matter

A researcher would collect data on these variables and use the sample data to construct a regression equation relating these three variables to the response. The researcher will have questions about his model similar to a simple linear regression model.

• How strong is the relationship between y and the three predictor variables?
• How well does the model fit?
• Have any important assumptions been violated?
• How good are the estimates and predictions?

The general linear regression model takes the form of

\[y_i = \beta_0+ \beta_1x_1+\beta_2x_2 + ...+\beta_kx_k+\epsilon\]

with the mean value of y given as

\[\mu_y = \beta_0 +\beta_1 x_1+\beta_2 x_2+...+\beta_k x_k\]

where:

• y is the random response variable and μy is the mean value of y,
• β0, β1, β2, and βk are the parameters to be estimated based on the sample data,
• x1, x2,…, xk are the predictor variables that are assumed to be non-random or fixed and measured without error, and k is the number of predictor variable,
• and ε is the random error, which allows each response to deviate from the average value of y. The errors are assumed to be independent, have a mean of zero and a common variance (σ2), and are normally distributed.

As you can see, the multiple regression model and assumptions are very similar to those for a simple linear regression model with one predictor variable. Examining residual plots and normal probability plots for the residuals is key to verifying the assumptions.

Correlation

As with simple linear regression, we should always begin with a scatterplot of the response variable versus each predictor variable. Linear correlation coefficients for each pair should also be computed. Instead of computing the correlation of each pair individually, we can create a correlation matrix, which shows the linear correlation between each pair of variables under consideration in a multiple linear regression model.

\(\begin{array}{cccc} & \mathbf{y} & \mathbf{x} 1 & \mathbf{x} 2 \\ \mathbf{x 1} & 0.816 & & \\ & 0.000 & & \\ \mathbf{x 2} & 0.413 & -0.144 & \\ & 0.029 & 0.466 & \\ \mathbf{x 3} & 0.768 & 0.588 & 0.406 \\ & 0.000 & 0.001 & 0.032\end{array}\)

Table \(\PageIndex{1}\) . A correlation matrix.

In this matrix, the upper value is the linear correlation coefficient and the lower value is the p-value for testing the null hypothesis that a correlation coefficient is equal to zero. This matrix allows us to see the strength and direction of the linear relationship between each predictor variable and the response variable, but also the relationship between the predictor variables. For example, y and x1have a strong, positive linear relationship with r = 0.816, which is statistically significant because p = 0.000. We can also see that predictor variables x1 and x3 have a moderately strong positive linear relationship (r = 0.588) that is significant (p = 0.001).

There are many different reasons for selecting which explanatory variables to include in our model (see Model Development and Selection), however, we frequently choose the ones that have a high linear correlation with the response variable, but we must be careful. We do not want to include explanatory variables that are highly correlated among themselves. We need to be aware of any multicollinearity between predictor variables.

Multicollinearity exists between two explanatory variables if they have a strong linear relationship.

For example, if we are trying to predict a person’s blood pressure, one predictor variable would be weight and another predictor variable would be diet. Both predictor variables are highly correlated with blood pressure (as weight increases blood pressure typically increases, and as diet increases blood pressure also increases). But, both predictor variables are also highly correlated with each other. Both of these predictor variables are conveying essentially the same information when it comes to explaining blood pressure. Including both in the model may lead to problems when estimating the coefficients, as multicollinearity increases the standard errors of the coefficients. This means that coefficients for some variables may be found not to be significantly different from zero, whereas without multicollinearity and with lower standard errors, the same coefficients might have been found significant. Ways to test for multicollinearity are not covered in this text, however a general rule of thumb is to be wary of a linear correlation of less than -0.7 and greater than 0.7 between two predictor variables. Always examine the correlation matrix for relationships between predictor variables to avoid multicollinearity issues.

Estimation

Estimation and inference procedures are also very similar to simple linear regression. Just as we used our sample data to estimate β0 and β1 for our simple linear regression model, we are going to extend this process to estimate all the coefficients for our multiple regression models.

With the simpler population model

\[\mu_y = \beta_0+\beta_1x\]

β1 is the slope and tells the user what the change in the response would be as the predictor variable changes. With multiple predictor variables, and therefore multiple parameters to estimate, the coefficients β1, β2, β3 and so on are called partial slopes or partial regression coefficients. The partial slope βi measures the change in y for a one-unit change in xi when all other independent variables are held constant. These regression coefficients must be estimated from the sample data in order to obtain the general form of the estimated multiple regression equation

\[\hat y = b_0+b_1x_1+b_2x_2+b_3x_3+...+b_kx_k\]

and the population model

\[\mu_y = \beta_0 + \beta_1x_1+\beta_2x_2+\beta_3x_3+...+\beta_kx_k\]

where k = the number of independent variables (also called predictor variables)

ŷ = the predicted value of the dependent variable (computed by using the multiple regression equation)

x1, x2, …, xk = the independent variables

β0 is the y-intercept (the value of y when all the predictor variables equal 0)

b0 is the estimate of β0 based on that sample data

β1, β2, β3,…βk are the coefficients of the independent variables x1, x2, …, xk

b1, b2, b3, …, bk are the sample estimates of the coefficients β1, β2, β3,…βk

The method of least-squares is still used to fit the model to the data. Remember that this method minimizes the sum of the squared deviations of the observed and predicted values (SSE).

The analysis of variance table for multiple regression has a similar appearance to that of a simple linear regression.

Source of variation	df	Seq sums of squares	Sums of squares	Mean sums of squares	F
Regression	k		SSR	SSR/k = MSR	MSR/MSE = F
Error	n - k - 1		SSE	SSE/(n - k - 1) = MSE
Total	n -1		SST

Table \(\PageIndex{2}\) . ANOVA table.

Where k is the number of predictor variables and n is the number of observations.

The best estimate of the random variation \(\sigma^2\)—the variation that is unexplained by the predictor variables—is still s2, the MSE. The regression standard error, s, is the square root of the MSE.

A new column in the ANOVA table for multiple linear regression shows a decomposition of SSR, in which the conditional contribution of each predictor variable given the variables already entered into the model is shown for the order of entry that you specify in your regression. These conditional or sequential sums of squares each account for 1 regression degree of freedom, and allow the user to see the contribution of each predictor variable to the total variation explained by the regression model by using the ratio:

\[\dfrac {SeqSS}{SSR}\]

Adjusted \(R^2\)

In simple linear regression, we used the relationship between the explained and total variation as a measure of model fit:

\[R^2 = \dfrac {Explained \ Variation}{Total \ Variation} = \dfrac {SSR}{SSTo} = 1 - \dfrac {SSE}{SSTo}\]

Notice from this definition that the value of the coefficient of determination can never decrease with the addition of more variables into the regression model. Hence, \(R^2\) can be artificially inflated as more variables (significant or not) are included in the model. An alternative measure of strength of the regression model is adjusted for degrees of freedom by using mean squares rather than sums of squares:

\[R^2(adj) = 1 -\dfrac {(n-1)(1-R^2)}{(n-p)} = (1 - \dfrac {MSE}{SSTo/(n-1)})\]

The adjusted \(R^2\) value represents the percentage of variation in the response variable explained by the independent variables, corrected for degrees of freedom. Unlike \(R^2\), the adjusted \(R^2\) will not tend to increase as variables are added and it will tend to stabilize around some upper limit as variables are added.

Tests of Significance

Recall in the previous chapter we tested to see if y and x were linearly related by testing

\(H_0: \beta_1 = 0\)

\(H_1: \beta_1 \ne 0\)

with the t-test (or the equivalent F-test). In multiple linear regression, there are several partial slopes and the t-test and F-test are no longer equivalent. Our question changes: Is the regression equation that uses information provided by the predictor variables x1, x2, x3, …, xk, better than the simple predictor (the mean response value), which does not rely on any of these independent variables?

\(H_0: \beta_1 = \beta_2 = \beta_3 = …=\beta_k = 0\)

\(H1: At \ least \ one \ of β_1, β_2 , β_3 , …β_k \ne 0\)

The F-test statistic is used to answer this question and is found in the ANOVA table.

\[F=\dfrac{MSR}{MSE}\]

This test statistic follows the F-distribution with \(df_1 = k\) and \(df_2 = (n-k-1)\). Since the exact p-value is given in the output, you can use the Decision Rule to answer the question.

If the p-value is less than the level of significance, reject the null hypothesis.

Rejecting the null hypothesis supports the claim that at least one of the predictor variables has a significant linear relationship with the response variable. The next step is to determine which predictor variables add important information for prediction in the presence of other predictors already in the model. To test the significance of the partial regression coefficients, you need to examine each relationship separately using individual t-tests.

\(H_0: β_i = 0\)

\(H_1: β_i \ne 0\)

\[t=\dfrac {b_i-\beta_o}{SE(b_i)} \ with \ df = (n-k-1)\]

where SE(b_i) is the standard error of b_i. Exact p-values are also given for these tests. Examining specific p-values for each predictor variable will allow you to decide which variables are significantly related to the response variable. Typically, any insignificant variables are removed from the model, but remember these tests are done with other variables in the model. A good procedure is to remove the least significant variable and then refit the model with the reduced data set. With each new model, always check the regression standard error (lower is better), the adjusted R² (higher is better), the p-values for all predictor variables, and the residual and normal probability plots.

Because of the complexity of the calculations, we will rely on software to fit the model and give us the regression coefficients. Don’t forget… you always begin with scatterplots. Strong relationships between predictor and response variables make for a good model.

Example \(\PageIndex{1}\):

A researcher collected data in a project to predict the annual growth per acre of upland boreal forests in southern Canada. They hypothesized that cubic foot volume growth (y) is a function of stand basal area per acre (x1), the percentage of that basal area in black spruce (x2), and the stand’s site index for black spruce (x3). α = 0.05.

CuFt	BA/ac	%BA Bspruce	SI		CuFt	BA/ac	%BA Bspruce	SI
55	51	79	45		71	65	93	35
68	100	48	53		67	87	68	41
60	63	67	44		73	108	51	54
40	52	52	31		87	105	82	51
45	67	52	29		80	100	70	45
49	42	82	43		77	103	61	43
62	81	80	42		64	55	96	51
56	70	65	36		60	60	80	47
93	108	96	63		65	70	76	40
76	90	81	60		65	78	74	46
94	110	78	56		83	85	96	55
82	111	59	48		67	92	58	50
86	94	84	53		61	82	58	38
55	82	48	40		51	56	69	35

Table \(\PageIndex{3}\) . Observed data for cubic feet, stand basal area, percent basal area in black spruce, and site index.

Scatterplots of the response variable versus each predictor variable were created along with a correlation matrix.

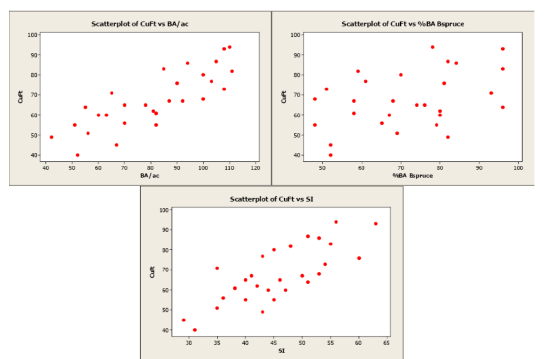
Figure \(\PageIndex{1}\) . Scatterplots of cubic feet versus basal area, percent basal area in black spruce, and site index.

\[ \begin{array}{l}
\text { Correlations: CuFt, BA/ac, %BA Bspruce, SI }\\
\begin{array}{|c|c|c|c|c|}
\hline \mathrm{BA} / \mathrm{ac} & \begin{array}{r}
\text { CuFt } \\
0.816 \\
0.000
\end{array} & \mathrm{BA} / \mathrm{aC} & \frac{8}{8} \mathrm{BA} & \text { Bspruce } \\
\hline \text { ㅇA Bspruce } & \begin{array}{l}
0.413 \\
0.029
\end{array} & \begin{array}{r}
-0.144 \\
0.466
\end{array} & & \\
\hline \text { SI } & \begin{array}{l}
0.768 \\
0.000
\end{array} & \begin{array}{l}
0.588 \\
0.001
\end{array} & & \begin{array}{l}
0.406 \\
0.032
\end{array} \\
\hline
\end{array}
\end{array} \]

Table \(\PageIndex{4}\) . Correlation matrix.

As you can see from the scatterplots and the correlation matrix, BA/ac has the strongest linear relationship with CuFt volume (r = 0.816) and %BA in black spruce has the weakest linear relationship (r = 0.413). Also of note is the moderately strong correlation between the two predictor variables, BA/ac and SI (r = 0.588). All three predictor variables have significant linear relationships with the response variable (volume) so we will begin by using all variables in our multiple linear regression model. The Minitab output is given below.

We begin by testing the following null and alternative hypotheses:

H₀: β₁ = β₂ = β₃ = 0

H₁: At least one of β₁, β₂ , β₃ ≠ 0

General Regression Analysis: CuFt versus BA/ac, SI, %BA Bspruce

Regression Equation: CuFt = -19.3858 + 0.591004 BA/ac + 0.0899883 SI + 0.489441 %BA Bspruce

Coefficients
Term	Coef	SE Coef	T	P	95% CI
Constant	-19.3858	4.15332	-4.6675	0.000	(-27.9578, -10.8137)
BA/ac	0.5910	0.04294	13.7647	0.000	(0.5024, 0.6796)
SI	0.0900	0.11262	0.7991	0.432	(-0.1424, 0.3224)
%BA Bspruce	0.4894	0.05245	9.3311	0.000	(0.3812, 0.5977)
Summary of Model
S = 3.17736		R-Sq = 95.53%		R-Sq(adj) = 94.97%
PRESS = 322.279		R-Sq(pred) = 94.05%
Analysis of Variance
Source	DF	Seq SS	Adj SS	Adj MS	F	P
Regression	3	5176.56	5176.56	1725.52	170.918	0.000000
BA/ac	1	3611.17	1912.79	1912.79	189.467	0.000000
SI	1	686.37	6.45	6.45	0.638	0.432094
%BA Bspruce	1	879.02	879.02	879.02	87.069	0.000000
Error	24	242.30	242.30	10.10
Total	27	5418.86

The F-test statistic (and associated p-value) is used to answer this question and is found in the ANOVA table. For this example, F = 170.918 with a p-value of 0.00000. The p-value is smaller than our level of significance (0.0000<0.05) so we will reject the null hypothesis. At least one of the predictor variables significantly contributes to the prediction of volume.

The coefficients for the three predictor variables are all positive indicating that as they increase cubic foot volume will also increase. For example, if we hold values of SI and %BA Bspruce constant, this equation tells us that as basal area increases by 1 sq. ft., volume will increase an additional 0.591004 cu. ft. The signs of these coefficients are logical, and what we would expect. The adjusted R² is also very high at 94.97%.

The next step is to examine the individual t-tests for each predictor variable. The test statistics and associated p-values are found in the Minitab output and repeated below:

Coefficients
Term	Coef	SE Coef	T	P	95% CI
Constant	-19.3858	4.15332	-4.6675	0.000	(-27.9578, -10.8137)
BA/ac	0.5910	0.04294	13.7647	0.000	( 0.5024, 0.6796)
SI	0.0900	0.11262	0.7991	0.432	( -0.1424, 0.3224)
%BA Bspruce	0.4894	0.05245	9.3311	0.000	( 0.3812, 0.5977)

The predictor variables BA/ac and %BA Bspruce have t-statistics of 13.7647 and 9.3311 and p-values of 0.0000, indicating that both are significantly contributing to the prediction of volume. However, SI has a t-statistic of 0.7991 with a p-value of 0.432. This variable does not significantly contribute to the prediction of cubic foot volume.

This result may surprise you as SI had the second strongest relationship with volume, but don’t forget about the correlation between SI and BA/ac (r = 0.588). The predictor variable BA/ac had the strongest linear relationship with volume, and using the sequential sums of squares, we can see that BA/ac is already accounting for 70% of the variation in cubic foot volume (3611.17/5176.56 = 0.6976). The information from SI may be too similar to the information in BA/ac, and SI only explains about 13% of the variation on volume (686.37/5176.56 = 0.1326) given that BA/ac is already in the model.

The next step is to examine the residual and normal probability plots. A single outlier is evident in the otherwise acceptable plots.

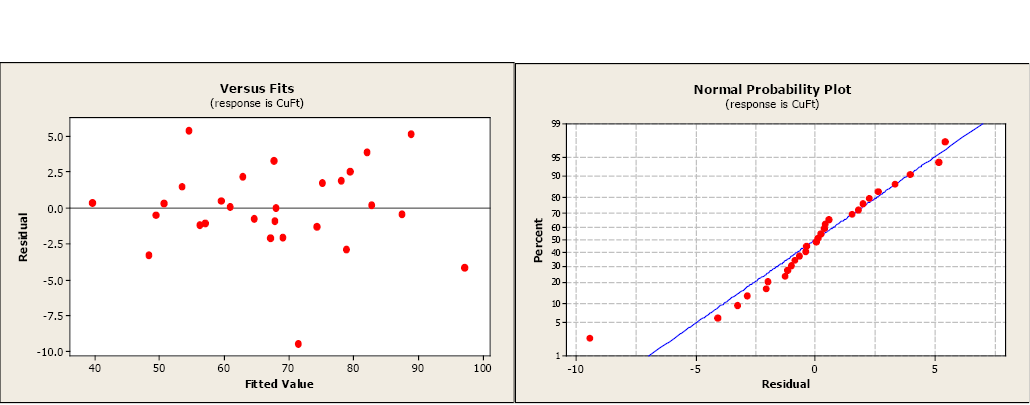
Figure \(\PageIndex{2}\) . Residual and normal probability plots.

So where do we go from here?

We will remove the non-significant variable and re-fit the model excluding the data for SI in our model. The Minitab output is given below.

General Regression Analysis: CuFt versus BA/ac, %BA Bspruce

Regression Equation
CuFt = -19.1142 + 0.615531 BA/ac + 0.515122 %BA Bspruce
Coefficients
Term	Coef	SE Coef	T	P	95% CI
Constant	-19.1142	4.10936	-4.6514	0.000	(-27.5776, -10.6508)
BA/ac	0.6155	0.02980	20.6523	0.000	(0.5541, 0.6769)
%BA Bspruce	0.5151	0.04115	12.5173	0.000	(0.4304, 0.5999)
Summary of Model
S = 3.15431		R-Sq = 95.41%		R-Sq(adj) = 95.04%
PRESS = 298.712		R-Sq(pred) = 94.49%
Analysis of Variance
Source	DF	SeqSS	AdjSS	AdjMS	F	P
Regression	2	5170.12	5170.12	2585.06	259.814	0.0000000
BA/ac	1	3611.17	4243.71	4243.71	426.519	0.0000000
%BA Bspruce	1	1558.95	1558.95	1558.95	156.684	0.0000000
Error	25	248.74	248.74	9.95
Total	27	5418.86

We will repeat the steps followed with our first model. We begin by again testing the following hypotheses:

\(H_0: \beta_1 = \beta_2 = \beta_3 = 0\)

\(H_1: At \ least \ one \ of \ \beta_1, \beta_2 , \beta_3 \ne 0\)

This reduced model has an F-statistic equal to 259.814 and a p-value of 0.0000. We will reject the null hypothesis. At least one of the predictor variables significantly contributes to the prediction of volume. The coefficients are still positive (as we expected) but the values have changed to account for the different model.

The individual t-tests for each coefficient (repeated below) show that both predictor variables are significantly different from zero and contribute to the prediction of volume.

Coefficients
Term	Coef	SE Coef	T	P	95% CI
Constant	-19.1142	4.10936	-4.6514	0.000	(-27.5776, -10.6508)
BA/ac	0.6155	0.02980	20.6523	0.000	( 0.5541, 0.6769)
%BA Bspruce	0.5151	0.04115	12.5173	0.000	( 0.4304, 0.5999)

Notice that the adjusted R2 has increased from 94.97% to 95.04% indicating a slightly better fit to the data. The regression standard error has also changed for the better, decreasing from 3.17736 to 3.15431 indicating slightly less variation of the observed data to the model.

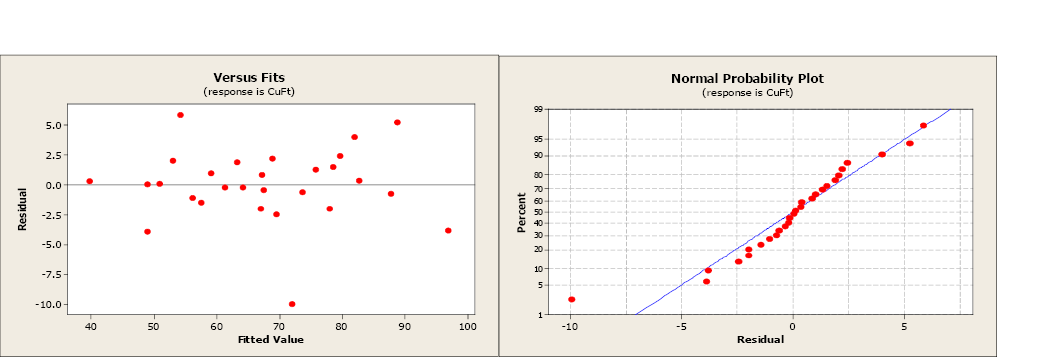
Figure \(\PageIndex{3}\) . Residual and normal probability plots.

The residual and normal probability plots have changed little, still not indicating any issues with the regression assumption. By removing the non-significant variable, the model has improved.