6.9: Chi-square distribution

As noted earlier, the normal deviate or Z score can be viewed as randomly sampled from the standard normal distribution. The chi-square distribution describes the probability distribution of the squared standardized normal deviates with degrees of freedom, \(df\), equal to the number of samples taken. (The number of independent pieces of information needed to calculate the estimate, see Ch. 8.) We will use the chi-square distribution to test statistical significance of categorical variables in goodness of fit tests and contingency table problems.

The equation of the chi-square is \[\chi^{2} = \sum_{i=1}^{k} \frac{\left(f_{i} - \hat{f}_{i}\right)^{2}}{\hat{f}_{i}} \nonumber\]

where \(k\) is the number of groups or categories, from 1 to \(k\), and \(f_{i}\) is the observed frequency and \(\hat{f}_{i}\) is the expected frequency for the \(k^{th}\) category. We call the result of this calculation the chi-square test statistic. We evaluate how often that value or greater of a test statistic will occur by applying the chi-square distribution function. Graphs to show chi-square distribution for degrees of freedom equal to 1 through 5, 10, and 20 (Fig. \(\PageIndex{1}\)).

Figure \(\PageIndex{1}\): Animated GIF of plots of chi-square distribution over a range of degrees of freedom.

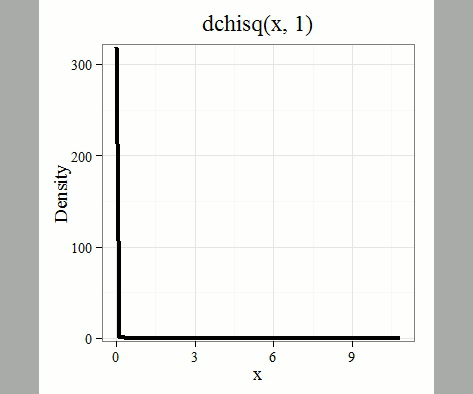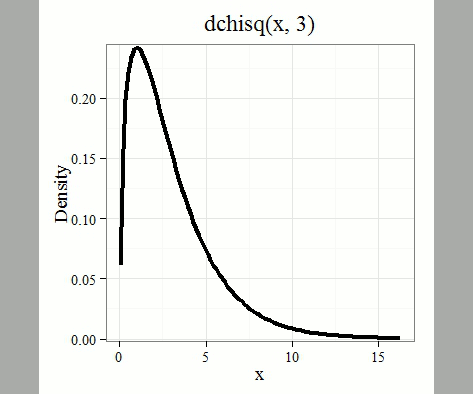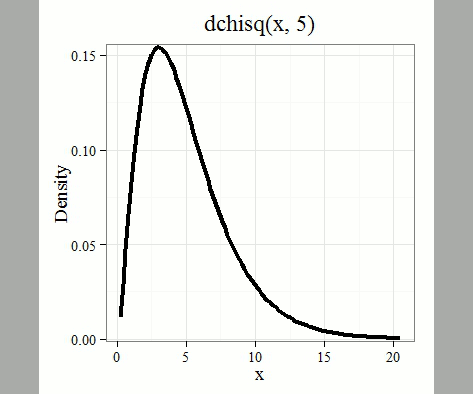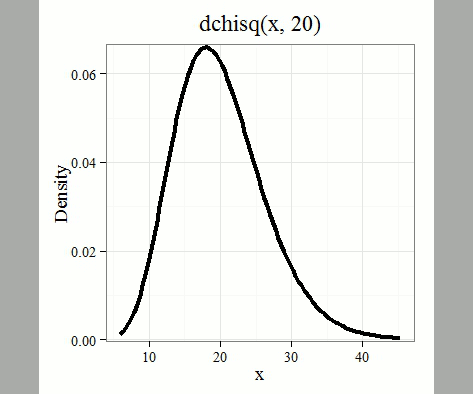
Note that the distribution is asymmetric, particularly at low degrees of freedom. Thus, tests using the chi-square are one-tailed (Fig. \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): The test of the chi-square is typically one-tailed. In this case, the highlighted area shows the probability of values greater than the critical value.

By convention in the Null Hypothesis Significance Testing protocol (NHST), we compare the test statistic to a critical value. The critical value is defined as the value of the test statistic — the cutoff boundary between statistical significance and insignificance — that occurs at the Type I error rate, which is typically set to 5%. The interpretation of the result is as follows: after calculating a test statistic, we can judge significance of the results relative to the null hypothesis expectation. If our test statistics is greater than the critical value, then the p-value of our results are less than 5% (R will report an exact p-value for the test statistic). You are not expected to be able to follow this logic just yet — rather, we teach it now as a sort of mechanical understanding to develop in the NHST tradition. The justification for this approach to testing of statistical significance is developed in Chapter 8. A portion of the critical values of the chi-square distribution are shown in Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\): Portion of the table of some critical values of chi-square distribution, one tailed (right-tailed or “upper” portion of distribution).

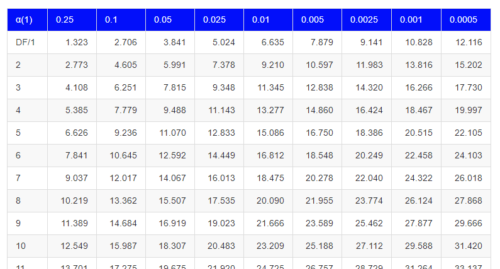
See Appendix for a complete chi-square table.

Example

Professor Hermon Bumpus of Brown University in Providence, Rhode Island, received 136 House Sparrows (Passer domesticus) after a severe winter storm 1 February 1898. The birds were collected from the ground; 72 of the birds survived, 64 did not (Table \(\PageIndex{1}\)). Bumpus made several measures of morphology on the birds and the data set has served as a classical example of Natural Selection (Chicago Field Museum). We’ll look at this data set when we introduce Linear Regression.

Table \(\PageIndex{1}\). Survival statistics of Bumpus House sparrows.

	Yes	No
Female	21	28
Male	51	36

Was there a survival difference between male and female House Sparrows? This is a classic contingency table analysis, something we will at length in Chapter 9. For now, we report the Chi-square test statistic for this test was 3.1264 and the test had one degree of freedom. What is the critical value of the chi-square distribution at 5% and one degree of freedom?. Typically we would simply use R to look this up

qchisq(c(0.05), df=1, lower.tail=FALSE)

But we can also get this from the table of critical values (Fig. \(\PageIndex{4}\)). Simply select the row based on the degrees of freedom for the test then scan to the column with the appropriate significance level, again, typically 5% (0.05).

Figure \(\PageIndex{4}\): Portion of the chi-square distribution which shows how to find critical value of the chi-square distribution.

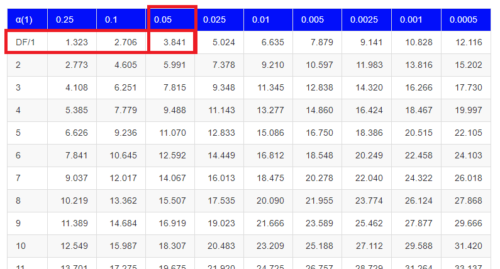
For 1 degree of freedom at 5% significance, the critical value is 3.841. Back to our hypothesis: Did male and female survival differ in the Bumpus data set? Following the NHST logic, if the test statistic value (e.g., 3.1264) is greater than the critical value (3.841), then we would reject the null hypothesis. For this example, we would conclude no statistical difference between male and female survival because the test statistic was smaller than the critical value. How likely are these results due to chance? That’s where the p-value comes in. Our test statistic value falls between 5% and 10% (2.706 < 3.1264 < 3.841). In order to get the actual p-value of our test statistic we would need to use R.

R code

Given a chi-square test statistic, you can use R to calculate the probability of that value against the null hypothesis. At the R prompt, enter:

pchisq(c(3.1264), df=1, lower.tail=FALSE)

The R output is

[1] 0.07703368

Because we are using R Commander, simply select the command by following the menu options.

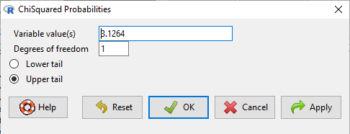
Rcmdr: Distributions → Continuous distributions → Chi-squared distribution → Chi-squared probabilities …

Enter the chi-square value and degrees of freedom (Fig. \(\PageIndex{5}\)).

Figure \(\PageIndex{5}\): Screenshot of input box in Rcmdr for Chi-square probability values.

---

Questions

1. What happens to the shape of the chi-square distribution as degrees of freedom are increased from 1 to 5 to 20 to 100?

Be able to answer the following questions using the Chi-square table or using Rcmdr:

2. For probability \(\alpha = 5\%\), what is the critical value of the chi-square distribution (upper tail)?
3. The value of the chi-square test statistic is given as 12. With 3 degrees of freedom, what is the approximate probability of this value or greater from the chi-square distribution?