20.9: Survival analysis
- Page ID
- 45286
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)[Page rough draft]
Introduction
As the name suggests, survival analysis is a branch of statistics used to account for death of organisms, or more generally, failure in a system. In general, this kind of analysis models time to event, where event would be death or failure. The basics of the method is defined by the survival function
\[S_{t} = Pr (T < t) \nonumber\]
where \(t\) is time, \(T\) is a variable that represents time of death or other end point, and \(Pr\) is probability of an event occurring later than at time \(t\).
Excellent resources available, series of articles in volume 89 of British Journal of Cancer: Clark et al (2003a), Bradburn et al (2003a), Bradburn et al (2003b), and Clark et al (2003b).
Hazard function
Defined as the event rate at time \(t\) based on survival for time times equal to or greater than \(t\).
Censoring
Censoring is a a missing data problem typical of survival analysis. Distinguish right-censored and left-censored.
Kaplan-Meier plot
Kaplan-Meier (KM) estimator of survival function. Other survival function estimators Fleming-Harrington. The KM estimator, \(\hat{S}_{t}\) is \[\hat{S}(t) = \prod_{i: t_{i} \leq t} \left(1 - \frac{d_{i}}{n_{i}}\right) \nonumber\]
where \(d_{i}\) is the number of events that occurred at time \(t_{i}\), \(n_{i}\) is the number of individuals known to have survived or not been censored. Because it’s an estimate, a statistic, we need an estimate of the error variance. Several options, the default in R is the Greenwood estimator. \[var \left(\hat{S}(t)\right) = \hat{S}(t)^{2} \sum_{i: t_{i} \leq t} \frac{d_{i}}{n_{i} \left(n_{i} - d_{i}\right)} \nonumber\]
The KM plot, censoring times noted with plus.
R code
Download and install the RcmdrPlugin.survival package.
Example
data(heart, package="survival")
attach(heart)
#Get help with the data set
help("heart", package="survival")
head(heart)
start stop event age year surgery transplant id 1 0 50 1 -17.155373 0.1232033 0 0 1 2 0 6 1 3.835729 0.2546201 0 0 2 3 0 1 0 6.297057 0.2655715 0 0 3 4 1 16 1 6.297057 0.2655715 0 1 3 5 0 36 0 -7.737166 0.4900753 0 0 4 6 36 39 1 -7.737166 0.4900753 0 1 4
Run basic survival analysis. After installing the RcmdrPlugin.survival, from Rcmdr select estimate survival function.
Get survival estimator and KM plot (Figure \(\PageIndex{2}\))
R output:
.Survfit <- survfit(Surv(start, event) ~ 1, conf.type="log", conf.int=0.95, Rcmdr+ type="kaplan-meier", error="greenwood", data=heart) .Survfit Call: survfit(formula = Surv(start, event) ~ 1, data = heart, error = "greenwood", conf.type = "log", conf.int = 0.95, type = "kaplan-meier") n events median 0.95LCL 0.95UCL 172 75 26 17 37 plot(.Survfit, mark.time=TRUE) quantile(.Survfit, quantiles=c(.25,.5,.75)) $quantile 25 50 75 3 26 67 $lower 25 50 75 1 17 46 $upper 25 50 75 12 37 NA #by default, Rcmdr removes the object remove(.Survfit)

I modified the plot() code with these additions
ylim = c(0,1), ylab="Survival probability", xlab="Days", lwd=2, col="blue"
the data set includes age and whether or not subjects had heart surgery before transplant. Compare.
Variable surgery is recorded 0,1, so need to create a factor
fSurgery <- as.factor(surgery)
Now, to compare
Rcmdr: Statistics → Survival analysis → Compare survival functions…
R output
Rcmdr> survdiff(Surv(start,event) ~ fSurgery, rho=0, data=heart)
Call:
survdiff(formula = Surv(start, event) ~ fSurgery, data = heart,
rho = 0)
N Observed Expected (O-E)^2/E (O-E)^2/V
fSurgery=No 143 66 58.7 0.902 4.56
fSurgery=Yes 29 9 16.3 3.255 4.56
Chisq= 4.6 on 1 degrees of freedom, p= 0.03
Get the KM estimator and make a KM plot
mySurvfit <- survfit(Surv(start, event) ~ surgery, conf.type="log", conf.int=0.95,
type="kaplan-meier", error="greenwood", data=heart)
plot(mySurvfit, mark.time=TRUE, ylim=c(0,1),lwd=2, col=c("blue","red"), xlab="Number of days", ylab="Survival probability")
legend("topright", legend = paste(c("Surgery - No", "Surgery - Yes")), col = c("blue", "red"), pch = 19, bty = "n")

The comparison plot can be made in Rcmdr by selecting our Surgery factor in Strata setting (Fig. \(\PageIndex{4}\)). Recall that strata refers to subgroups of a population.
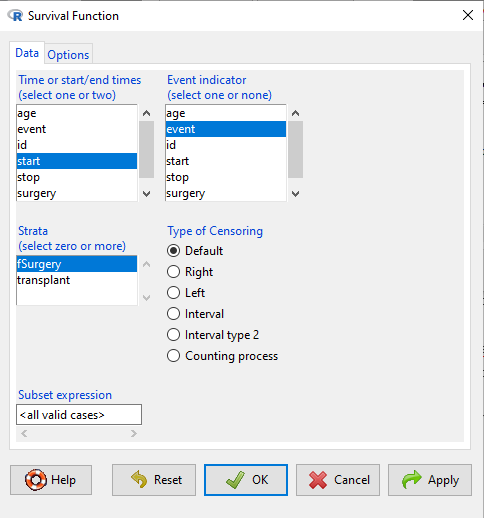
Questions
[pending]


