18.2: Nonlinear regression
- Page ID
- 45259
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
The linear model is incredibly relevant in so many cases. A quick look for “linear model” in PUBMED returns about 22 thousand hits; 3.7 million in Google Scholar; 3 thousand hits in ERIC database. These results compare to search of “statistics” in the same databases: 2.7 million (PUBMED), 7.8 million (Google Scholar), 61.4 thousand (ERIC). But all models are not the same.
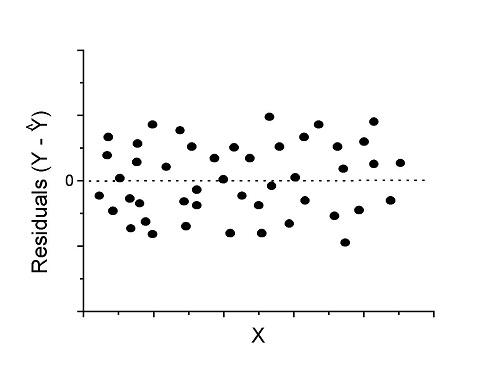
Fit of a model to the data can be evaluated by looking at the plots of residuals (Fig. \(\PageIndex{1}\)), where we expect to find random distribution of residuals across the range of predictor variable.
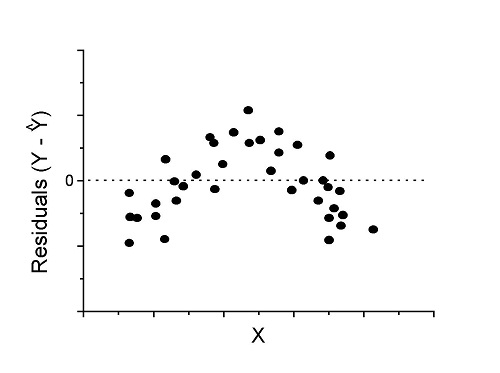
However, clearly, there are problems for which assumption of fit to line is not appropriate. We see this, again, in patterns of residuals, e.g., Figure \(\PageIndex{2}\).
Fitting of polynomial linear model
Fit simple linear regression, using data linked at end of page. Data sourced from Yuan et al. (2012), https://phenome.jax.org/projects/Yuan2.
R code:
LinearModel.1 <- lm(cumFreq~Months, data=yuan)
summary(LinearModel.1)
Call:
lm(formula = cumFreq ~ Months, data = yuan)
Residuals:
Min 1Q Median 3Q Max
-0.11070 -0.07799 -0.01728 0.06982 0.13345
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.132709 0.045757 -2.90 0.0124 *
Months 0.029605 0.001854 15.97 6.37e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.09308 on 13 degrees of freedom
Multiple R-squared: 0.9515, Adjusted R-squared: 0.9477
F-statistic: 254.9 on 1 and 13 DF, p-value: 6.374e-10
We see from the \(R^{2}\) (95%), a high degree of fit to the data. However, residual plot reveals obvious trend (Fig. \(\PageIndex{3}\))
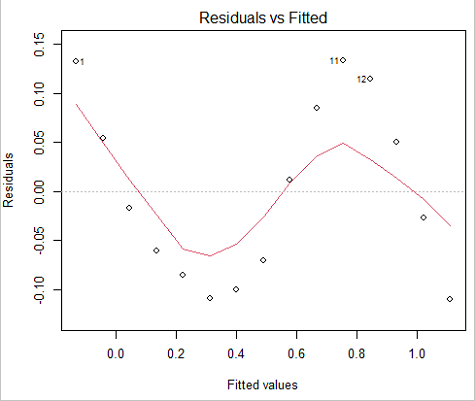
We can fit a polynomial regression.
First, a second order polynomial:
LinearModel.2 <- lm(cumFreq ~ poly( Months, degree=2), data=yuan)
summary(LinearModel.2)
Call:
lm(formula = cumFreq ~ poly(Months, degree = 2), data = yuan)
Residuals:
Min 1Q Median 3Q Max
-0.13996 -0.06720 -0.02338 0.07153 0.14277
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.48900 0.02458 19.891 1.49e-10 ***
poly(Months, degree = 2)1 1.48616 0.09521 15.609 2.46e-09 ***
poly(Months, degree = 2)2 0.06195 0.09521 0.651 0.528
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.09521 on 12 degrees of freedom
Multiple R-squared: 0.9531, Adjusted R-squared: 0.9453
F-statistic: 122 on 2 and 12 DF, p-value: 0.0000000106
Second, try a third order polynomial:
LinearModel.3 <- lm(cumFreq ~ poly(Months, degree = 3), data=yuan)
summary(LinearModel.3)
Call:
lm(formula = cumFreq ~ poly(Months, degree = 3), data = yuan)
Residuals:
Min 1Q Median 3Q Max
-0.052595 -0.021533 0.001023 0.025166 0.048270
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.488995 0.008982 54.442 9.90e-15 ***
poly(Months, degree = 3)1 1.486157 0.034787 42.722 1.41e-13 ***
poly(Months, degree = 3)2 0.061955 0.034787 1.781 0.103
poly(Months, degree = 3)3 -0.308996 0.034787 -8.883 2.38e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.03479 on 11 degrees of freedom
Multiple R-squared: 0.9943, Adjusted R-squared: 0.9927
F-statistic: 635.7 on 3 and 11 DF, p-value: 1.322e-12
Which model is best? We are tempted to compare R-squared among the models, but R2 turn out to be untrustworthy here. Instead, we compare using the Akaike Information Criterion, AIC
R code/results:
AIC(LinearModel.1,LinearModel.2, LinearModel.3)
df AIC
LinearModel.1 3 -24.80759
LinearModel.2 4 -23.32771
LinearModel.3 5 -52.83981
Smaller the AIC, better fit.
anova(RegModel.5,LinearModel.3, LinearModel.4) Analysis of Variance Table Model 1: cumFreq ~ Months Model 2: cumFreq ~ poly(Months, degree = 2) Model 3: cumFreq ~ poly(Months, degree = 3) Res.Df RSS Df Sum of Sq F Pr(>F) 1 13 0.112628 2 12 0.108789 1 0.003838 3.1719 0.1025 3 11 0.013311 1 0.095478 78.9004 0.000002383 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Logistic regression
The Logistic regression is a classic example of nonlinear model.
R code
logisticModel <-nls(cumFreq~DD/(1+exp(-(CC+bb*Months))), start=list(DD=1,CC=0.2,bb=.5),data=yuan,trace=TRUE) 5.163059 : 1.0 0.2 0.5 2.293604 : 0.90564552 -0.07274945 0.11721201 1.109135 : 0.96341283 -0.60471162 0.05066694 0.429202 : 1.29060000 -2.09743525 0.06785993 0.3863037 : 1.10392723 -2.14457296 0.08133307 0.2848133 : 0.9785669 -2.4341333 0.1058674 0.1080423 : 0.9646295 -3.1918526 0.1462331 0.005888491 : 1.0297915 -4.3908114 0.1982491 0.004374918 : 1.0386521 -4.6096564 0.2062024 0.004370212 : 1.0384803 -4.6264657 0.2068853 0.004370201 : 1.0385065 -4.6269276 0.2068962 0.004370201 : 1.0385041 -4.6269822 0.2068989
summary(logisticModel)
Formula: yuan$cumFreq ~ DD/(1 + exp(-(CC + bb * yuan$Months)))
Parameters:
Estimate Std. Error t value Pr(>|t|)
DD 1.038504 0.014471 71.77 < 2e-16 ***
CC -4.626982 0.175109 -26.42 5.29e-12 ***
bb 0.206899 0.008777 23.57 2.03e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.01908 on 12 degrees of freedom
Number of iterations to convergence: 11
Achieved convergence tolerance: 0.000006909
> AIC(logisticModel)
[1] -71.5467
Logistic regression is a statistical method for modeling the dependence of a categorical (binomial) outcome variable on one or more categorical and continuous predictor variables (Bewick et al 2005).
The logistic function is used to transform a sigmoidal curve to a more or less straight line while also changing the range of the data from binary (0 to 1) to infinity \((-\infty, +\infty)\). For event with probability of occurring \(p\), the logistic function is written as \[logit(p) = \ln \left(\frac{p}{1-p}\right) \nonumber\]
where \(\ln\) refers to the natural logarithm.
This is an odds ratio. It represents the effect of the predictor variable on the chance that the event will occur.
The logistic regression model then very much resembles the same as we have seen before. \[logit(p) = \beta_{0} + \beta_{1} X_{1} + \beta_{2} X_{2} + \ldots + \beta_{n} X_{n} + \epsilon \nonumber\]
In R and Rcmdr we use the glm() function to model the logistic function. Logistic regression is used to model a binary outcome variable. What is a binary outcome variable? It is categorical! Examples include: Living or Dead; Diabetes Yes or No; Coronary artery disease Yes or No. Male or Female. One of the categories could be scored 0, the other scored 1. For example, living might be 0 and dead might be scored as 1. (By the way, for a binomial variable, the mean for the variable is simply the number of experimental units with “1” divided by the total sample size.)
With the addition of a binary response variable, we are now really close to the Generalized Linear Model. Now we can handle statistical models in which our predictor variables are either categorical or ratio scale. All of the rules of crossed, balanced, nested, blocked designs still apply because our model is still of a linear form.
We write our generalized linear model \[G \sim Model \nonumber\]
just to distinguish it from a general linear model with the ratio-scale \(Y\) as the response variable.
Think of the logistic regression as modeling a threshold of change between the 0 and the 1 value. In another way, think of all of the processes in nature in which there is a slow increase, followed by a rapid increase once a transition point is met, only to see the rate of change slow down again. Growth is like that. We start small, stay relatively small until birth, then as we reach our early teen years, a rapid change in growth (height, weight) is typically seen (well, not in my case … at least for the height). The fitted curve I described is a logistic one (other models exist too). Where the linear regression function was used to minimize the squared residuals as the definition of the best fitting line, now we use the logistic as one possible way to describe or best fit this type of a curved relationship between an outcome and one or more predictor variables. We then set out to describe a model which captures when an event is unlikely to occur (the probability of dying is close to zero) AND to also describe when the event is highly likely to occur (the probability is close to one).
A simple way to view this is to think of time being the predictor \((X)\) variable and risk of dying. If we’re talking about the lifetime of a mouse (lifespan typically about 18-36 months), then the risk of dying at one month is very low, and remains low through adulthood until the mouse begins the aging process. Here’s what the plot might look like, with the probability of dying at age \(X\) on the \(Y\) axis (probability = 0 to 1) (Fig. \(\PageIndex{4}\)).
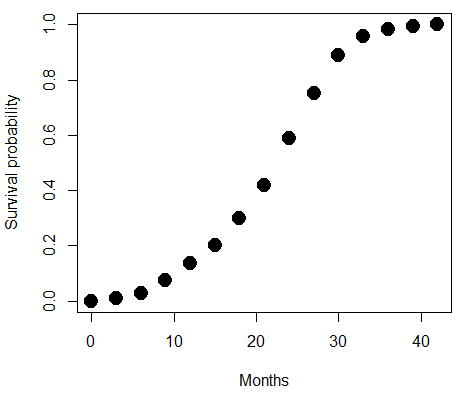
We ask — of all the possible models we could draw, which best fits the data? The curve fitting process is called the logistic regression.
With some minor, but important differences, running the logistic regression is the same as what you have been doing so far for ANOVA and for linear regression. In Rcmdr, access the logistic regression function by invoking the Generalized Linear Model (Fig. 5).
Rcmdr: Statistics → Fit models → Generalized linear model.

Select the model as before. The box to the left accepts your binomial dependent variable; the box at right accepts your factors, your interactions, and your covariates. It permits you to inform R how to handle the factors: Crossed? Just enter the factors and follow each with a plus. If fully crossed, then the interactions may be specified with “:” to explicitly call for a two-way interaction between two (A:B) or a three-way interaction between three (A:B:C) variables. In the later case, if all of the two way interactions are of interest, simply typing A*B*C would have done it. If nested, then use %in% to specify the nesting factor.
R output:
> GLM.1 <- glm(cumFreq ~ Months, family=gaussian(identity), data=yuan) > summary(GLM.1) Call: glm(formula = cumFreq ~ Months, family = gaussian(identity), data = yuan) Deviance Residuals: Min 1Q Median 3Q Max -0.11070 -0.07799 -0.01728 0.06982 0.13345 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.132709 0.045757 -2.90 0.0124 * Months 0.029605 0.001854 15.97 6.37e-10 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for gaussian family taken to be 0.008663679) Null deviance: 2.32129 on 14 degrees of freedom Residual deviance: 0.11263 on 13 degrees of freedom AIC: -24.808 Number of Fisher Scoring iterations: 2
Assessing fit of the logistic regression model
Some of the differences you will see with the logistic regression is the term deviance. Deviance in statistics simply means compare one model to another and calculate some test statistic we’ll call “the deviance.” We then evaluate the size of the deviance like a chi-square goodness of fit. If the model fits the data poorly (residuals large relative to the predicted curve), then the deviance will be small and the probability will also be high — the model explains little of the data variation. On the other hand, if the deviance is large, then the probability will be small — the model explains the data, and the probability associated with the deviance will be small (significantly so? You guessed it! \(P < 0.05\)).
The Wald test statistic is \[\left(\frac{\beta_{n}}{SE_{\beta_{n}}}\right)^{2} \nonumber\]
where \(n\) and \(\beta\) refer to any of the \(n\) coefficients from the logistic regression equation and \(SE\) refers to the standard error if the coefficient. The Wald test is used to test the statistical significance of the coefficients. It is distributed approximately as a chi-squared probability distribution with one degree of freedom. The Wald test is reasonable, but has been found to give values that are not possible for the parameter (e.g., negative probability).
Likelihood ratio tests are generally preferred over the Wald test. For a coefficient, the likelihood test is written as \[-2 \times \ln (likelihood \ ratio) = -2 \ln \left( L_{0}/L_{1} \right) = -2 \times \left(\ln L_{0} - \ln L_{1}\right) \nonumber\]
where \(L_{0}\) is the likelihood of the data when the coefficient is removed from the model (i.e., set to zero value), whereas \(L_{1}\) is the likelihood of the data when the coefficient is the estimated value of the coefficient. It is also distributed approximately as a chi-squared probability distribution with one degree of freedom.
Questions
[pending]
Data set
| Months | freq | cumFreq |
| 0 | 0 | 0 |
| 3 | 0.01063264221159 | 0.01063264221159 |
| 6 | 0.017012227538543 | 0.027644869750133 |
| 9 | 0.045188729399256 | 0.072833599149389 |
| 12 | 0.064327485380117 | 0.137161084529506 |
| 15 | 0.064859117490697 | 0.202020202020202 |
| 18 | 0.097820308346624 | 0.299840510366826 |
| 21 | 0.118553960659224 | 0.41839447102605 |
| 24 | 0.171185539606592 | 0.589580010632642 |
| 27 | 0.162147793726741 | 0.751727804359383 |
| 30 | 0.137161084529506 | 0.888888888888889 |
| 33 | 0.069643806485912 | 0.958532695374801 |
| 36 | 0.024455077086656 | 0.982987772461457 |
| 39 | 0.011695906432749 | 0.994683678894205 |
| 42 | 0.005316321105795 | 1 |


