16.1: Factorial ANOVA 1- Balanced Designs, No Interactions
- Page ID
- 4042
When we discussed analysis of variance in Chapter 14, we assumed a fairly simple experimental design: each person falls into one of several groups, and we want to know whether these groups have different means on some outcome variable. In this section, I’ll discuss a broader class of experimental designs, known as factorial designs, in we have more than one grouping variable. I gave one example of how this kind of design might arise above. Another example appears in Chapter 14, in which we were looking at the effect of different drugs on the mood.gain experienced by each person. In that chapter we did find a significant effect of drug, but at the end of the chapter we also ran an analysis to see if there was an effect of therapy. We didn’t find one, but there’s something a bit worrying about trying to run two separate analyses trying to predict the same outcome. Maybe there actually is an effect of therapy on mood gain, but we couldn’t find it because it was being “hidden” by the effect of drug? In other words, we’re going to want to run a single analysis that includes both drug and therapy as predictors. For this analysis each person is cross-classified by the drug they were given (a factor with 3 levels) and what therapy they received (a factor with 2 levels). We refer to this as a 3×2 factorial design. If we cross-tabulate drug by therapy, using the xtabs() function (see Section 7.1), we get the following table:230
load("./rbook-master/data/clinicaltrial.rdata")
xtabs( ~ drug + therapy, clin.trial )## therapy
## drug no.therapy CBT
## placebo 3 3
## anxifree 3 3
## joyzepam 3 3As you can see, not only do we have participants corresponding to all possible combinations of the two factors, indicating that our design is completely crossed, it turns out that there are an equal number of people in each group. In other words, we have a balanced design. In this section I’ll talk about how to analyse data from balanced designs, since this is the simplest case. The story for unbalanced designs is quite tedious, so we’ll put it to one side for the moment.
What hypotheses are we testing?
Like one-way ANOVA, factorial ANOVA is a tool for testing certain types of hypotheses about population means. So a sensible place to start would be to be explicit about what our hypotheses actually are. However, before we can even get to that point, it’s really useful to have some clean and simple notation to describe the population means. Because of the fact that observations are cross-classified in terms of two different factors, there are quite a lot of different means that one might be interested. To see this, let’s start by thinking about all the different sample means that we can calculate for this kind of design. Firstly, there’s the obvious idea that we might be interested in this table of group means:
aggregate( mood.gain ~ drug + therapy, clin.trial, mean )## drug therapy mood.gain
## 1 placebo no.therapy 0.300000
## 2 anxifree no.therapy 0.400000
## 3 joyzepam no.therapy 1.466667
## 4 placebo CBT 0.600000
## 5 anxifree CBT 1.033333
## 6 joyzepam CBT 1.500000Now, this output shows a cross-tabulation of the group means for all possible combinations of the two factors (e.g., people who received the placebo and no therapy, people who received the placebo while getting CBT, etc). However, we can also construct tables that ignore one of the two factors. That gives us output that looks like this:
aggregate( mood.gain ~ drug, clin.trial, mean )## drug mood.gain
## 1 placebo 0.4500000
## 2 anxifree 0.7166667
## 3 joyzepam 1.4833333 aggregate( mood.gain ~ therapy, clin.trial, mean )## therapy mood.gain
## 1 no.therapy 0.7222222
## 2 CBT 1.0444444But of course, if we can ignore one factor we can certainly ignore both. That is, we might also be interested in calculating the average mood gain across all 18 participants, regardless of what drug or psychological therapy they were given:
mean( clin.trial$mood.gain )## [1] 0.8833333At this point we have 12 different sample means to keep track of! It is helpful to organise all these numbers into a single table, which would look like this:
knitr::kable(tibble::tribble(
~V1, ~V2, ~V3, ~V4,
NA, "no therapy", "CBT", "total",
"placebo", "0.30", "0.60", "0.45",
"anxifree", "0.40", "1.03", "0.72",
"joyzepam", "1.47", "1.50", "1.48",
"total", "0.72", "1.04", "0.88"
), col.names = c("", "no therapy", "CBT", "total"))| no therapy | CBT | total | |
|---|---|---|---|
| NA | no therapy | CBT | total |
| placebo | 0.30 | 0.60 | 0.45 |
| anxifree | 0.40 | 1.03 | 0.72 |
| joyzepam | 1.47 | 1.50 | 1.48 |
| total | 0.72 | 1.04 | 0.88 |
Now, each of these different means is of course a sample statistic: it’s a quantity that pertains to the specific observations that we’ve made during our study. What we want to make inferences about are the corresponding population parameters: that is, the true means as they exist within some broader population. Those population means can also be organised into a similar table, but we’ll need a little mathematical notation to do so. As usual, I’ll use the symbol μ to denote a population mean. However, because there are lots of different means, I’ll need to use subscripts to distinguish between them.
Here’s how the notation works. Our table is defined in terms of two factors: each row corresponds to a different level of Factor A (in this case drug), and each column corresponds to a different level of Factor B (in this case therapy). If we let R denote the number of rows in the table, and C denote the number of columns, we can refer to this as an R×C factorial ANOVA. In this case R=3 and C=2. We’ll use lowercase letters to refer to specific rows and columns, so μrc refers to the population mean associated with the rth level of Factor A (i.e. row number r) and the cth level of Factor B (column number c).231 So the population means are now written like this:
knitr::kable(tibble::tribble(
~V1, ~V2, ~V3, ~V4,
"placebo", "$\\mu_{11}$", "$\\mu_{12}$", "",
"anxifree", "$\\mu_{21}$", "$\\mu_{22}$", "",
"joyzepam", "$\\mu_{31}$", "$\\mu_{32}$", "",
"total", "", "", ""
), col.names = c( "", "no therapy", "CBT", "total"))| no therapy | CBT | total | |
|---|---|---|---|
| placebo | μ11 | μ12 | |
| anxifree | μ21 | μ22 | |
| joyzepam | μ31 | μ32 | |
| total |
Okay, what about the remaining entries? For instance, how should we describe the average mood gain across the entire (hypothetical) population of people who might be given Joyzepam in an experiment like this, regardless of whether they were in CBT? We use the “dot” notation to express this. In the case of Joyzepam, notice that we’re talking about the mean associated with the third row in the table. That is, we’re averaging across two cell means (i.e., μ31 and μ32). The result of this averaging is referred to as a marginal mean, and would be denoted μ3. in this case. The marginal mean for CBT corresponds to the population mean associated with the second column in the table, so we use the notation μ.2 to describe it. The grand mean is denoted μ.. because it is the mean obtained by averaging (marginalising232) over both. So our full table of population means can be written down like this:
knitr::kable(tibble::tribble(
~V1, ~V2, ~V3, ~V4,
"placebo", "$\\mu_{11}$", "$\\mu_{12}$", "$\\mu_{1.}$",
"anxifree", "$\\mu_{21}$", "$\\mu_{22}$", "$\\mu_{2.}$",
"joyzepam", "$\\mu_{31}$", "$\\mu_{32}$", "$\\mu_{3.}$",
"total", "$\\mu_{.1}$", "$\\mu_{.2}$", "$\\mu_{..}$"
), col.names=c( NA, "no therapy", "CBT", "total"))| NA | no therapy | CBT | total |
|---|---|---|---|
| placebo | μ11 | μ12 | μ1. |
| anxifree | μ21 | μ22 | μ2. |
| joyzepam | μ31 | μ32 | μ3. |
| total | μ.1 | μ.2 | μ.. |
Now that we have this notation, it is straightforward to formulate and express some hypotheses. Let’s suppose that the goal is to find out two things: firstly, does the choice of drug have any effect on mood, and secondly, does CBT have any effect on mood? These aren’t the only hypotheses that we could formulate of course, and we’ll see a really important example of a different kind of hypothesis in Section 16.2, but these are the two simplest hypotheses to test, and so we’ll start there. Consider the first test. If drug has no effect, then we would expect all of the row means to be identical, right? So that’s our null hypothesis. On the other hand, if the drug does matter then we should expect these row means to be different. Formally, we write down our null and alternative hypotheses in terms of the equality of marginal means:
knitr::kable(tibble::tribble(
~V1, ~V2,
"Null hypothesis $H_0$:", "row means are the same i.e. $\\mu_{1.} = \\mu_{2.} = \\mu_{3.}$",
"Alternative hypothesis $H_1$:", "at least one row mean is different."
), col.names = c("", ""))| Null hypothesis H0: | row means are the same i.e. μ1.=μ2.=μ3. |
| Alternative hypothesis H1: | at least one row mean is different. |
It’s worth noting that these are exactly the same statistical hypotheses that we formed when we ran a one-way ANOVA on these data back in Chapter 14. Back then I used the notation μP to refer to the mean mood gain for the placebo group, with μA and μJ corresponding to the group means for the two drugs, and the null hypothesis was μP=μA=μJ. So we’re actually talking about the same hypothesis: it’s just that the more complicated ANOVA requires more careful notation due to the presence of multiple grouping variables, so we’re now referring to this hypothesis as μ1.=μ2.=μ3.. However, as we’ll see shortly, although the hypothesis is identical, the test of that hypothesis is subtly different due to the fact that we’re now acknowledging the existence of the second grouping variable.
Speaking of the other grouping variable, you won’t be surprised to discover that our second hypothesis test is formulated the same way. However, since we’re talking about the psychological therapy rather than drugs, our null hypothesis now corresponds to the equality of the column means:
knitr::kable(tibble::tribble(
~V1, ~V2,
"Null hypothesis $H_0$:", "column means are the same, i.e., $\\mu_{.1} = \\mu_{.2}$",
"Alternative hypothesis $H_1$:", "column means are different, i.e., $\\mu_{.1} \\neq \\mu_{.2}"
), col.names = c("", ""))| Null hypothesis H0: | column means are the same, i.e., μ.1=μ.2 |
| Alternative hypothesis H1: | column means are different, i.e., ${.1} {.2} |
Running the analysis in R
The null and alternative hypotheses that I described in the last section should seem awfully familiar: they’re basically the same as the hypotheses that we were testing in our simpler one-way ANOVAs in Chapter 14. So you’re probably expecting that the hypothesis tests that are used in factorial ANOVA will be essentially the same as the F-test from Chapter 14. You’re expecting to see references to sums of squares (SS), mean squares (MS), degrees of freedom (df), and finally an F-statistic that we can convert into a p-value, right? Well, you’re absolutely and completely right. So much so that I’m going to depart from my usual approach. Throughout this book, I’ve generally taken the approach of describing the logic (and to an extent the mathematics) that underpins a particular analysis first; and only then introducing the R commands that you’d use to produce the analysis. This time I’m going to do it the other way around, and show you the R commands first. The reason for doing this is that I want to highlight the similarities between the simple one-way ANOVA tool that we discussed in Chapter 14, and the more complicated tools that we’re going to use in this chapter.
If the data you’re trying to analyse correspond to a balanced factorial design, then running your analysis of variance is easy. To see how easy it is, let’s start by reproducing the original analysis from Chapter 14. In case you’ve forgotten, for that analysis we were using only a single factor (i.e., drug) to predict our outcome variable (i.e., mood.gain), and so this was what we did:
model.1 <- aov( mood.gain ~ drug, clin.trial )
summary( model.1 ) ## Df Sum Sq Mean Sq F value Pr(>F)
## drug 2 3.453 1.7267 18.61 8.65e-05 ***
## Residuals 15 1.392 0.0928
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Note that this time around I’ve used the name model.1 as the label for my aov object, since I’m planning on creating quite a few other models too. To start with, suppose I’m also curious to find out if therapy has a relationship to mood.gain. In light of what we’ve seen from our discussion of multiple regression in Chapter 15, you probably won’t be surprised that all we have to do is extend the formula: in other words, if we specify mood.gain ~ drug + therapy as our model, we’ll probably get what we’re after:
model.2 <- aov( mood.gain ~ drug + therapy, clin.trial ) This output is pretty simple to read too: the first row of the table reports a between-group sum of squares (SS) value associated with the drug factor, along with a corresponding between-group df value. It also calculates a mean square value (MS), and F-statistic and a p-value. There is also a row corresponding to the therapy factor, and a row corresponding to the residuals (i.e., the within groups variation).
Not only are all of the individual quantities pretty familiar, the relationships between these different quantities has remained unchanged: just like we saw with the original one-way ANOVA, note that the mean square value is calculated by dividing SS by the corresponding df. That is, it’s still true that
\(\ MS = {SS \over df}\)
regardless of whether we’re talking about drug, therapy or the residuals. To see this, let’s not worry about how the sums of squares values are calculated: instead, let’s take it on faith that R has calculated the SS values correctly, and try to verify that all the rest of the numbers make sense. First, note that for the drug factor, we divide 3.45 by 2, and end up with a mean square value of 1.73. For the therapy factor, there’s only 1 degree of freedom, so our calculations are even simpler: dividing 0.47 (the SS value) by 1 gives us an answer of 0.47 (the MS value).
Turning to the F statistics and the p values, notice that we have two of each: one corresponding to the drug factor and the other corresponding to the therapy factor. Regardless of which one we’re talking about, the F statistic is calculated by dividing the mean square value associated with the factor by the mean square value associated with the residuals. If we use “A” as shorthand notation to refer to the first factor (factor A; in this case drug) and “R” as shorthand notation to refer to the residuals, then the F statistic associated with factor A is denoted FA, and is calculated as follows:
\(\ F_A={MS_A \over MS_R}\)
and an equivalent formula exists for factor B (i.e., therapy). Note that this use of “R” to refer to residuals is a bit awkward, since we also used the letter R to refer to the number of rows in the table, but I’m only going to use “R” to mean residuals in the context of SSR and MSR, so hopefully this shouldn’t be confusing. Anyway, to apply this formula to the drugs factor, we take the mean square of 1.73 and divide it by the residual mean square value of 0.07, which gives us an F-statistic of 26.15. The corresponding calculation for the therapy variable would be to divide 0.47 by 0.07 which gives 7.08 as the F-statistic. Not surprisingly, of course, these are the same values that R has reported in the ANOVA table above.
The last part of the ANOVA table is the calculation of the p values. Once again, there is nothing new here: for each of our two factors, what we’re trying to do is test the null hypothesis that there is no relationship between the factor and the outcome variable (I’ll be a bit more precise about this later on). To that end, we’ve (apparently) followed a similar strategy that we did in the one way ANOVA, and have calculated an F-statistic for each of these hypotheses. To convert these to p values, all we need to do is note that the that the sampling distribution for the F statistic under the null hypothesis (that the factor in question is irrelevant) is an F distribution: and that two degrees of freedom values are those corresponding to the factor, and those corresponding to the residuals. For the drug factor we’re talking about an F distribution with 2 and 14 degrees of freedom (I’ll discuss degrees of freedom in more detail later). In contrast, for the therapy factor sampling distribution is F with 1 and 14 degrees of freedom. If we really wanted to, we could calculate the p value ourselves using the pf() function (see Section 9.6). Just to prove that there’s nothing funny going on, here’s what that would look like for the drug variable:
pf( q=26.15, df1=2, df2=14, lower.tail=FALSE )## [1] 1.871981e-05And as you can see, this is indeed the p value reported in the ANOVA table above.
At this point, I hope you can see that the ANOVA table for this more complicated analysis corresponding to model.2 should be read in much the same way as the ANOVA table for the simpler analysis for model.1. In short, it’s telling us that the factorial ANOVA for our 3×2 design found a significant effect of drug (F2,14=26.15,p<.001) as well as a significant effect of therapy (F1,14=7.08,p=.02). Or, to use the more technically correct terminology, we would say that there are two main effects of drug and therapy. At the moment, it probably seems a bit redundant to refer to these as “main” effects: but it actually does make sense. Later on, we’re going to want to talk about the possibility of “interactions” between the two factors, and so we generally make a distinction between main effects and interaction effects.
the sum of squares calculated?
In the previous section I had two goals: firstly, to show you that the R commands needed to do factorial ANOVA are pretty much the same ones that we used for a one way ANOVA. The only difference is the formula argument to the aov() function. Secondly, I wanted to show you what the ANOVA table looks like in this case, so that you can see from the outset that the basic logic and structure behind factorial ANOVA is the same as that which underpins one way ANOVA. Try to hold onto that feeling. It’s genuinely true, insofar as factorial ANOVA is built in more or less the same way as the simpler one-way ANOVA model. It’s just that this feeling of familiarity starts to evaporate once you start digging into the details. Traditionally, this comforting sensation is replaced by an urge to murder the the authors of statistics textbooks.
Okay, let’s start looking at some of those details. The explanation that I gave in the last section illustrates the fact that the hypothesis tests for the main effects (of drug and therapy in this case) are F-tests, but what it doesn’t do is show you how the sum of squares (SS) values are calculated. Nor does it tell you explicitly how to calculate degrees of freedom (df values) though that’s a simple thing by comparison. Let’s assume for now that we have only two predictor variables, Factor A and Factor B. If we use Y to refer to the outcome variable, then we would use Yrci to refer to the outcome associated with the i-th member of group rc (i.e., level/row r for Factor A and level/column c for Factor B). Thus, if we use \(\ \bar{Y}\) to refer to a sample mean, we can use the same notation as before to refer to group means, marginal means and grand means: that is, \(\ \bar{Y_{rc}}\) is the sample mean associated with the rth level of Factor A and the cth level of Factor B, \(\ \bar{Y_r}\). would be the marginal mean for the rth level of Factor A, \(\ \bar{Y_{.c}}\) would be the marginal mean for the cth level of Factor B, and \(\ \bar{Y_{..}}\) is the grand mean. In other words, our sample means can be organised into the same table as the population means. For our clinical trial data, that table looks like this:
knitr::kable(tibble::tribble(
~V1, ~V2, ~V3, ~V4,
"placebo", "$\\bar{Y}_{11}$", "$\\bar{Y}_{12}$", "$\\bar{Y}_{1.}$",
"anxifree", "$\\bar{Y}_{21}$", "$\\bar{Y}_{22}$", "$\\bar{Y}_{2.}$",
"joyzepam", "$\\bar{Y}_{31}$", "$\\bar{Y}_{32}$", "$\\bar{Y}_{3.}$",
"total", "$\\bar{Y}_{.1}$", "$\\bar{Y}_{.2}$", "$\\bar{Y}_{..}$"
), col.names = c("", "no therapy", "CBT", "total"))| no therapy | CBT | total | |
|---|---|---|---|
| placebo | \(\ \bar{Y_{11}}\) | \(\ \bar{Y_{12}}\) | \(\ \bar{Y_{1.}}\) |
| anxifree | \(\ \bar{Y_{21}}\) | \(\ \bar{Y_{22}}\) | \(\ \bar{Y_{2.}}\) |
| joyzepam | \(\ \bar{Y_{31}}\) | \(\ \bar{Y_{32}}\) | \(\ \bar{Y_{3.}}\) |
| total | \(\ \bar{Y_{.1}}\) | \(\ \bar{Y_{.2}}\) | \(\ \bar{Y_{..}}\) |
And if we look at the sample means that I showed earlier, we have \(\ \bar{Y_{11}}\) =0.30, \(\ \bar{Y_{12}}\)=0.60 etc. In our clinical trial example, the drugs factor has 3 levels and the therapy factor has 2 levels, and so what we’re trying to run is a 3×2 factorial ANOVA. However, we’ll be a little more general and say that Factor A (the row factor) has R levels and Factor B (the column factor) has C levels, and so what we’re runnning here is an R×C factorial ANOVA.
Now that we’ve got our notation straight, we can compute the sum of squares values for each of the two factors in a relatively familiar way. For Factor A, our between group sum of squares is calculated by assessing the extent to which the (row) marginal means \(\ \bar{Y_{1.}}\), \(\ \bar{Y_{2.}}\) etc, are different from the grand mean \(\ \bar{Y_{..}}\). We do this in the same way that we did for one-way ANOVA: calculate the sum of squared difference between the \(\ \bar{Y_{i.}}\) values and the \(\ \bar{Y_{..}}\) values. Specifically, if there are N people in each group, then we calculate this:
\(\ SS_A=(N \times C) \sum_{r=1}^R(\bar{Y_{r.}} - \bar{Y_{..}})^2\)
As with one-way ANOVA, the most interesting233 part of this formula is the \(\ (\bar{Y_{r.}} - \bar{Y_{..}})^2\) bit, which corresponds to the squared deviation associated with level r. All that this formula does is calculate this squared deviation for all R levels of the factor, add them up, and then multiply the result by N×C. The reason for this last part is that there are multiple cells in our design that have level r on Factor A: in fact, there are C of them, one corresponding to each possible level of Factor B! For instance, in our toy example, there are two different cells in the design corresponding to the anxifree drug: one for people with no.therapy, and one for the CBT group. Not only that, within each of these cells there are N observations. So, if we want to convert our SS value into a quantity that calculates the between-groups sum of squares on a “per observation” basis, we have to multiply by by N×C. The formula for factor B is of course the same thing, just with some subscripts shuffled around:
\(\ SS_B = (N \times R)\sum_{c=1}^C(\bar{Y_{.c}} - \bar{Y_{..}})^2\)
Now that we have these formulas, we can check them against the R output from the earlier section. First, notice that we calculated all the marginal means (i.e., row marginal means \(\ \bar{Y_{r.}}\) and column marginal means \(\ \bar{Y_{.c}}\)) earlier using aggregate(), and we also calculated the grand mean. Let’s repeat those calculations, but this time we’ll save the results to varibles so that we can use them in subsequent calculations:
drug.means <- aggregate( mood.gain ~ drug, clin.trial, mean )[,2]
therapy.means <- aggregate( mood.gain ~ therapy, clin.trial, mean )[,2]
grand.mean <- mean( clin.trial$mood.gain )Okay, now let’s calculate the sum of squares associated with the main effect of drug. There are a total of N=3 people in each group, and C=2 different types of therapy. Or, to put it another way, there are 3×2=6 people who received any particular drug. So our calculations are:
SS.drug <- (3*2) * sum( (drug.means - grand.mean)^2 )
SS.drug## [1] 3.453333Not surprisingly, this is the same number that you get when you look up the SS value for the drugs factor in the ANOVA table that I presented earlier. We can repeat the same kind of calculation for the effect of therapy. Again there are N=3 people in each group, but since there are R=3 different drugs, this time around we note that there are 3×3=9 people who received CBT, and an additional 9 people who received the placebo. So our calculation is now:
SS.therapy <- (3*3) * sum( (therapy.means - grand.mean)^2 )
SS.therapy## [1] 0.4672222and we are, once again, unsurprised to see that our calculations are identical to the ANOVA output.
So that’s how you calculate the SS values for the two main effects. These SS values are analogous to the between-group sum of squares values that we calculated when doing one-way ANOVA in Chapter 14. However, it’s not a good idea to think of them as between-groups SS values anymore, just because we have two different grouping variables and it’s easy to get confused. In order to construct an F test, however, we also need to calculate the within-groups sum of squares. In keeping with the terminology that we used in the regression chapter (Chapter 15) and the terminology that R uses when printing out the ANOVA table, I’ll start referring to the within-groups SS value as the residual sum of squares SSR.
The easiest way to think about the residual SS values in this context, I think, is to think of it as the leftover variation in the outcome variable after you take into account the differences in the marginal means (i.e., after you remove SSA and SSB). What I mean by that is we can start by calculating the total sum of squares, which I’ll label SST. The formula for this is pretty much the same as it was for one-way ANOVA: we take the difference between each observation Yrci and the grand mean \(\ \bar{Y_{..}}\), square the differences, and add them all up
\(\ SS_T=\sum_{r=1}^R\sum_{c=1}^C\sum_{i=1}^N(Y_{rci} - \bar{Y_{..}})^2\)
The “triple summation” here looks more complicated than it is. In the first two summations, we’re summing across all levels of Factor A (i.e., over all possible rows r in our table), across all levels of Factor B (i.e., all possible columns c). Each rc combination corresponds to a single group, and each group contains N people: so we have to sum across all those people (i.e., all i values) too. In other words, all we’re doing here is summing across all observations in the data set (i.e., all possible rci combinations).
At this point, we know the total variability of the outcome variable SST, and we know how much of that variability can be attributed to Factor A (SSA) and how much of it can be attributed to Factor B (SSB). The residual sum of squares is thus defined to be the variability in Y that can’t be attributed to either of our two factors. In other words:
SSR=SST − (SSA+SSB)
Of course, there is a formula that you can use to calculate the residual SS directly, but I think that it makes more conceptual sense to think of it like this. The whole point of calling it a residual is that it’s the leftover variation, and the formula above makes that clear. I should also note that, in keeping with the terminology used in the regression chapter, it is commonplace to refer to SSA+SSB as the variance attributable to the “ANOVA model”, denoted SSM, and so we often say that the total sum of squares is equal to the model sum of squares plus the residual sum of squares. Later on in this chapter we’ll see that this isn’t just a surface similarity: ANOVA and regression are actually the same thing under the hood.
In any case, it’s probably worth taking a moment to check that we can calculate SSR using this formula, and verify that we do obtain the same answer that R produces in its ANOVA table. The calculations are pretty straightforward. First we calculate the total sum of squares:
SS.tot <- sum( (clin.trial$mood.gain - grand.mean)^2 )
SS.tot## [1] 4.845and then we use it to calculate the residual sum of squares:
SS.res <- SS.tot - (SS.drug + SS.therapy)
SS.res## [1] 0.9244444Yet again, we get the same answer.
What are our degrees of freedom?
The degrees of freedom are calculated in much the same way as for one-way ANOVA. For any given factor, the degrees of freedom is equal to the number of levels minus 1 (i.e., R−1 for the row variable, Factor A, and C−1 for the column variable, Factor B). So, for the drugs factor we obtain df=2, and for the therapy factor we obtain df=1. Later on on, when we discuss the interpretation of ANOVA as a regression model (see Section 16.6) I’ll give a clearer statement of how we arrive at this number, but for the moment we can use the simple definition of degrees of freedom, namely that the degrees of freedom equals the number of quantities that are observed, minus the number of constraints. So, for the drugs factor, we observe 3 separate group means, but these are constrained by 1 grand mean; and therefore the degrees of freedom is 2. For the residuals, the logic is similar, but not quite the same. The total number of observations in our experiment is 18. The constraints correspond to the 1 grand mean, the 2 additional group means that the drug factor introduces, and the 1 additional group mean that the the therapy factor introduces, and so our degrees of freedom is 14. As a formula, this is N−1−(R−1)−(C−1), which simplifies to N−R−C+1.
Factorial ANOVA versus one-way ANOVAs
Now that we’ve seen how a factorial ANOVA works, it’s worth taking a moment to compare it to the results of the one way analyses, because this will give us a really good sense of why it’s a good idea to run the factorial ANOVA. In Chapter 14 that I ran a one-way ANOVA that looked to see if there are any differences between drugs, and a second one-way ANOVA to see if there were any differences between therapies. As we saw in Section 16.1.1, the null and alternative hypotheses tested by the one-way ANOVAs are in fact identical to the hypotheses tested by the factorial ANOVA. Looking even more carefully at the ANOVA tables, we can see that the sum of squares associated with the factors are identical in the two different analyses (3.45 for drug and 0.92 for therapy), as are the degrees of freedom (2 for drug, 1 for therapy). But they don’t give the same answers! Most notably, when we ran the one-way ANOVA for therapy in Section 14.11 we didn’t find a significant effect (the p-value was 0.21). However, when we look at the main effect of therapy within the context of the two-way ANOVA, we do get a significant effect (p=.019). The two analyses are clearly not the same.
Why does that happen? The answer lies in understanding how the residuals are calculated. Recall that the whole idea behind an F-test is to compare the variability that can be attributed to a particular factor with the variability that cannot be accounted for (the residuals). If you run a one-way ANOVA for therapy, and therefore ignore the effect of drug, the ANOVA will end up dumping all of the drug-induced variability into the residuals! This has the effect of making the data look more noisy than they really are, and the effect of therapy which is correctly found to be significant in the two-way ANOVA now becomes non-significant. If we ignore something that actually matters (e.g., drug) when trying to assess the contribution of something else (e.g., therapy) then our analysis will be distorted. Of course, it’s perfectly okay to ignore variables that are genuinely irrelevant to the phenomenon of interest: if we had recorded the colour of the walls, and that turned out to be non-significant in a three-way ANOVA (i.e. mood.gain ~ drug + therapy + wall.colour), it would be perfectly okay to disregard it and just report the simpler two-way ANOVA that doesn’t include this irrelevant factor. What you shouldn’t do is drop variables that actually make a difference!
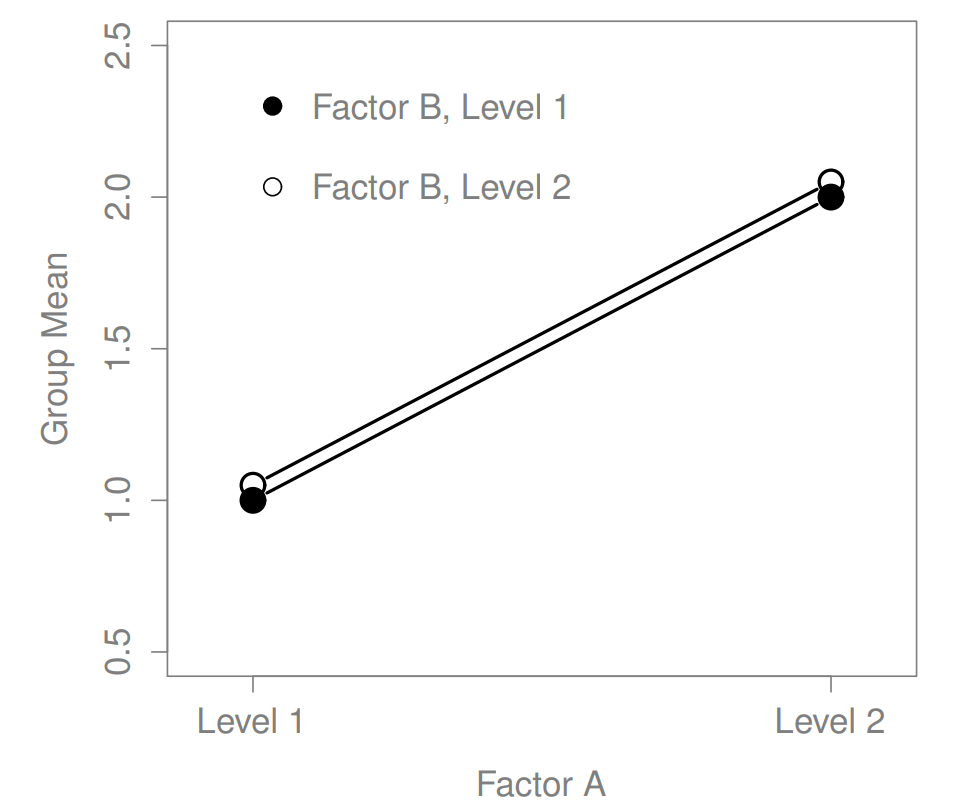
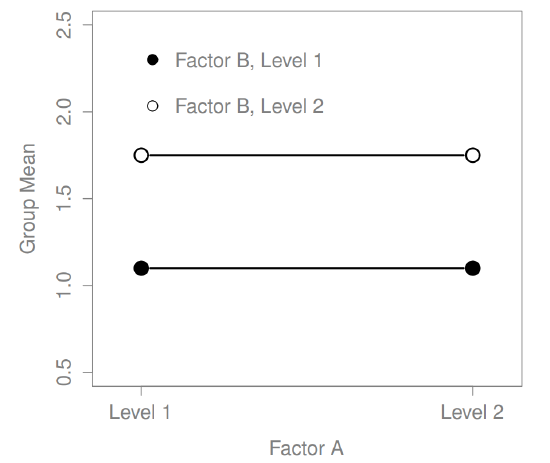
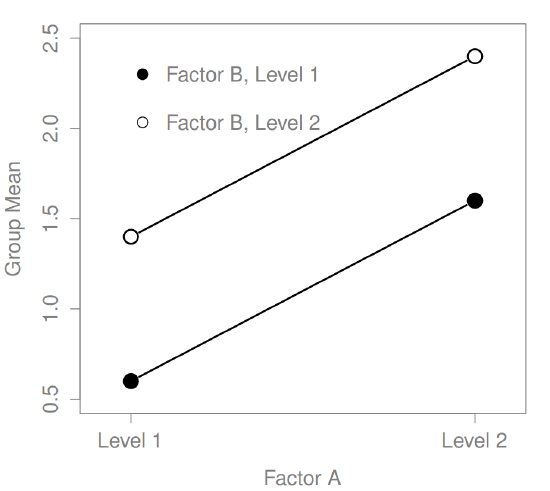
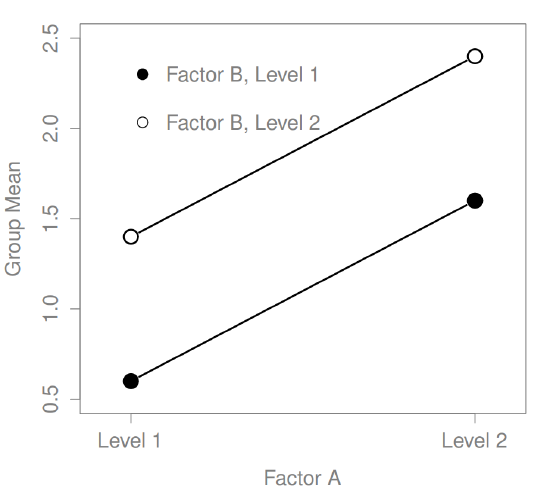
What kinds of outcomes does this analysis capture?
The ANOVA model that we’ve been talking about so far covers a range of different patterns that we might observe in our data. For instance, in a two-way ANOVA design, there are four possibilities: (a) only Factor A matters, (b) only Factor B matters, (c) both A and B matter, and (d) neither A nor B matters. An example of each of these four possibilities is plotted in Figure ??.


